力扣AC：下降路径最小和 - 路径问题

题目链接

下降路径最小和

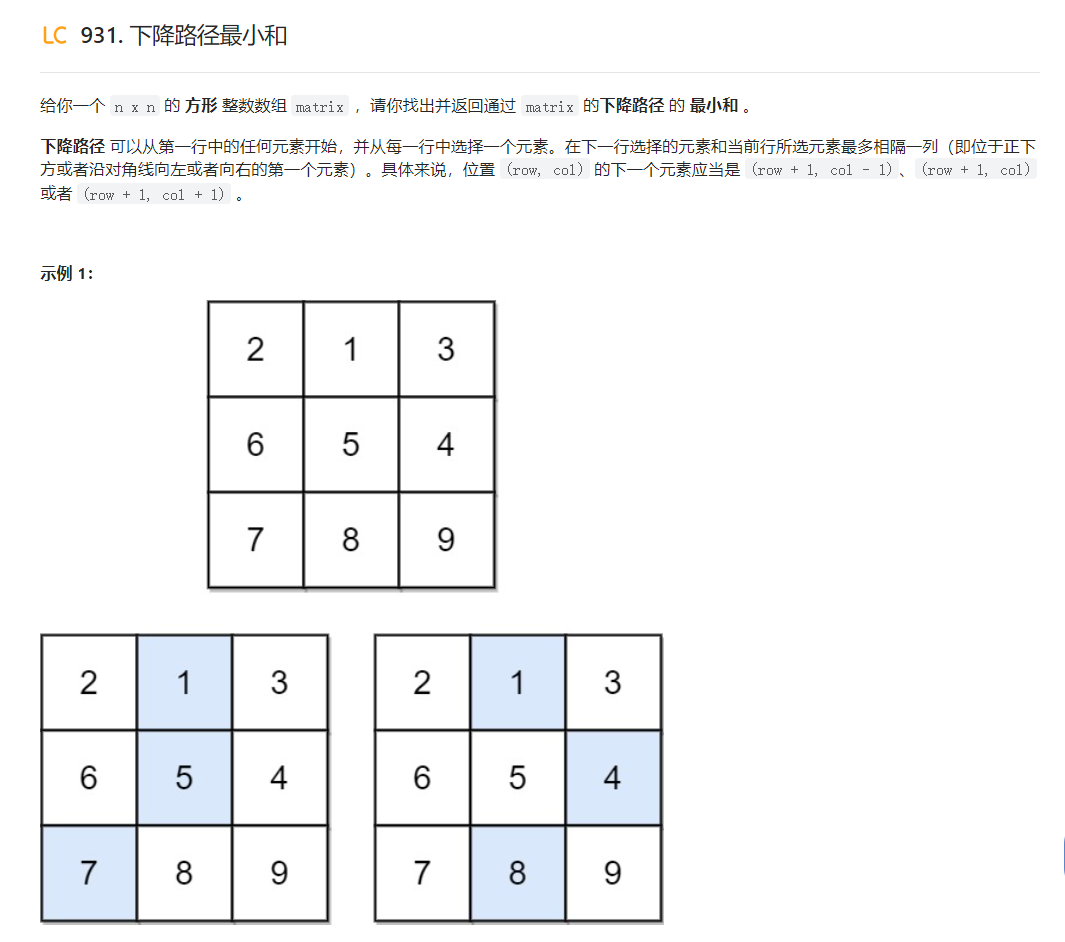
题目描述

实现代码

动态规划思想：记dp[i][j]为到达(i,j)位置的下降路径最小和，首先初始化条件：

1. dp[0][j] = matrix[0][j]

状态转移方程考虑三种情况：

1. j == 0时：dp[i][j] = max(dp[i-1][j], dp[i-1][j+1]) + matrix[i][j]
2. j == n-1时：dp[i][j] = max(dp[i-1][j-1], dp[i-1][j]) + matrix[i][j]
3. 其他情况时：dp[i][j] = max(dp[i-1][j-1], dp[i-1][j], dp[i-1][j+1]) + matrix[i][j]

实现代码：

class Solution {
    public int minFallingPathSum(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] dp = new int[m][n];
        int min = 10001;
        for (int j = 0; j < n; j++) {
            dp[0][j] = matrix[0][j];
            min = Math.min(min, dp[0][j]);
        }
        if(m == 1) {
            return min;
        }
        min = 10001;
        for (int i = 1; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (j == 0) {
                    dp[i][j] = Math.min(dp[i - 1][j], dp[i - 1][j + 1]) + matrix[i][j];
                } else if (j == n - 1) {
                    dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + matrix[i][j];
                } else {
                    dp[i][j] = Math.min(Math.min(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]) + matrix[i][j];
                }
                min = (i == m - 1 ? Math.min(min, dp[i][j]) : min);
            }
        }
        return min;
    }
}

二维数组的基础上进行一维数组降维优化，实现代码：

public int minFallingPathSum(int[][] matrix) {
        int n = matrix.length;
        int dp[] = new int[n];
        int ans = Integer.MAX_VALUE;
        for(int i = 0;i < n;i++){
            int pre = 0;
            for(int j = 0;j < n;j++){
                int num = matrix[i][j];
                int tmp = dp[j];
                if(i == 0) dp[j] = num;
                else if(j == 0) dp[j] = Math.min(dp[j],dp[j+1])+num;
                else if(j == n-1) dp[j] = Math.min(dp[j],pre)+num;
                else dp[j] = Math.min(pre,Math.min(dp[j+1],dp[j]))+num;
                if(i == n-1){
                    ans = Math.min(ans,dp[j]);
                }
                pre = tmp;
            }
        }
        return ans;
    }