🚚引子-完全二叉树与堆结构;
完全二叉树
:::info
- 每层要么是满的,要么是左边先满右面再满
数组从0位置出发的连续一段,可以组成完全二叉树; :::
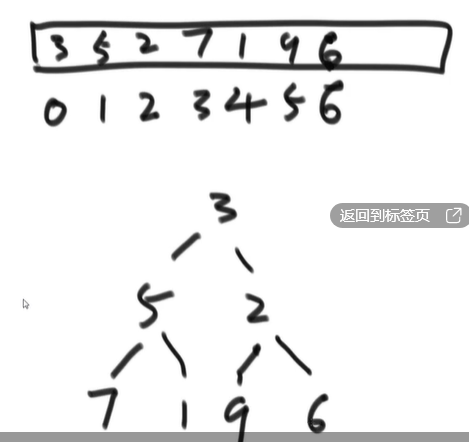
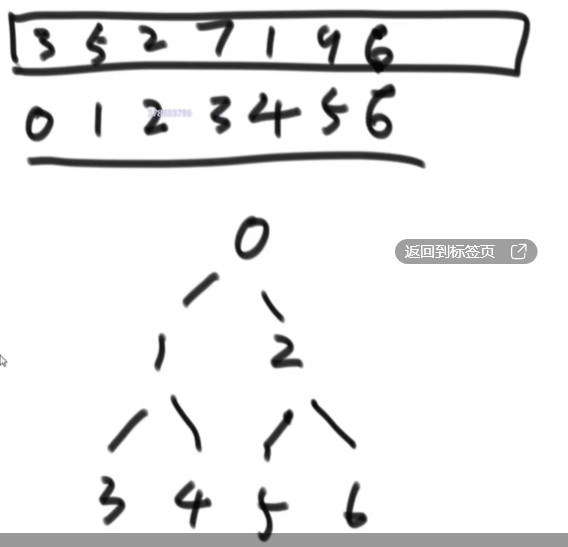
数组<=>完全二叉树 :::info 位置i:left child:2*i+1
- right child:2*i+2
- father: (i-1)/2
和满二叉树的性质有关;N节点的满二叉树,最后一行有(N)/2个节点; :::
堆
堆是一种完全二叉树,可以分为大根堆和小根堆;
:::info
大根堆:对于每一个子堆,根节点的值都是最大的;
小根堆:与大根堆相反;
:::
堆结构中最重要的操作是heapinsert和heapify;通过这两种操作可以将数组转化成大根堆或者小根堆;
heapinsert
:::info
- 每次加入一个数,要先和其父节点比较,
- 若是比父节点大,则交换,并且将当前节点变成此节点;
- 直到遇到比插入的数要大的父节点或是到根节点;
:::
:::tips 可以通过上述操作看出大根堆的最大值在堆顶void heapInsert(vector<int> &vec, int index){//插入的数在index位置;假设index之前的数已经形成堆了;while(vec[index]>vec[(index-1)>>1]){swap(vec,index,(index-1)>>1);index=(index-1)>>1;}}
heapinsert操作主要是对堆某节点的上游节点操作; :::
heapify
若是要求删除堆顶,并将最后位置的数放在堆顶位置;
若是改变了某位置的数,如何重新变成堆?
void heapify(vector<int> &vec,int index,int heapSize ){//index 表示从哪里开始做heapifyint left=index*2+1;while(left<heapSize){//当仍然有child时int largest=left+1<heapSize&&vec[left+1]>vec[left]?left+1:left;//判定right child 存,largest取left和right中较大的那个largest=vec[largest]>vec[index]?largest:index;//largest取father和child中较大的那个if(largest==index)break;swap(vec,largest,index);index=largest;left=index*2+1;}}
:::info
heapify操作后,该数组会变成合法的堆吗?
不一定,若是之前已经成堆了,可以;否则不一定。
:::
:::tips
heapify操作主要是对堆的下游节点进行比对
至此,堆结构中两个最重要的操作已经建立
- 想要将一个数组变成堆:对于所有位置依次进行heapInsert
heapinsert是向上进行的,和上层的数据油管
heapify是向下进行的,和下层的数据油管;
若是将堆中任意位置的数据改变了;
- 变小了->向下经历一个heapify,将child中的大值顶上来
- 变大了->向上经历一个heapinsert,把此值顶替到根节点; :::
:::success
调整的复杂度:
因为高度是log N级别;而调整一般都是沿着高度进行的,所以时间复杂度是:
:::
堆排序
:::info 解析:
- 将数组变成堆 heapinsert
- 堆顶与堆尾部的数交换,数组末尾即为当前堆的最大值
- heapsize—
- heapify
- 重复2-4知道heapsize=0;
:::
时间复杂度void heapSort(vector<int> &vec){if(vec.size()<2) return;for(int i=0;i<vec.size();i++){\\变成heap;heapInsert(vec,i);}int heapsize=vec.size();while(heapsize>0){swap(vec,0,heapsize);heapify(vec,0,--heapsize);}}
额外的空间复杂度
复杂度更低的heapinsert
若是一开始给出了所有的数据,可以不按照从上往下做heapinsert,而是从下往上做heapify
复杂度
for(int i=vec.size()-1;i>=0;i--){heapify(vec,i,vec.size());}
题目
 :::info
解析:
:::info
解析:
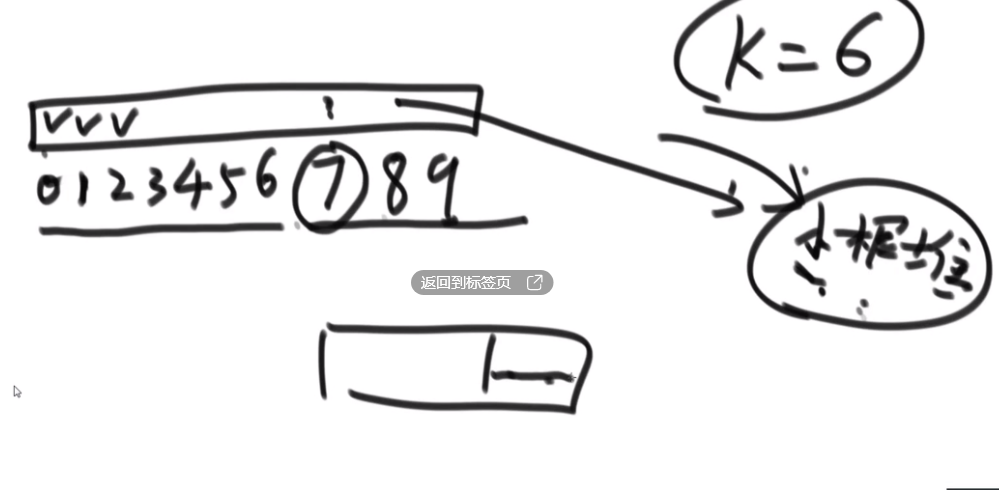
若是采用暴力搜索,复杂度必然是O(N^2)
每个元素移动距离不超过k,假设是从小到大排序,从0到6的7个元素生成一个小根堆,那么堆顶必然是整个数组中最小的元素。之后将下一个数加入,对1-7生成堆(heapinsert)
:::
 :::tips
:::tips
- 0-K生成一个小根堆(heapify)
- 弹出堆顶,将其换成下一个数,然后heapify
将数组中所有数加入后,依次弹出堆顶,并在生成堆; :::
void heapInsert(vector<int> &vec, int index);void heapify(vector<int> &vec,int index,int heapSize);void KheapSort(vector<int> &vec,int K){vector<int> temp;int index=0;for(;index<min(temp.size(),K+1);index++){heapinsert(temp,index);}int i=0;for(;i<temp.size(),index<temp.size();i++,index++){vec[i]=temp[0];temp[0]=temp[index];heapify(temp,0,K+1)}for(;i<temp.size();i++){vec[i]=temp[0];temp[0]=temp[K--];heapify(temp,0;K+1);}}
实际上C++中自带堆结构:
(11条消息) c++重拾 STL之heap(堆)_元气满满晨-CSDN博客_c++ heap#include<algorithm>#include<vector>void KheapSort(vector<int> &vec,int K){K=K>vec.size()?vec.size()-1:K;vector<int> heap(vec.begin(),&vec[K]);make_heap(heap.begin(),heap.end(),less<int>());int index=K+1;int i=0;for(;index<vec.size();index++,i++){vec[i]=heap[0];pop_heap(heap.begin(),heap.end(),less<int>());heap.pop_back();heap.push_back(vec[index]);push_heap(heap.begin(),heap.end(),less<int>());}for(;i<vec.size();i++){vec[i]=heap[0];pop_heap(heap.begin(),heap.end(),less<int>());heap.pop_back();}}
桶排序
:::info 之前涉及的插入、归并、冒泡、快排序、堆排序等都是基于比较的排序 ::: 不基于比较的排序: :::success
e.g.统计员工的年龄
- 指定一个18-100的词频数组
- 出现一个相应年龄的便在相应位置++
- 最后将词频数组还原
复杂度
- 缺陷是词频表范围是有限or较小的 ::: 不基于比较的排序都是基于数据状况进行的,应用范围应该比基于比较的排序小
基数排序/桶排序
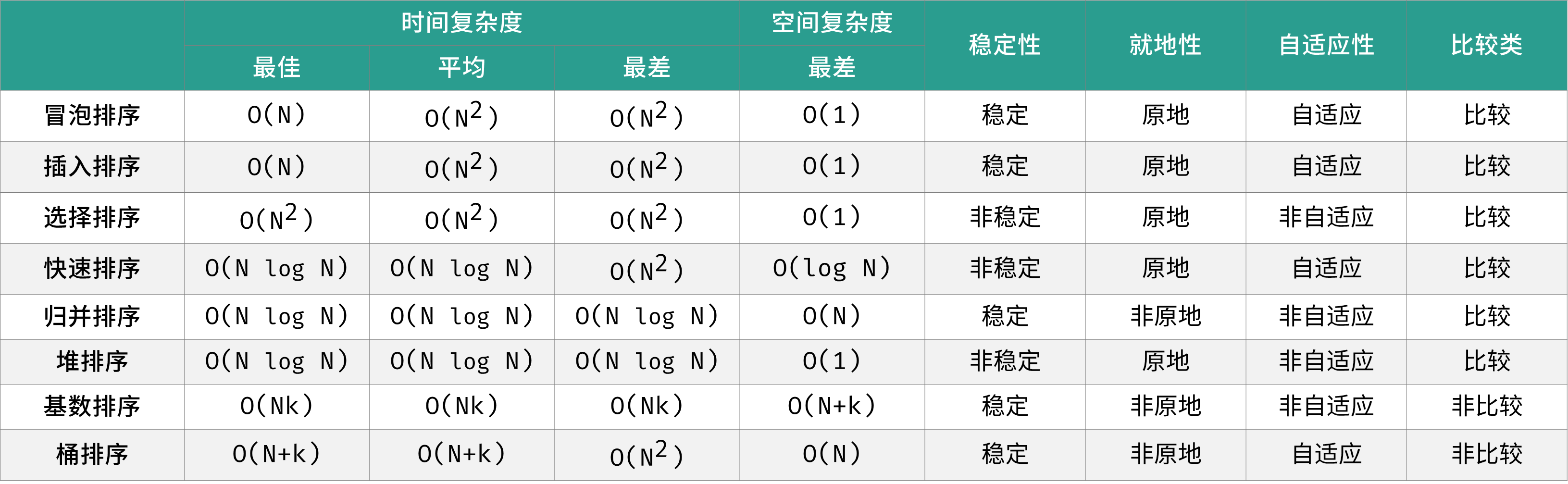
排序算法稳定性汇总
:::info 同样值的个体之间,若是不因为排序而改变相对次序,那么这个排序就是稳定的; ::: :::tips 不具备稳定性的排序:
- 选择排序
- 快速排序
- 堆排序
具备稳定性的排序:
- 冒泡排序
- 插入排序
- 归并排序
- 一切桶排序思想下的排序 :::
 :::tips
:::tips
- 基于比较的排序能否做到时间复杂度小于
?不能!
- 能否在此时间复杂度下,达到空间复杂度在
以下且稳定?不能! :::
常见的坑

常见改进
:::info
- 充分利用两种时间复杂度的排序的优势
稳定性的考虑 ::: 综合排序
小样本量时用插入排序
- 整体调度时用快排序
(动态的调用)
基础类型用快排,非基础类型用归并?why?稳定性问题

