时间复杂度

常数时间的操作

:::info 若是一个操作和数据量无关，即为常数时间的操作；
若是操作和数据量有关，则为线性时间的操作； ::: 例如：
数组中第i个数据的值：常数时间操作
取链表中第i个数据的值：线性时间操作（需要用指针不断寻址，需要的操作数随i变化）

选择排序复杂度分析

原理：前n个元素保持有序的，不断将后面的最小的元素加入前面的有序数列

void selectionSort(int &arr){
    for(int i=0;i<arr.size();i++){
        int minIndex=i;
        for(int j=i+1;j<n;j++){
            minIndex=arr[j]<arr[minIndex]?j:minIndex;
        }
        swap(arr[i],arr[minIndex]);
    }
}

分析： :::info

查看算是常数时间操作，比较一次也是，交换也是；
step 1：看 N次，比较N，交换1；
step 2：看 N-1次，比较N-1，交换1；
……
stepN-1…… ::: :::tips 一共发生了多少次：
看：N+N-1+N-2+……
比较：N+N-1+N-2……
交换：N
总计：aN^2+bN+C
时间复杂度： :::

Def 时间复杂度 :::success 常数时间操作次数和的表达式中最高阶项忽略系数

是一种上界（最坏情况） :::

冒泡排序

```cpp void bubbleSort(int &arr){ for(int e=arr.size();e>0;e—){

  for(int i=0;i<e;i++){
      if(arr[i]>arr[i+1])
          swap(arr[i],arr[i+1]);         
  }

} }

:::info
原理，大数像是气泡一样，每次最大的数会从底端上浮到顶端N；每次最后一个数都会变成有序的
:::
<a name="G8SLm"></a>
# *异或运算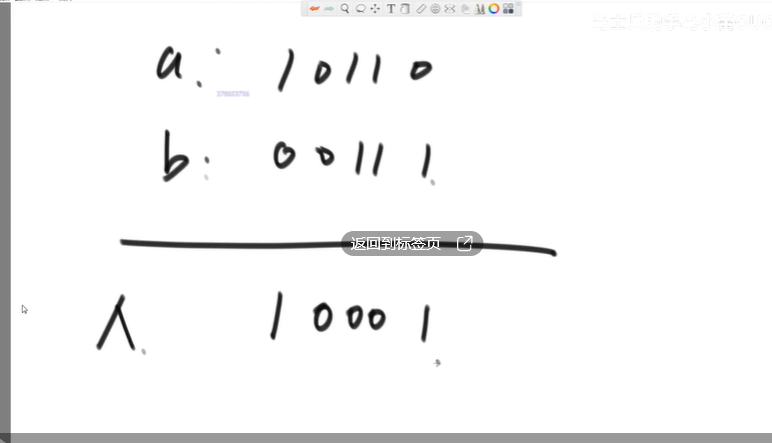
![d4165ad1-c29f-4c5f-a701-49161af3a156.png](https://cdn.nlark.com/yuque/0/2021/png/1303425/1638278340197-1dcc478d-ce09-4d23-aa46-aa347e172fe5.png#clientId=u11c2b99d-bf86-4&crop=0&crop=0&crop=1&crop=1&from=drop&height=255&id=u05f52c16&margin=%5Bobject%20Object%5D&name=d4165ad1-c29f-4c5f-a701-49161af3a156.png&originHeight=443&originWidth=772&originalType=binary&ratio=1&rotation=0&showTitle=false&size=48254&status=done&style=none&taskId=u3baee577-73f3-4c51-8ed5-18540a3ffb4&title=&width=445)
:::info
异或：相同为0，不同为1；或者理解为无进位相加；
:::
性质：
- 0^N=N;
- N^N=0;
- a^b=b^a;a^b^c=a^(b^c)交换律和结合律也满足
:::success
同一批数异或起来，和顺序无关；
- 理解起来可以从无进位相加来理解；
:::
<a name="Z3thq"></a>
## 异或实现交换
```cpp
void swap(int &a,int &b){
    a=a^b;//a=A^B,b=b
    b=a^b;//a=A^B,b=A^B^B=A^0=A;
    a=a^b;//a=A^B^A=B,b=A;
}

:::warning 需要保证ab是在内存中的两个不同的东西，否则会将该数变成0； :::

例题

:::info LeetCode136：
给定一个整数数组 nums，其中恰好有1个元素只出现一次，其余所有元素均出现两次。找出只出现一次的那1个元素 :::

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int eor=0;
        for(int i=0;i<nums.size();i++){
            eor=eor^nums[i];
        }
        return eor;
    }
};

:::tips 解析：要利用异或运算的交换律和结合律；
[a,b,c,a,b,c,c]异或等价于a^a^b^b^c^c^c=c; ::: Leecode 260：
若是存在2个数呢？ :::tips 解析：同样地将所有数异或一遍，得到的结果应该是a^b；
a和b至少应该有一位是不同的（因为a!=b），也就是这一位必然是1，则可以根据这一点区分；：

eor’只和该位不是1的数进行异或，得到的要么是a要么是b :::

class Solution {
public:
  int singleNumber(vector<int>& nums) {
      int eor=0;
      for(int i=0;i<nums.size();i++){
          eor=eor^nums[i];
      }
      int rightOne=eor&(~eor+1);//提取出最右边的1,惯用法
     /*eor 10110100
      ~eor 01001011
      +1   01001100
      +    00000100
      */
      int onlyOne=0;
      for(int i=0;i<nums.size();i++){
          if(nums[i]&rightOne==1)//!=0?这里存疑
            onlyOne=onlyOne^nums[i];
      }
      eor=eor^onlyOne;
  }
};

插入排序

:::info

复杂度
第i轮只保证前i个是有序的（i=0-N-1）
每轮最多执行i次交换，最多N-1轮
数据状况不同会导致算法复杂度的情况不一样，最差情况是我们需要衡量的 ::: :::tips 基本思想类似于打牌时摸牌，每次摸牌后把最小的牌放在最前面； :::
```
void insertionSort(vector<int> &vec){
    int num=vec.size();
  for(int i=1;i<num;i++){
    for(int j=i-1;j>=0;j--){
        if(vec[j]>vec[j+1])
        swap(vec[j],vec[j+1]);
    }
}
}
```
二分查找
:::tips 前提：有序数组（其实也不一定，只要有一定的条件、规律，都可以尝试？） ::: 复杂度
遍历：

二分： 🎈01_重新认识算法复杂度和排序算法 - 图4

从有序数组

int binSearch(vector<int>& vec;int e,int lo, int hi){//升序排列的数组
  while(lo<hi)
  {
      int mi=(lo+hi)>>1;
      if(e<vec[mi]){
          hi=mi;
      }else if(e>vec[mi]){
          lo=mi+1
      }else{
          return mi;
      }
  }
  return -1;
}

找大于某个数的最左侧位置

template <typename T> static Rank BinSearch (T * A, T const &e, Rank lo, Rank hi){
  while(lo<hi){//有效查找区间缩短到0时，才会停止
      Rank mi=(lo+hi)>>1;
      e<A[mi]?hi=mi:lo=mi+1;
  }//结束时，A[lo=mi]为大于e的最小元素
  return --lo;
}

局部最小问题

:::info 在无序数组A中，任何两个相邻数一定不相等；求局部最小
局部最小？

0<1: localmin=0
N-1<N-2:local=N-1

i-1<i<i+1：localmin=i; :::

int localMin(const vector<int> &A){
  int hi=A.size()-1;
  int lo=0;
  if(A[hi]<A[hi-1]) return A[hi];
  if(A[lo]<A[lo+1]) return A[lo];
  while(lo<hi){
      int mi=(lo+hi)>>1;
      if(A[mi]>A[mi-1]){
          hi=mi;
      }else if(A[mi]>A[mi]+1){
          lo=mi;
      }else{
          return A[mi];
      }
  }
}

:::tips 思路：相邻两数不相同，要么递增要么递减；
不一定非得数据有序才能二分；

要么数据特殊
要么问题特殊

构建出一种排他性 :::

关于二分法区间构造的两种情况

版本1

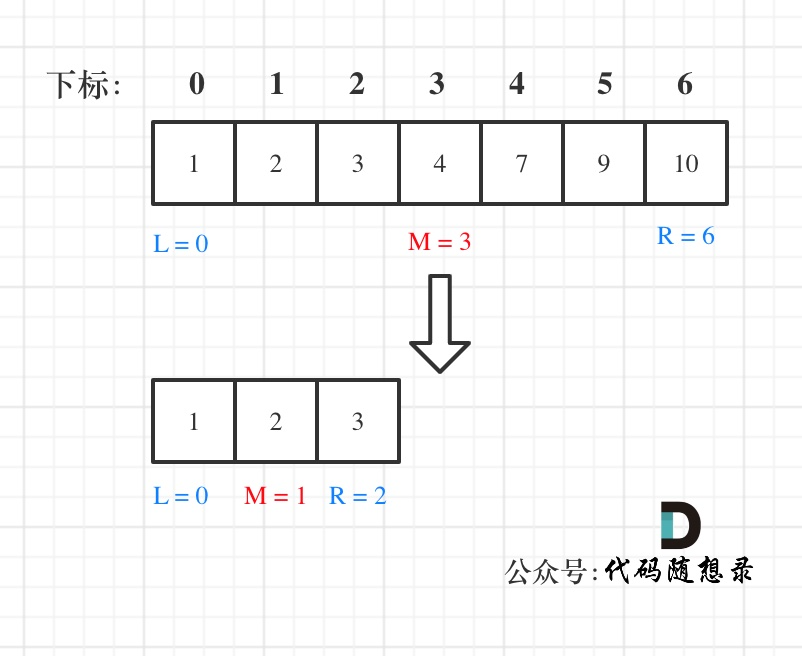
第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。
区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=

if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1 ```c class Solution { public: int search(vector& nums, int target) {

  int left = 0;
  int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
  while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
      int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
      if (nums[middle] > target) {
          right = middle - 1; // target 在左区间，所以[left, middle - 1]
      } else if (nums[middle] < target) {
          left = middle + 1; // target 在右区间，所以[middle + 1, right]
      } else { // nums[middle] == target
          return middle; // 数组中找到目标值，直接返回下标
      }
  }
  // 未找到目标值
  return -1;

} };

<a name="FKSyt"></a>
### 版本2
如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。<br />有如下两点：
- while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的
- if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]
```c
// 版本二
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};

🎈01_重新认识算法复杂度和排序算法