基本思想

:::info 动态规划的基本思想是通过转移方程遍历将当前状态转移；
求解动态规划的核心问题是穷举，只是在穷举过程中会有“备忘录”或是“DPtable”来进行剪枝。 ::: :::tips 1、确定 base case
2、确定「状态」，也就是原问题和子问题中会变化的变量。
3、确定「选择」，也就是导致「状态」产生变化的行为。
4、明确 dp 函数/数组的定义。
//————————————————————————————————————————————————————-

确定dp数组（dp table）以及下标的含义
确定递推公式
dp数组如何初始化
确定遍历顺序
举例推导dp数组 :::
```
# 初始化 base case
dp[0][0][...] = base
# 进行状态转移
for 状态1 in 状态1的所有取值：
 for 状态2 in 状态2的所有取值：
     for ...
         dp[状态1][状态2][...] = 求最值(选择1，选择2...)
```
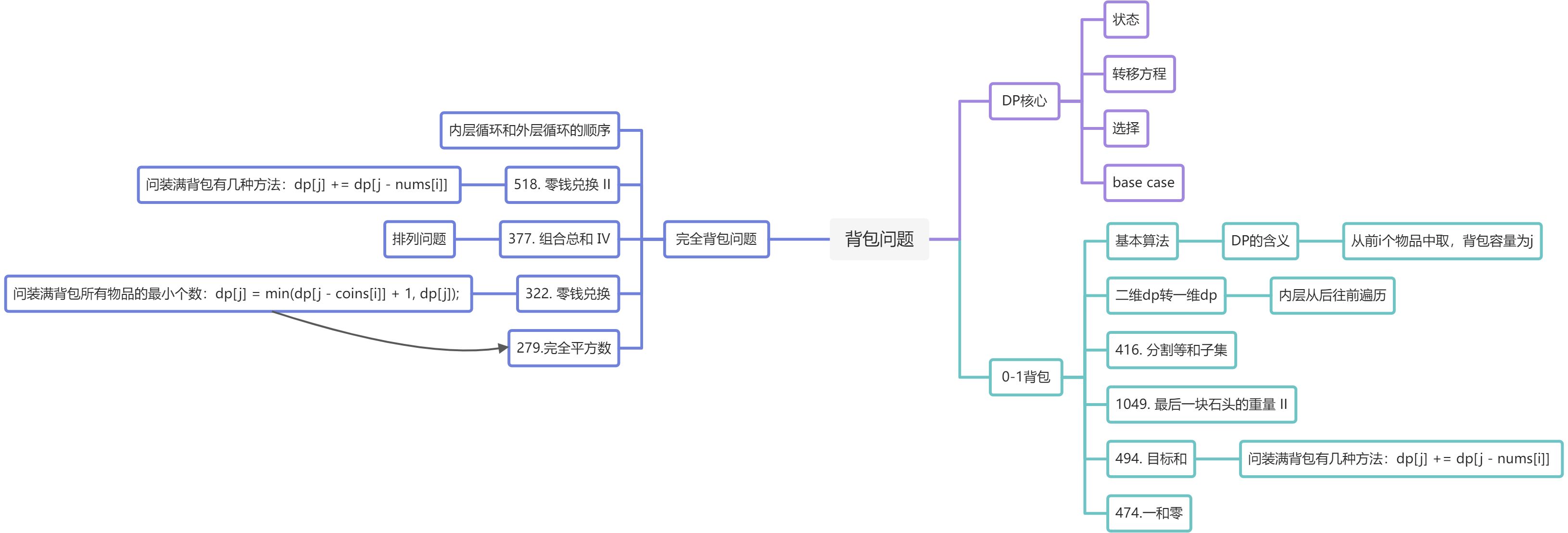
背包理论
0-1背包
:::info 有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。 ::: 使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。 :::tips 递推公式：

不放物品i：由dp[i - 1][j]推出，即背包容量为j，里面不放物品i的最大价值，此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时，物品i无法放进背包中，所以被背包内的价值依然和前面相同。)
放物品i：由dp[i - 1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值，那么dp[i - 1][j - weight[i]] + value[i]（物品i的价值），就是背包放物品i得到的最大价值

所以递归公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); :::

遍历方向问题

外层循环遍历物品；内层循环遍历容量
外层遍历容量，内层遍历物品； :::info dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向（包括正上方向）， ::: :::warning 虽然两个for循环遍历的次序不同，但是dp[i][j]所需要的数据就是左上角，根本不影响dp[i][j]公式的推导！ ::: 但先遍历物品再遍历背包这个顺序更好理解。
其实背包问题里，两个for循环的先后循序是非常有讲究的，理解遍历顺序其实比理解推导公式难多了。

二维DP table转一维DP table
在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); :::info 其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]); ::: 与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。
这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。
```
for(int i = 0; i < weight.size(); i++) { // 遍历物品
  for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
      dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
  }
}
```
:::danger 这里大家发现和二维dp的写法中，遍历背包的顺序是不一样的！
二维dp遍历的时候，背包容量是从小到大，而一维dp遍历的时候，背包是从大到小。
倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！ :::

完全背包
:::info 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i]。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。
完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。 :::
```
// 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
  for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
      dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
  }
}
```
因为可以多次使用同一物品，所以内层遍历是顺序的；

遍历顺序的不同决定了什么
:::tips 在求装满背包有几种方案的时候，认清遍历顺序是非常关键的。
如果求组合数就是外层for循环遍历物品，内层for遍历背包。518. 零钱兑换 II
如果求排列数就是外层for遍历背包，内层for循环遍历物品。377. 组合总和 Ⅳ :::

动态规划01

基本思想

背包理论

0-1背包

遍历方向问题

二维DP table转一维DP table

完全背包

遍历顺序的不同决定了什么