剖析递归行为和递归行为的时间复杂度估算

递归在系统中如何实现

举例：递归版max

int maxIteration(int &arr[],int l,int r){
    if(l==r) return arr[l];
    int mi= l+(r-l)>>1;
    int leftMax=maxIteration(arr, l,mi);
    int rightMax=maxIteration(arr,mi,r);
    return max(leftMax,rightMax);
}
int main(){
}

:::tips why 取中点用mid=l+(r-l)>>1而非mid=(l+r)>>1？

• 当数组非常大的时候，l+r很大会发生越界 :::
  递归的依赖图
  递归的过程不过是用系统栈将整个过程压栈， :::success 递归的过程：多叉树-中序遍历 :::

  master公式

  :::info :::

• ：母问题的规模

• ：子问题的规模是否都是等量的
• ：子问题执行次数
• :除了递归，其他行为的复杂度 :::tips 子问题规模相同的问题都可以用master公式求解时间复杂度； ::: 以上述例子来看：
  

时间复杂度求解可以直接根据公式来： :::success

• 
• 
• :::

归并排序

归并排序包含有递归的思想 :::info 基本思想：把一个数组分成两块，让这两块分别都有序，最后利用一个辅助数组，将这两者合并； :::

void process(vector<int> &vec,int L,int R){
    if(L==R){
        return;
    }
    int mid=L+(R-L)>>1;
    process(vec,L,mid);
    process(vec,mid+1,R);
    merge(vec,L,mid,R);
}
void merge(vector<int> &vec, int L,int M,int R){
    vector<int> help(0,R-L+1);
    int i=0;
    int p1=L;
    int p2=M+1;
    while(p1<=M&&p2<=R){
        help[i++]=vec[p1]<vec[p2]?vec[p1++]:vec[p2++];
    }
    while(p1<=M){
        help[i++]=vec[p1++];
    }
    while(p2<=R){
        help[i++]=vec[p2++];
    }
    for(i=0;i<help.size();i++){
        vec[L+i]=help[i];
    }

:::tips master公式：

所以归并排序的复杂度：额外空间复杂度 ::: 为何能达到O(NlogN)的时间复杂度；
首先看O(N^2)的算法：浪费了大量的比较行为；大量的比较后只排出了一个有序的数；
而归并排序的比较行为并未进行浪费：部分整体有序—>整体有序；

小和问题

:::info 假如用暴力枚举，那么是O(N^2)；能否用归并？
思路：

• 求小和<=>右边有多少数比i大，就有多少个i的小和；
• 可以用归并排序
• 排序的过程不可省略：排序可以告诉一共右边组有多少比左边组大；
• 左组的数与右组的数相同时，一定要先拷贝右组的，且不产生小和； :::

  int smallSum(vector<int> &vec){
    if(vec.size()<2)    return 0;
    return process(vec,0,vec.size()-1);
  }
  int process(vector<int> &vec,int l,int r){
    if(l==r)    return 0;
        int mid=l+(r-l)>>1;
    return process(vec,l,mid)//左侧小和
        +process(vec,mid+1,r)//右侧小和
        +merge(vec,l,mid,r);//merge时产生的小和
  }
  int merge(vector<int> &vec,int l,int mid,int r){
    vector<int> help(0,r-l+1);
    int i=0;
    int p1=0;
    int p2=mid+1;
    int res=0;
    while(p1<=m&&p2<=r)
    {
        res+=vec[p1]<vec[p2]?(vec[p1]*(r-p2+1)):0;
        help[i++]=vec[p2]<=vec[p1]?vec[p2++]:vec[p1++];
    }
    while(p1<=m){
        help[i++]=vec[p1++];
    }
    while(p2<=r){
        help[i++]=vec[p2++];
    }
    for(i=0;i<help.size();i++)
        vec[l+i]=help[i];
    return res;
  }

  :::tips 分左右半边的情况可以考虑利用归并； :::

  逆序对问题

  :::info 逆序对：一个数比另一个数大，但是在其左边，即为一个逆序对 ::: 逆序对问题和小和问题实际上是相同的，只需要统计右边有多少个数比i小，就有多少个i的逆序对；

快排序

引子-荷兰国旗问题

:::info 思路:

• 设定一个小于区，起始区间右端点在数组左侧（i=-1）；
• 若[i]<=num；[i]和小于区间的下一个数交换，小于区间右扩，i++；
• 若[i]>num；i++； :::

pro： :::tips

• 小于区右边界，大于区左边界
• [i]<num，[i]和小于区下一个元素交换，小于区右扩，i++
• [i]==num，i++;
• [i]>num，[i]和大于区前一个元素交换，i不变！;

终止条件？i meet 大于区； :::

快排序1.0

每次用最后一个数num做划分的界限

• 先让该数组达到：小于等于num的在左侧，大于num的在右侧（荷兰国旗问题）
• 然后将num和大于区域的第一个数交换
• 左右分别递归

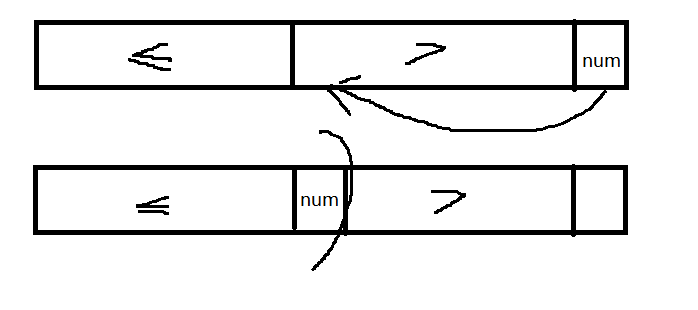
局部有序->整体有序

快排序2.0

利用荷兰国旗问题

• 用最后一个数做num
• 划分成<=>的区间
• 每次能排好一批数（=区间） :::warning 复杂度：（最差情况：划分值打的很偏） :::

快排序3.0

:::info 1.0和2.0复杂度高的原因在于划分可能会很差 :::

• 随机选一个数和最后一个数交换，用该数来做划分
• 因为随机性，可能会很好，可能会很差，但是随机性保证了平均性能；

复杂度
快排序的额外空间复杂度是log(N)级别-0

void quickSort(vector<int> &vec,int L,int R){
    if(L<R){
        swap(vec,L+rand(R-L+1),R);
        vector<int> p=partition(vec,L,R);
        quickSort(vec,L,p[0]);
        quickSort(vec,p[1]+1,R);
    }
}
vector<int> partition(vector<int> &vec,int L,int R){
    int less=L-1;//less than region
    int more=R;
    while(L<more){
        if(vec[L]<vec[R]){
            swap(vec,++less,L++);
        }else if(vec[L]==vec[R]){
            L++;
        }else{
            swap(vec,--more,L);
        }
    }
    swap(vec,R,more);
    vector<int> p={less+1,more};
    return p;
}