二叉树节点结构

  1. class Node<V>{
  2.     V value;
  3.     Node* left;
  4.     Node* right;
  5. }

:::info 遍历方式：

  • 递归遍历
  • 非递归遍历

遍历的顺序：

  • 先序
  • 中序
  • 后序 ::: 二叉树实际上是一种特殊的没有环的链表

遍历方式-递归

递归序

  1. void f(Node* head){
  2.     //1 第一次访问
  3.     if(head==nullptr)
  4.         return ;
  5.     //1
  6.     f(head->left);
  7.     //2 第二次访问
  8.     //2
  9.     f(head->right);
  10.     //3 第三次访问
  11.        //3
  12. }

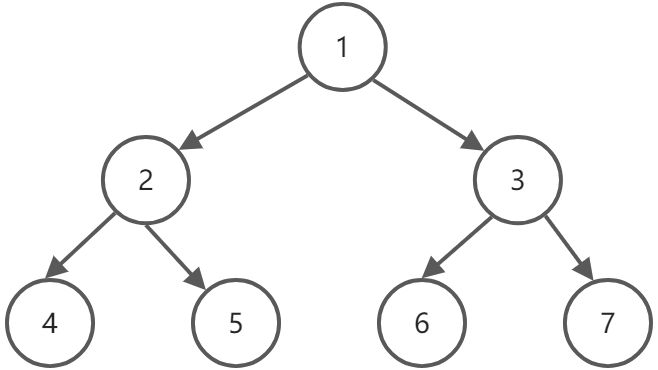
🍟05_二叉树 - 图1
按递归序遍历：1,2,4,4,4,2,5,5,5,2,1,3,6,6,6,3,7,7,7,3,1 :::tips 遍历时，可以回到自己三次！在这期间可以干点什么，也可以不干； ::: :::info 在递归序的基础上，可以提出

  • 先序
  • 中序
  • 后序 :::

    先序遍历

    :::tips 先序遍历：对于所有子树，都是先处理（打印）头节点，在处理左子树的节点，在处理右子树 ::: 1，2，4，5，3，6，7 :::tips 递归序中第一次到达该节点时打印（操作），剩下到达该节点时什么也不做，此时即为先序遍历 :::
    1. void preOrder(Node* head){
    2. if(head==nullptr)
    3.   return;
    4.      cout<<head->value;
    5.   preOrder(head->left);
    6.   preOrder(head->right);
    7. }

    中序遍历

    :::info 对于任意一个子树，先打印左子树，在打印头节点，在打印右子树 ::: 4，2，5，1，6，3，7 :::tips 递归序中第二次来到该节点时才打印，剩下什么也不做 ::: ```cpp void inOrder(Node* head){ if(head==nullptr){
    1.   return
    } inOrder(head->left); cout<value; inOrder(head->right);

}

  1. <a name="xCWCd"></a>
  2. ## 后序遍历
  3. :::info
  4. 对于任意一个子树，先打印左子树，在打印右子树，在打印头
  5. :::
  6. :::tips
  7. 在递归序中第三次来到该节点才打印，第一次第二次不处理
  8. :::
  9. ```cpp
  10. void posOrder(Node* head){
  11.     if(head==nullptr)
  12.         return;
  13.     posOrder(head->left);
  14.     posOrder(head->right);
  15.     cout<<head->value;
  16. }

非递归遍历

先序遍历

:::info 任何递归函数都可以改成非递归函数！
都是系统帮助压栈 ::: 需要准备一个栈
先序遍历：
1，2，4，5，3，6，7
🍟05_二叉树 - 图2 :::tips

  • 每次在栈中弹出一个节点，记作cur
  • 打印or处理cur
  • 先把cur的右子节点压栈，再把cur左子节点压入如果有的话

  • repeat :::

    1. void preOrder(Node* head){
    2.   if(head!=nullptr){
    3.       stack<Node> s;
    4.       Node cur;
    5.       s.push(*head);
    6.       while(!s.empty()){
    7.           cur=s.pop();
    8.           cout<<cur.value<<endl;
    9.           if(cur.right!=nullptr){
    10.               s.push(*(cur.right));
    11.           }
    12.           if(cur.left!=nullptr){
    13.               s.push(*(cur.left));
    14.           }
    15.       }
    16.   }
    17. }

    若是先序遍历想要按照头右左的顺序遍历呢？

  • 先压左子节点再压右子节点—后序

    后序遍历

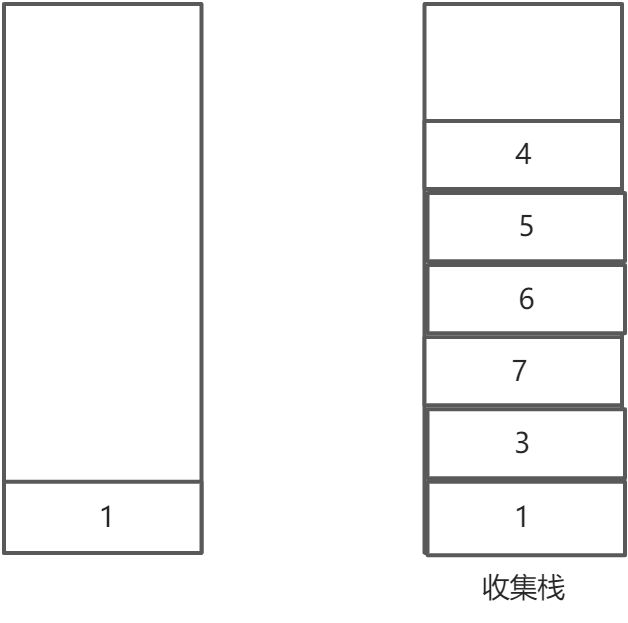    🍟05_二叉树 - 图3 :::info

  • 先弹出cur，放入收集栈

  • 对于cur的子节点，先压左再压右（头右左的递归遍历顺序）
  • repeat

  • 这样将收集栈逆序弹出，顺序就是左右头的递归顺序，因此是后续遍历 :::

    1. void posOrder(Node* head){
    2.   if(head!=nullptr){
    3.       stack<Node> s1;
    4.       stack<Node> s2
    5.       Node cur;
    6.       s.push(*head);
    7.       while(!s1.empty()){
    8.           cur=s1.pop();
    9.           s2.push(cur);
    10.           if(cur.left!=nullptr){
    11.               s.push(*(cur.left));
    12.           }
    13.           if(cur.right!=nullptr){
    14.               s.push(*(cur.right));
    15.           }
    16.       }
    17.       while(!s2.empty()){
    18.           cout<<(s2.pop()).value<<endl;
    19.       }
    20.   }
    21. }

    中序遍历

    :::info 中序遍历：左-头-右

  • 先将子树的左边界压入栈中

  • 依次弹出，弹出时打印or操作，并将弹出节点的右子树做相同的操作（左边界压栈）

  • repeat :::

    1. void preOrder(Node* head){
    2.   if(head!=nullptr){
    3.       stack<Node*> s;
    4.       while(!s.empty()||head!=nullptr){
    5.           if(head!=nullptr){
    6.               s.push(head);\\压栈在单边
    7.               head=head->left;
    8.           }else{
    9.               head=s.pop();
    10.               cout<<head->value;
    11.               head=head->right;\\不用在这里把right压栈
    12.           }
    14.        }
    15.   }
    16. }

    :::info 所有的数都是可以被左边界分解的

  • 左边界放到栈里：头—>左的顺序，那么弹出的顺序必然是左—>头；

  • 弹出时对右边界做同样的操作。意味着对于右树后做先左再头的打印；

  • 相当于把整棵树都按左边界分解了，但是右树后做！ :::

    二叉树的宽度优先遍历

    :::info 二叉树的先序遍历就是其深度优先遍历

  • 宽度优先遍历？

  • 队列：先进先出 :::

  • 先把头节点放入队列中

  • 弹出节点并打印
  • 先放入弹出节点的左子节点，再放入右子节点

  • repeat

    1. void BFS(Node* head) {
    2.   if (head == nullptr) {
    3.       return;
    4.   }
    5.   queue<Node*> q;
    6.   q.push(head);
    7.   while (!q.empty()) {
    8.       Node* cur = q.front();
    9.       q.pop();
    10.       cout << cur->_value << endl;
    11.       if (cur->_left != nullptr) {
    12.           q.push(cur->_left);
    13.       }
    14.       if (cur->_right != nullptr) {
    15.           q.push(cur->_right);
    16.       }
    17.   }
    18. }

    Example

    :::info 求一个二叉树的最大宽度？

  • 知道每个节点所在那一层？

  • 统计每一层的节点个数 :::

    1. void BFS_n(Node* head) {//代码有问题，C++中unordered_map未匹配
    2.   if (head == nullptr) {
    3.       return;
    4.   }
    5.   queue<Node*> q;
    6.   q.push(head);
    7.   int currentLevelNodes=0;
    8.   int curLevel=1;
    9.   int maxNum=-1;
    10.   unordered_map<Node*,int> levelMap;
    11.   levelMap.insert(head,1);
    12.   while (!q.empty()) {
    13.       Node* cur = q.front();
    14.       int curNodelevel=levelMap.find(cur);
    16.       if(curNodeLevel==curLevel){
    17.           currentLevelNodes++;
    18.       }else{
    19.           maxNum=max(currentLevelNodes,max);
    20.           curLevel++;
    21.           currentLevelNodes=1;
    22.       }
    23.       q.pop();
    24.       if (cur->_left != nullptr) {
    25.           levelMap.insert(cur->left,curLevel+1);
    26.           q.push(cur->_left);
    27.       }
    28.       if (cur->_right != nullptr) {
    29.           levelMap.insert(cur->right,curLevel+1)
    30.           q.push(cur->_right);
    31.       }
    32.   }
    33. }