算法进阶

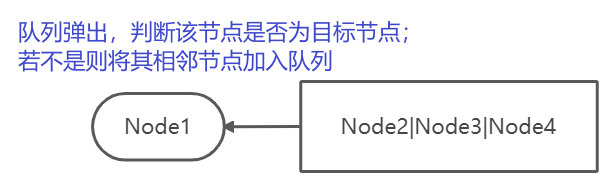
单调栈

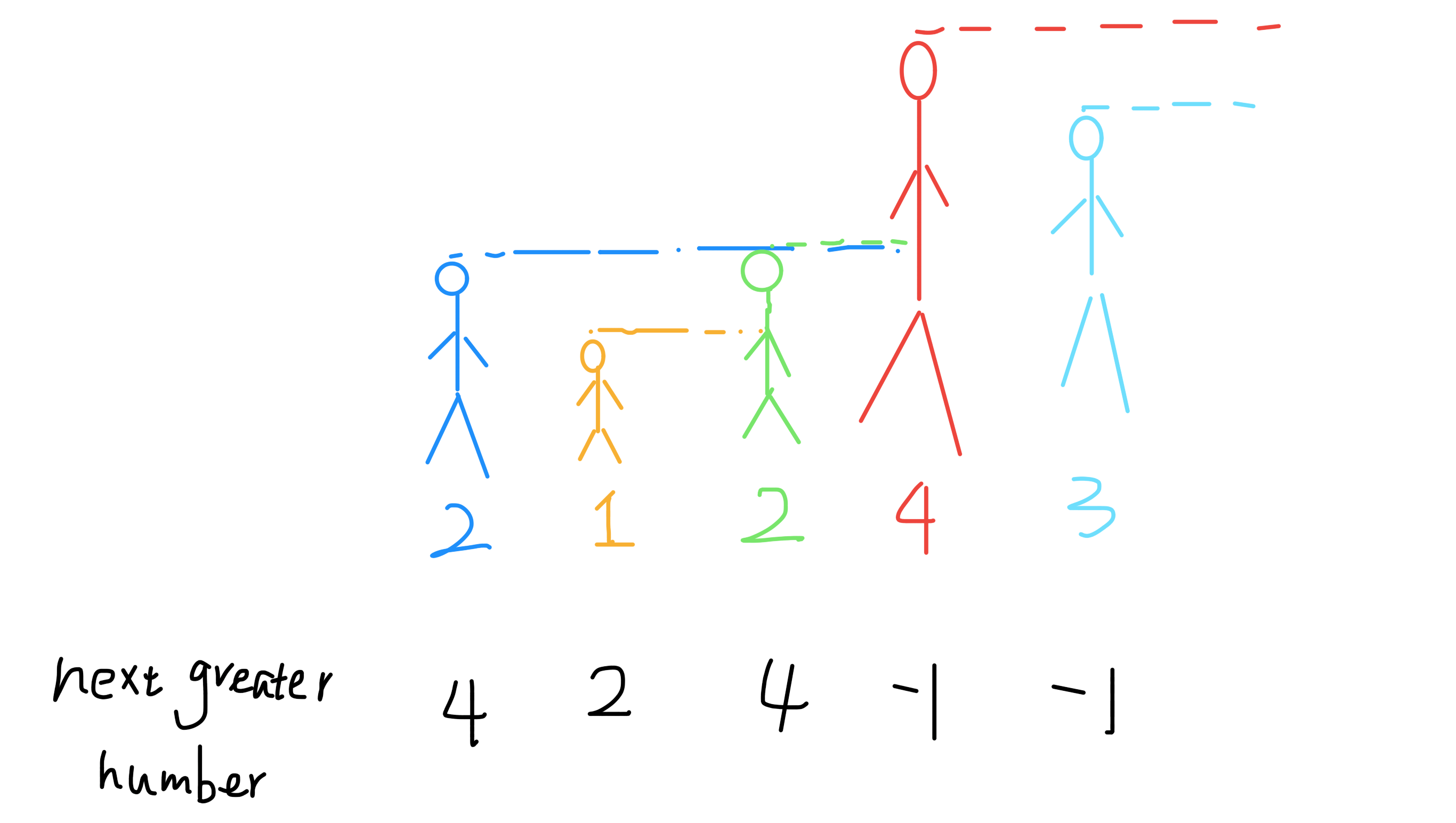
function MonotoStack(arr) {
  // 单调栈
  let result = [],
    stack = [];
  for (let i = arr.length - 1; i >= 0; i--) {
    while (stack.length != 0 && stack[stack.length - 1] <= arr[i]) {
      stack.pop();
    }
    result[i] = stack.length == 0 ? -1 : stack[stack.length - 1];
    stack.push(arr[i]);
  }
  return result;
}

单调队列

API

class MonotonicQueue {
    // 在队尾添加元素 n
    void push(int n);
    // 返回当前队列中的最大值
    int max();
    // 队头元素如果是 n，删除它
    void pop(int n);
}

「单调队列」的核心思路和「单调栈」类似。单调队列的 push 方法依然在队尾添加元素，但是要把前面比新元素小的元素都删掉：

BFS算法（广度优先搜索）

在图的数据结构中称作广度优先搜索，在树的数据结构中则体现为层次遍历；两者的区别在于树的自顶向下的结构决定了遍历时不需要判断节点是否被访问过。
常见的场景：问题的本质就是在一副【图】中找到从起点到终点的最小距离。如走迷宫、连连看游戏拐点不得多于两个等等。

遍历框架

// 计算从起点 start 到终点 target 的最近距离
int BFS(Node start, Node target) {
    Queue<Node> queue; // 核心数据结构
    Set<Node> visited; // 避免走回头路
    queue.push(start); // 将起点加入队列
    visited.add(start);
    int step = 0; // 记录扩散的步数
    while (queue not empty) {
        int sz = queue.size();
        /* 将当前队列中的所有节点向四周扩散 */
        for (int i = 0; i < sz; i++) { // 每次都应该对此时的队列做一次“清除”, sz当前是固定的
            Node cur = queue.shift(); // 拿出对头
            /* 划重点：这里判断是否到达终点 */
            if (cur is target)
                return step;
            /* 将 cur 的相邻节点加入队列 */
            for (Node x : cur.adj())
                if (x not in visited) {
                    queue.push(x);
                    visited.add(x);
                }
        }
        /* 划重点：更新步数在这里 */
        step++;
    }
}

示意图

例题

二叉树的最小高度

var minDepth = function (root) {
    if (root == null) return 0;
    let queue = [root], height = 1;
    while (queue.length !== 0) {
        let len = queue.length;
        while (len--) {
            let node = queue.shift();
            if (node.left === null && node.right === null) return height;
            if (node.left !== null) queue.push(node.left);
            if (node.right !== null) queue.push(node.right);
        }
        height += 1;
    }
};

也可以使用深度优先搜索（DFS），但是时间复杂度相对更高。可以这样想象一下：DFS 是线，BFS 是面；DFS 是单打独斗，BFS 是集体行动。

DFS算法（深度优先搜索）

在图的数据结构中称作深度优先搜索

回溯算法

双指针技巧

再分为两类，一类是「快慢指针」，一类是「左右指针」。前者解决主要解决链表中的问题，比如典型的判定链表中是否包含环；后者主要解决数组（或者字符串）中的问题，比如二分查找。

一、快慢指针的常见算法

快慢指针一般都初始化指向链表的头结点 head，前进时快指针 fast 在前，慢指针 slow 在后，巧妙解决一些链表中的问题。
1、判定链表中是否含有环
2、已知链表中含有环，返回这个环的起始位置
3、寻找链表的中点
4、寻找链表的倒数第 k 个元素

二、左右指针的常用算法

左右指针在数组中实际是指两个索引值，一般初始化为 left = 0, right = nums.length - 1 。
1、二分查找
前文「二分查找」有详细讲解，这里只写最简单的二分算法，旨在突出它的双指针特性。
2、两数之和

3、反转数组
4、滑动窗口算法
一、最小覆盖子串 - LeeCode 76
二、找到字符串中所有字母异位词 - LeeCode 438
三、无重复字符的最长子串 - LeeCode 3
最后总结：
通过上面三道题，我们可以总结出滑动窗口算法的抽象思想：

int left = 0, right = 0;
while (right < s.size()) {
    window.add(s[right]);
    right++;
    while (valid) {
        window.remove(s[left]);
        left++;
    }
}

其中 window 的数据类型可以视具体情况而定，比如上述题目都使用哈希表充当计数器，当然你也可以用一个数组实现同样效果，因为我们只处理英文字母。
稍微麻烦的地方就是这个 valid 条件，为了实现这个条件的实时更新，我们可能会写很多代码。比如前两道题，看起来解法篇幅那么长，实际上思想还是很简单，只是大多数代码都在处理这个问题而已。

滑动窗口

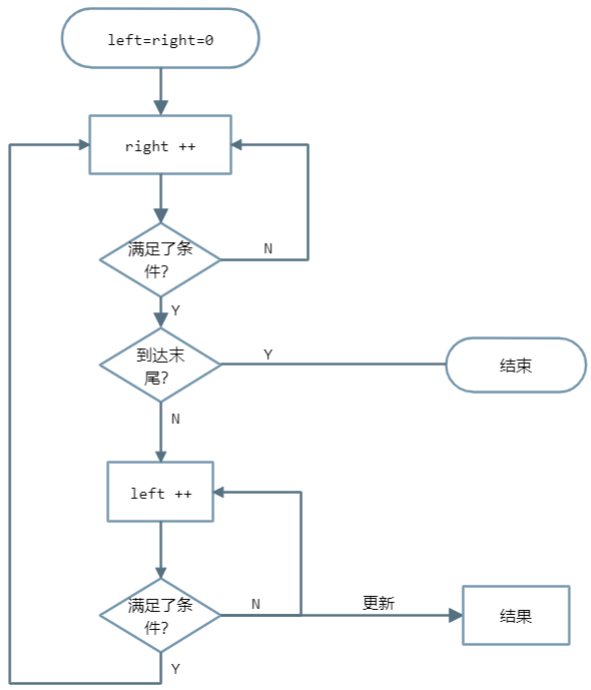
代码如下：

function slideWindow(s = "", t = "") {
    let window = {}; // window就是我们所需的窗口了，也可用Map
    let need = new Map(); // need是我们需要凑齐的字符
    for (let i of t) {
        if (need.has(i)) need.set(i, need.get(i) + 1);
        else need.set(i, 1);
    } // Map { 'b' => 2 }
    let left = 0, // 滑动窗口的左下标
        right = 0, // 右下标
        valid = 0, // valid变量表示窗口中满足need条件的字符个数
        start = 0, // 最终结果的左下标
        len = Infinity, // 最终与左下标的偏移量，即最终结果的长度
        INT_MAX = Infinity;
    while (right < s.length) {
        let c = s[right];
        right++;
        // 字符进入滑动窗口
        if (window[c]) window[c] += 1;
        else window[c] = 1;
        // 判断匹配个数
        if (window[c] == need.get(c)) valid++;
        // 匹配个数满足则更新len，并从左边缩小窗口
        while (valid == need.size) {
            if (right - left < len) {
                len = right - left;
                start = left;
            }
            let d = s[left];
            left++;
            if (need.get(d)) {
                if (need.get(d) === window[d]) {
                    valid -= 1;
                }
                window[d] -= 1;
            }
        }
    }
    return len == INT_MAX ? "" : s.slice(start, start + len);
}

LRU算法

参考资料：labuladong - LRU详解

介绍

LRU算法是一种“缓存淘汰策略”，在《操作系统》的内存管理中有介绍。全称是“Least Recently Used”，意思是“最近最少使用”，那就意味着淘汰“最少使用的数据”。
算法思想：设想一个队列，队头是很少使用的数据，而队尾是新的数据。当读取某个数据时，就更新该数据的位置，将数据位置提升至队尾；当存放数据时，从队尾存放，若缓存中存在该数据，则删除旧数据，再从队尾插入；若缓存满了，则需要先删除对头的数据，再将新数据放在队尾。

数据结构

接收capacity参数作为缓存最大容量；两个API：put(key, val)用于放入数据，get(key)用于读取数据。
要求两个API都是O(1)的时间复杂度。

如何实现

• put(key, val)的操作是尾部插入数据，而且可能涉及到头部删除数据，插入删除时间为O(1)，使用链表的数据结构可以实现；
• get(key)操作是读取对应数据，涉及到先删除数据再在尾部插入数据，链表还是顺序表都需要O(n)时间进行查找，而使用哈希表可以达到O(1)的时间要求。

要同时满足以上两种条件，就可以结合两种数据结构，形成一种新的数据结构：哈希链表（LinkedHashMap）。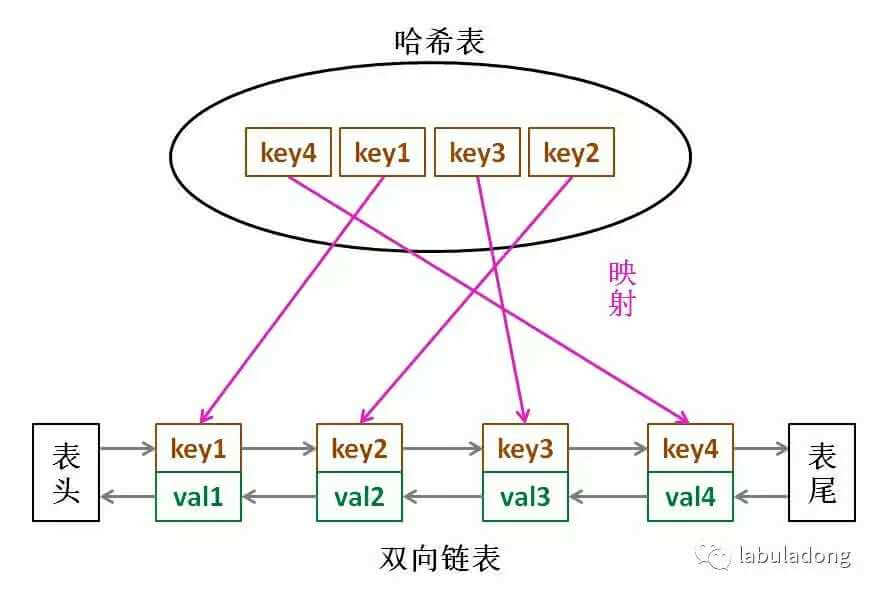

Q1：为什么是双向链表，而不能是单向链表：
A1：因为get操作的时候，需要先删除对应数据的结点，再尾部插入。删除操作需要知道前序结点指针，单链表只能知道后序结点，不知道前序结点，而双向链表可以。
Q2：哈希表中存储了key，链表中可不可以只存储val：
A2：

代码实现

思路：

1. 构建结点的数据结构
2. 构建双向链表的数据结构及API
3. 将双向链表和哈希表进行结合

结点的数据结构：

class Node {
  // 双向链表的结点的数据结构
  constructor(key, val) {
    this.key = key;
    this.val = val;
    this.next = null;
    this.prev = null;
  }
}

构建符合的双向链表的数据结构：

class DoubleList {
  constructor() {
    // 这里头指针和尾指针都分别创建了"虚"结点，方便api实现
    // 否则删除操作需要判断是否删除的是头结点、中间结点、尾结点
    this.head = new Node(0, 0);
    this.tail = new Node(0, 0);
    this.head.next = this.tail;
    this.tail.prev = this.head;
    this.size = 0;
  }
  addLast(nodex) {
    // 链表尾部添加节点，时间O(1)
    nodex.prev = this.tail.prev;
    nodex.next = this.tail;
    nodex.prev.next = nodex;
    this.tail.prev = nodex;
    this.size += 1;
  }
  remove(nodex) {
    nodex.prev.next = nodex.next;
    nodex.next.prev = nodex.prev;
    this.size -= 1;
  }
  removeFirst() {
    if (this.head.next == this.tail) return null;
    let needDeleteNode = this.head.next;
    this.remove(needDeleteNode);
    return needDeleteNode;
  }
  sizeLink() {
    return this.size;
  }
}

将双向链表和哈希表结合：
先不慌去实现 LRU 算法的 get 和 put 方法。由于我们要同时维护一个双链表 cache 和一个哈希表 map，很容易漏掉一些操作，比如说删除某个 key 时，在 cache 中删除了对应的 Node，但是却忘记在 map 中删除 key。
解决这种问题的有效方法是：在这两种数据结构之上提供一层抽象 API。就是尽量让 LRU 的主方法 get 和 put 避免直接操作 map 和 cache 的细节。

class LRUCache {
  constructor(capacity) {
    this.map = new Map(); // 哈希表
    this.cache = new DoubleList(); // 双向链表
    this.cap = capacity; // 容量
  }
  // 将某个key提升为最近使用的，操作链表
  makeRecently(key) {
    // 哈希表中先查找
    let nodex = this.map.get(key);
    // 链表中先删除再尾部添加
    this.cache.remove(nodex);
    this.cache.addLast(nodex);
  }
  // 添加最近使用的元素
  addRecently(key, val) {
    let nodex = new Node(key, val);
    // 链表尾部添加
    this.cache.addLast(nodex);
    // 哈希表中添加
    this.map.set(key, nodex);
  }
  // 删除某一个key
  deleteKey(key) {
    let nodex = this.map.get(key);
    this.cache.remove(nodex);
    this.map.delete(key);
  }
  // 删除最久未使用的元素
  removeLeastRecently() {
    let deleteNode = this.cache.removeFirst();
    this.map.delete(deleteNode.key);
  }
  // get 方法
  get(key) {
    if (!this.map.has(key)) {
      return -1;
    }
    this.makeRecently(key);
    return this.map.get(key).val;
  }
  // put方法
  put(key, val) {
    if (this.map.has(key)) {
      // 删除旧的数据
      this.deleteKey(key);
      // 新插入数据为最近使用的数据
      this.addRecently(key.val);
      return;
    }
    if (this.cap == this.cache.sizeLink()) {
      // 缓存满了，先删除最近未使用的数据
      this.removeLeastRecently();
    }
    // 新插入数据为最近使用的数据
    this.addRecently(key, val);
  }
}

优先队列

特点：插入、删除时，元素会自动排序。根据每次优先删除队列中最小还是最大的元素，分别称作“最小优先队列”和“最大优先队列”。优先队列其实就是基于二叉堆这个数据结构。
最大优先队列API：插入一个元素、删除最大的元素并返回。插入元素涉及到“上浮”操作，删除最大元素的步骤是：先将堆顶元素与最后一个元素替换，然后删除最后元素，并将堆顶元素进行“下沉”操作。
堆的表示：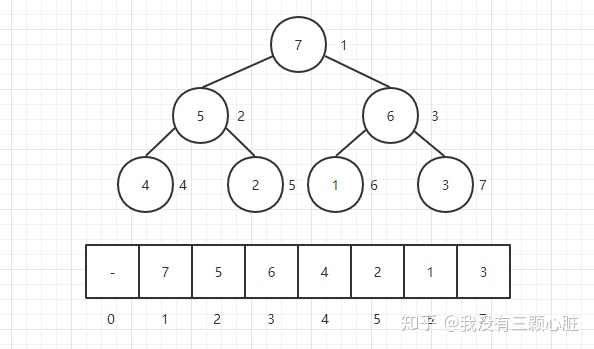

下标关系：left_child = parent 2；right_child = parent 2+1；parent = child / 2；
数据结构：