Sites：

  1. https://www.bigocheatsheet.com/，一个备忘清单，列了各个算法的复杂度

10大排序算法

参考：

  1. 十大经典排序算法
  2. 排序算法动画

基本描述

算法基础 - 图1

排序算法比较

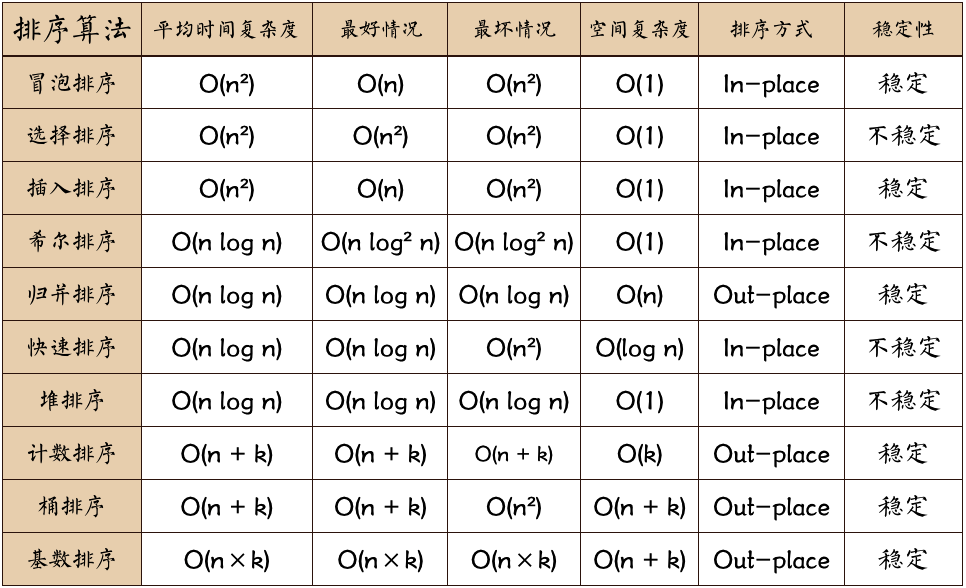
算法基础 - 图2
稳定性：如果原先a在b前面，排序后a仍然在b前面，它们的相对性不变，则具有稳定性。

冒泡

  1. function bubbleSort(arr) {
  2.     length = arr.length
  3.     for (let i = 0; i < length; i++) {
  4.         for (let j = i + 1; j < length; j++) {
  5.             if (arr[i] > arr[j]) {
  6.                 let temp = arr[i]
  7.                 arr[i] = arr[j]
  8.                 arr[j] = temp
  9.             }
  10.         }
  11.     }
  12. }

冒泡改进（错误的）

冒泡改进：设置一个flag来表示若未发生交换则表示排序结束

  1. function bubbleSort(arr) {
  2.     length = arr.length
  3.     for (let i = 0; i < length; i++) {
  4.         let flag = true
  5.         for (let j = i + 1; j < length; j++) {
  6.             if (arr[i] > arr[j]) {
  7.                 flag = false
  8.                 let temp = arr[i]
  9.                 arr[i] = arr[j]
  10.                 arr[j] = temp
  11.             }
  12.         }
  13.         if (flag) {
  14.             break
  15.         }
  16.     }
  17.     return arr
  18. }

快速排序

  1. function quickSort(arr) {
  2.     // 手写快速排序
  3.     function mySort(arr, begin, end) {
  4.         let pivot;
  5.         if (begin < end) {
  6.             pivot = helper(arr, begin, end) // 这里arr传入之后，就会对arr进行处理改变
  7.             mySort(arr, begin, pivot - 1)
  8.             mySort(arr, pivot + 1, end)
  9.         }
  10.     }
  12.     function helper(arr, begin, end) { // 将arr以baseValue为中心进行分类
  13.         let baseValue = arr[begin];
  14.         while (begin < end) {
  15.           // 从后面开始查找，直到找到一个小于基准的值就停止，并交换
  16.             while (begin < end && arr[end] >= baseValue) { 
  17.                 end -= 1
  18.             }
  19.             [arr[begin], arr[end]] = [arr[end], arr[begin]]
  20.           // 从前面开始查找，直到找到一个大于基准的值就停止，并交换
  21.             while (begin < end && arr[begin] <= baseValue) {
  22.                 begin += 1
  23.             }
  24.             [arr[begin], arr[end]] = [arr[end], arr[begin]]
  25.         }
  26.         return begin
  27.     }
  28.     mySort(arr, 0, arr.length - 1)
  29.     return arr
  30. }

归并排序

  1. //归并排序
  2. function mergeSort(arr) {
  3.     if (arr.length <= 1) return arr // 数组长度小于1则直接返回
  4.     const midIndex = arr.length / 2 | 0 // 中间索引
  5.     const leftArr = arr.slice(0, midIndex) // 左边的数组
  6.     const rightArr = arr.slice(midIndex, arr.length) // 右边的数组
  7.     return merge(mergeSort(leftArr), mergeSort(rightArr))
  8. }
  10. function merge(leftArr, rightArr) { // 合并两个有序数组
  11.     const result = []
  12.     while (leftArr.length && rightArr.length) {
  13.         leftArr[0] <= rightArr[0] ? result.push(leftArr.shift()) : result.push(rightArr.shift())
  14.     }
  15.     while (leftArr.length) result.push(leftArr.shift())
  16.     while (rightArr.length) result.push(rightArr.shift())
  17.     return result
  18. }
  20. //我的写法
  21. function mergeSortedTwoArr(leftArr = [], rightArr = []) {
  22.   let i = 0,
  23.     j = 0,
  24.     result = [];
  25.   while (i < leftArr.length) {
  26.     while (j < rightArr.length) {
  27.       if (leftArr[i] < rightArr[j]) {
  28.         result.push(leftArr[i++]);
  29.         break;
  30.       } else {
  31.         result.push(rightArr[j++]);
  32.         break;
  33.       }
  34.     }
  35.     if (j === rightArr.length) break;
  36.   }
  37.     if (i === leftArr.length) result = result.concat(rightArr.slice(j));
  38.     if (j === rightArr.length) result = result.concat(leftArr.slice(i));
  39.   return result;
  40. }

选择排序

插入排序

希尔排序

堆排序

计数排序

桶排序

基数排序

7大查找算法

查找算法分类：
1）按静态查找、动态查找分类：查找表中是否有删除和插入操作。
2）按有序查找、无序查找分类：查找表是否有序。
平均查找长度（ASL）：

顺序查找

适用场景：适合于存储结构为顺序存储或链式存储的线性表。

二分查找

使用条件：已排序的列表；若无序列表则先进行排序再使用。适用于静态查找表，如果有插入删除的操作来维护有序的排序则不太适用。
时间复杂度：平均和最坏情况都是o(logn)；
空间复杂度：o(1)；
记忆细节：看初始right是否是数组最后一个数，若是则while那里为”<=”，后面的mid修改也要有”+1”、”-1”的操作。

  1. function BinarySearch(arr, target) {
  2.   // 明确三个数left, right, mid
  3.   let left = 0;
  4.   let right = arr.length - 1; // 注意点1
  5.   let mid;
  6.   while (left <= right) { // 注意点2
  7.     mid = parseInt(left + (right - left) / 2);
  8.     if (target === arr[mid]) return mid;
  9.     else if (target < arr[mid]) right = mid - 1; // 点3
  10.     else if (arr[mid] < target) left = mid + 1; // 点4
  11.   }
  12.   return -1;
  13. }

插值查找（二分优化）

在二分查找中，由于mid = (low+high) / 2，因此每次比较的都是中间值。
我们来思考这样一个场景：使用字典查找单词时，比如查找“zero”这个单词，我们习惯上直接翻到字典后面的页数去慢慢找，而不是字典页数对半查找。因此就有了插值查找的概念。插值查找就是二分查找的优化。
插值查找的mid = low + (target - arr[low])/(arr[high] - arr[low])*(high - low)，这样处理以后的mid相比于二分查找的mid会更靠近查找目标的下标。
时间复杂度：平均时间复杂度相对于二分查找有改进，为o(log(logn))，最坏的为o(logn)。

  1. // 相比于二分查找，只需要修改mid
  2. mid = parseInt(
  3.       left + ((target - arr[left]) / (arr[right] - arr[left])) * (right - left)
  4.     );

斐波那契查找（二分优化）


算法基础 - 图3

树表查找

二叉树查找算法：二叉搜索树（BST）

定义：递归地对于每个根节点来说，若其左子树存在则左子树的所有节点值小于根节点；若其右子树存在则右子树的所有节点值大于根节点。
平均时间复杂度：平均时间复杂度o(logn)；最坏时间复杂度：o(n)，发生在二叉树极度不平衡的情况下，比如树中绝大多数都是单子树，是的需要进行n次查找。为了改进这样的问题，设计出了平衡二叉树。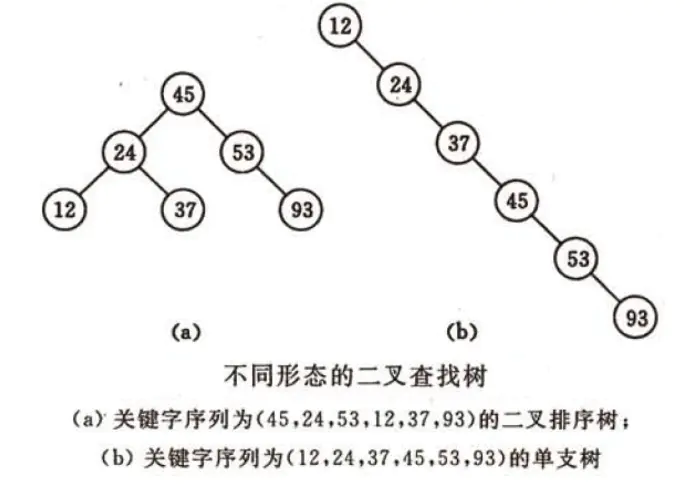
算法基础 - 图4

平衡查找树：平衡二叉树

定义：递归地对于每个根节点来说，若根节点存在，则其左右子树的高度相差不大于1。
有难度的是将不平衡的二叉查找树转化为平衡二叉查找树。
时间复杂度：插入、查找都为o(logn)。

平衡查找树：2-3查找树

定义：2-3指的是根节点的孩子可以是2个也可以是3个，所以不是二叉树。

分块查找

是顺序查找的一种改进方法。块与块之间必须有序，但块内可以无序。先通过顺序查找或二分查找找到属于哪个块，然后再块内查找。

哈希查找

哈希表也叫做散列表，原理是可以根据给定的键(key)直接访问内存存储位置的数据，那根据给定的键直接访问到数据的这个过程，或者说这种映射关系是由散列函数来完成的。所以我们在拿到一组数据的时候，数组中每个项通过散列函数进行映射，映射关系需要额外的存储空间，所以哈希表是很典型的以空间换时间的算法。下次当我们要查找某个数时，只要通过散列函数就能拿到映射在内存中的数据。
实现散列函数有几种方法：

  1. 直接定址法：f(x) = a*x + b类似这样的；
  2. 随机数法；
  3. 余数法：f(x) = x mod p；
  4. ……

但都有相同的愿望，都是想通过某种转换关系，让关键字(key)尽可能分散到指定大小的顺序结构之中。越分散，说明之后查找时间复杂度越小，空间复杂度越高。但分散的时候可能将多个项映射到同一个“槽”之中，这种情况就称作“哈希冲突”，所以我们需要一种办法来解决这种情况，解决的过程叫做“冲突解决”。常见的有2种解决冲突的办法：拉链法、线性探测法。
查找平均时间复杂度：o(1)。