Map 是一种很常见的数据结构,用于存储一些无序的键值对。在主流的编程语言中,默认就自带它的实现。C、C++ 中的 STL 就实现了 Map,JavaScript 中也有 Map,Java 中有 HashMap,Swift 和 Python 中有 Dictionary,Go 中有 Map,Objective-C 中有 NSDictionary、NSMutableDictionary。
上面这些 Map 都是线程安全的么?答案是否定的,并非全是线程安全的。那如何能实现一个线程安全的 Map 呢?想回答这个问题,需要先从如何实现一个 Map 说起。
一. 选用什么数据结构实现 Map ?
Map 是一个非常常用的数据结构,一个无序的 key/value 对的集合,其中 Map 所有的 key 都是不同的,然后通过给定的 key 可以在常数时间 O(1) 复杂度内查找、更新或删除对应的 value。
要想实现常数级的查找,应该用什么来实现呢?读者应该很快会想到哈希表。确实,Map 底层一般都是使用数组来实现,会借用哈希算法辅助。对于给定的 key,一般先进行 hash 操作,然后相对哈希表的长度取模,将 key 映射到指定的地方。
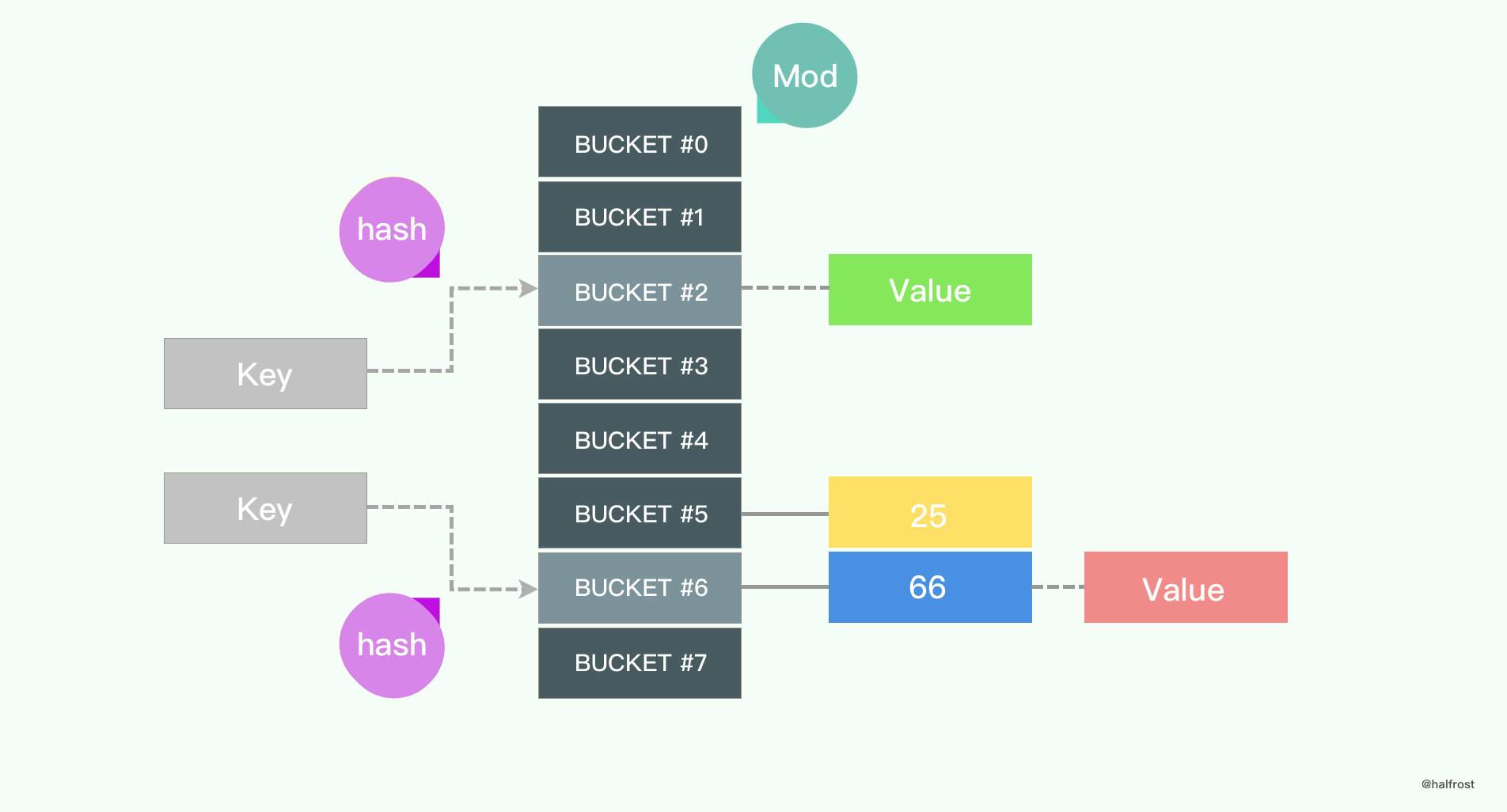
哈希算法有很多种,选哪一种更加高效呢?
1. 哈希函数
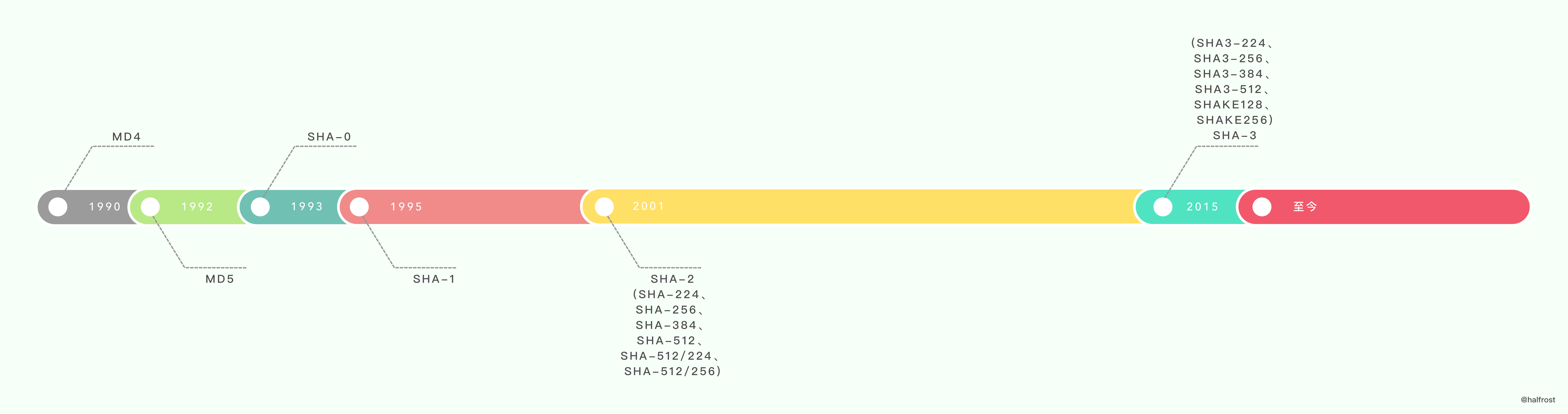
MD5 和 SHA1 可以说是目前应用最广泛的 Hash 算法,而它们都是以 MD4 为基础设计的。
MD4(RFC 1320) 是 MIT 的 Ronald L. Rivest 在 1990 年设计的,MD 是 Message Digest(消息摘要) 的缩写。它适用在 32 位字长的处理器上用高速软件实现——它是基于 32 位操作数的位操作来实现的。
MD5(RFC 1321) 是 Rivest 于 1991 年对 MD4 的改进版本。它对输入仍以 512 位分组,其输出是 4 个 32 位字的级联,与 MD4 相同。MD5 比 MD4 来得复杂,并且速度较之要慢一点,但更安全,在抗分析和抗差分方面表现更好。
SHA1 是由 NIST NSA 设计为同 DSA 一起使用的,它对长度小于 264 的输入,产生长度为 160bit 的散列值,因此抗穷举 (brute-force)
性更好。SHA-1 设计时基于和 MD4 相同原理, 并且模仿了该算法。
常用的 hash 函数有 SHA-1,SHA-256,SHA-512,MD5 。这些都是经典的 hash 算法。在现代化生产中,还会用到现代的 hash 算法。下面列举几个,进行性能对比,最后再选其中一个源码分析一下实现过程。
(1) Jenkins Hash 和 SpookyHash
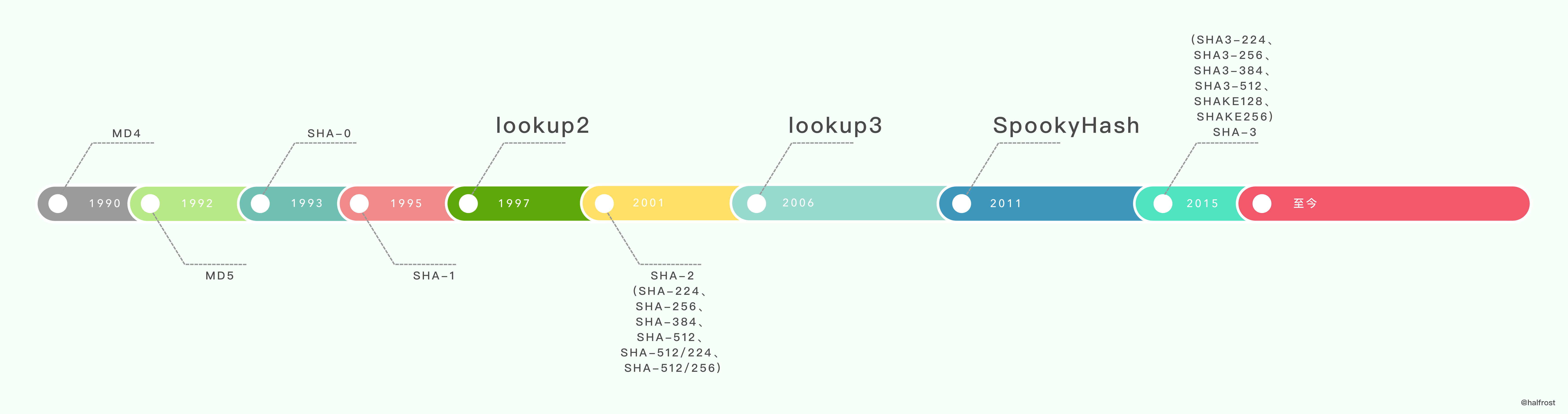
1997 年 Bob Jenkins 在《 Dr. Dobbs Journal》杂志上发表了一片关于散列函数的文章《A hash function for hash Table lookup》。这篇文章中,Bob 广泛收录了很多已有的散列函数,这其中也包括了他自己所谓的 “lookup2”。随后在 2006 年,Bob 发布了 lookup3。lookup3 即为 Jenkins Hash。更多有关 Bob’s 散列函数的内容请参阅维基百科:Jenkins hash function。memcached 的 hash 算法,支持两种算法:jenkins, murmur3,默认是 jenkins。
2011 年 Bob Jenkins 发布了他自己的一个新散列函数
SpookyHash(这样命名是因为它是在万圣节发布的)。它们都拥有 2 倍于 MurmurHash 的速度,但他们都只使用了 64 位数学函数而没有 32 位版本,SpookyHash 给出 128 位输出。
(2) MurmurHash
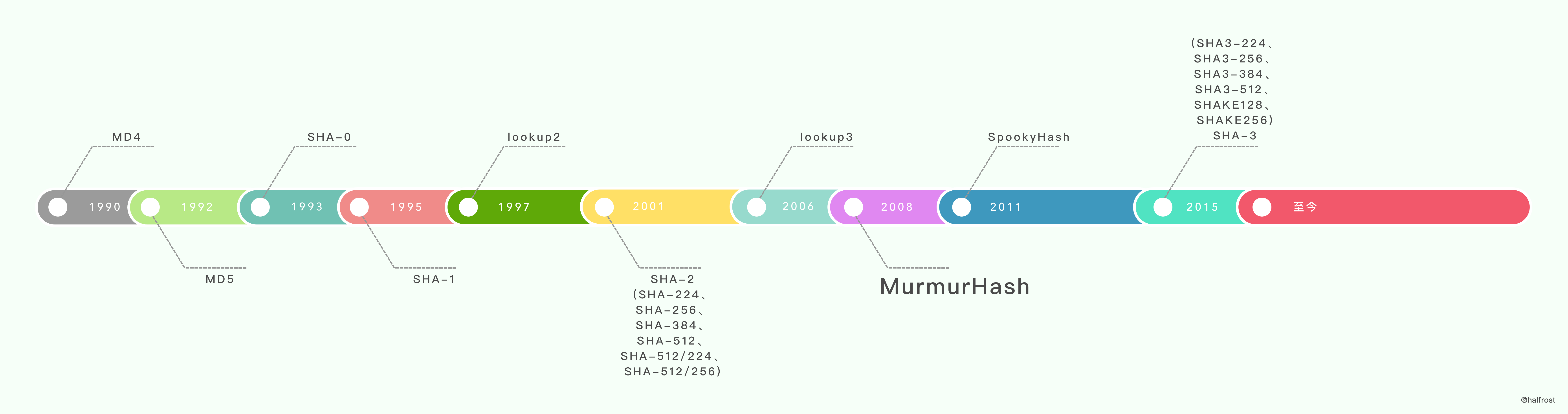
MurmurHash 是一种非加密型哈希函数,适用于一般的哈希检索操作。
Austin Appleby 在 2008 年发布了一个新的散列函数——MurmurHash。其最新版本大约是 lookup3 速度的 2 倍(大约为 1 byte/cycle),它有 32 位和 64 位两个版本。32 位版本只使用 32 位数学函数并给出一个 32 位的哈希值,而 64 位版本使用了 64 位的数学函数,并给出 64 位哈希值。根据 Austin 的分析,MurmurHash 具有优异的性能,虽然 Bob Jenkins 在《Dr. Dobbs article》杂志上声称 “我预测 MurmurHash 比起 lookup3 要弱,但是我不知道具体值,因为我还没测试过它”。MurmurHash 能够迅速走红得益于其出色的速度和统计特性。当前的版本是 MurmurHash3,Redis、Memcached、Cassandra、HBase、Lucene 都在使用它。
下面是用 C 实现 MurmurHash 的版本:
uint32_t murmur3_32(const char *key, uint32_t len, uint32_t seed) {static const uint32_t c1 = 0xcc9e2d51;static const uint32_t c2 = 0x1b873593;static const uint32_t r1 = 15;static const uint32_t r2 = 13;static const uint32_t m = 5;static const uint32_t n = 0xe6546b64;uint32_t hash = seed;const int nblocks = len / 4;const uint32_t *blocks = (const uint32_t *) key;int i;for (i = 0; i < nblocks; i++) {uint32_t k = blocks[i];k *= c1;k = (k << r1) | (k >> (32 - r1));k *= c2;hash ^= k;hash = ((hash << r2) | (hash >> (32 - r2))) * m + n;}const uint8_t *tail = (const uint8_t *) (key + nblocks * 4);uint32_t k1 = 0;switch (len & 3) {case 3:k1 ^= tail[2] << 16;case 2:k1 ^= tail[1] << 8;case 1:k1 ^= tail[0];k1 *= c1;k1 = (k1 << r1) | (k1 >> (32 - r1));k1 *= c2;hash ^= k1;}hash ^= len;hash ^= (hash >> 16);hash *= 0x85ebca6b;hash ^= (hash >> 13);hash *= 0xc2b2ae35;hash ^= (hash >> 16);return hash;}
(3) CityHash 和 FramHash
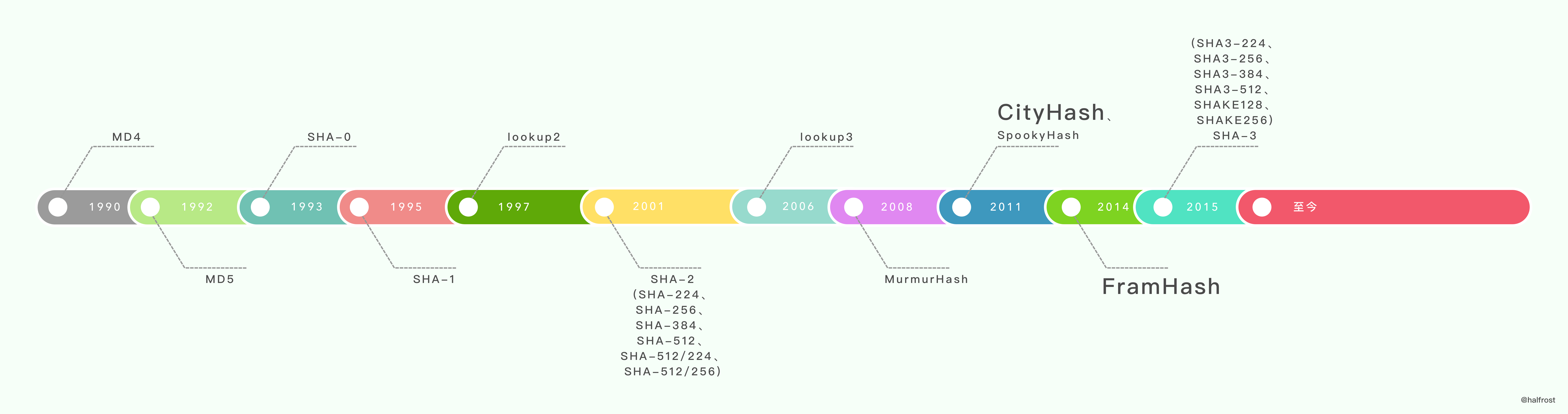
这两种算法都是 Google 发布的字符串算法。
CityHash 是 2011 年 Google 发布的字符串散列算法,和 murmurhash 一样,属于非加密型 hash 算法。CityHash 算法的开发是受到了 MurmurHash 的启发。其主要优点是大部分步骤包含了至少两步独立的数学运算。现代 CPU 通常能从这种代码获得最佳性能。CityHash 也有其缺点:代码较同类流行算法复杂。Google 希望为速度而不是为了简单而优化,因此没有照顾较短输入的特例。Google 发布的有两种算法:cityhash64 与 cityhash128。它们分别根据字串计算 64 和 128 位的散列值。这些算法不适用于加密,但适合用在散列表等处。CityHash 的速度取决于 CRC32 指令,目前为 SSE 4.2(Intel Nehalem 及以后版本)。
相比 Murmurhash 支持 32、64、128bit, Cityhash 支持 64、128、256bit 。
2014 年 Google 又发布了 FarmHash,一个新的用于字符串的哈希函数系列。FarmHash 从 CityHash 继承了许多技巧和技术,是它的后继。FarmHash 有多个目标,声称从多个方面改进了 CityHash。与 CityHash 相比,FarmHash 的另一项改进是在多个特定于平台的实现之上提供了一个接口。这样,当开发人员只是想要一个用于哈希表的、快速健壮的哈希函数,而不需要在每个平台上都一样时,FarmHash 也能满足要求。目前,FarmHash 只包含在 32、64 和 128 位平台上用于字节数组的哈希函数。未来开发计划包含了对整数、元组和其它数据的支持。
(4) xxHash
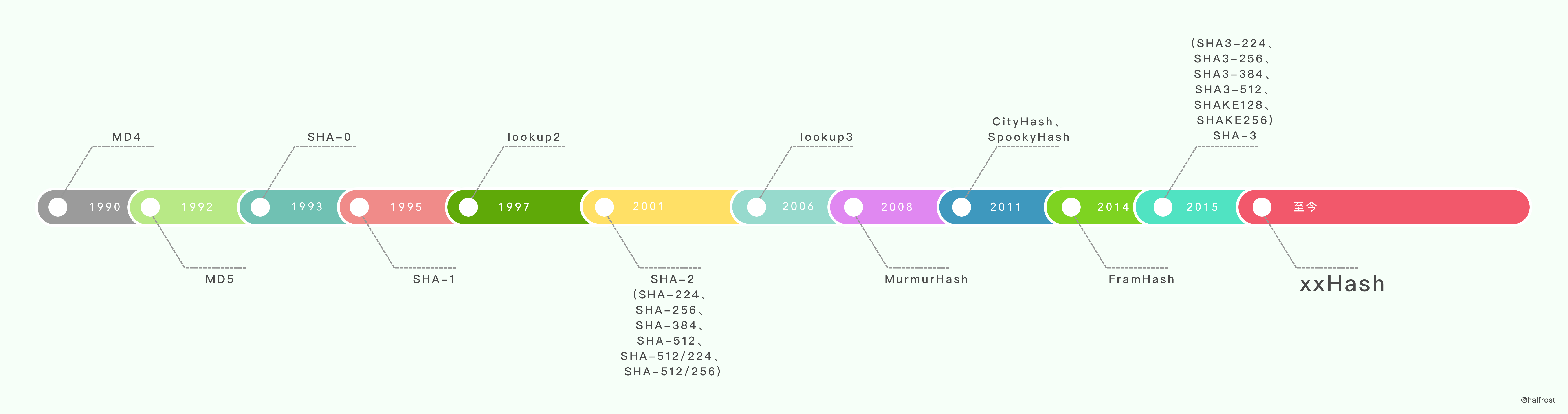
xxHash 是由 Yann Collet 创建的非加密哈希函数。它最初用于 LZ4 压缩算法,作为最终的错误检查签名的。该 hash 算法的速度接近于 RAM 的极限。并给出了 32 位和 64 位的两个版本。现在它被广泛使用在PrestoDB、RocksDB、MySQL、ArangoDB、PGroonga、Spark 这些数据库中,还用在了 Cocos2D、Dolphin、Cxbx-reloaded 这些游戏框架中,
下面这有一个性能对比的实验。测试环境是 Open-Source SMHasher program by Austin Appleby ,它是在 Windows 7 上通过 Visual C 编译出来的,并且它只有唯一一个线程。CPU 内核是 Core 2 Duo @3.0GHz。
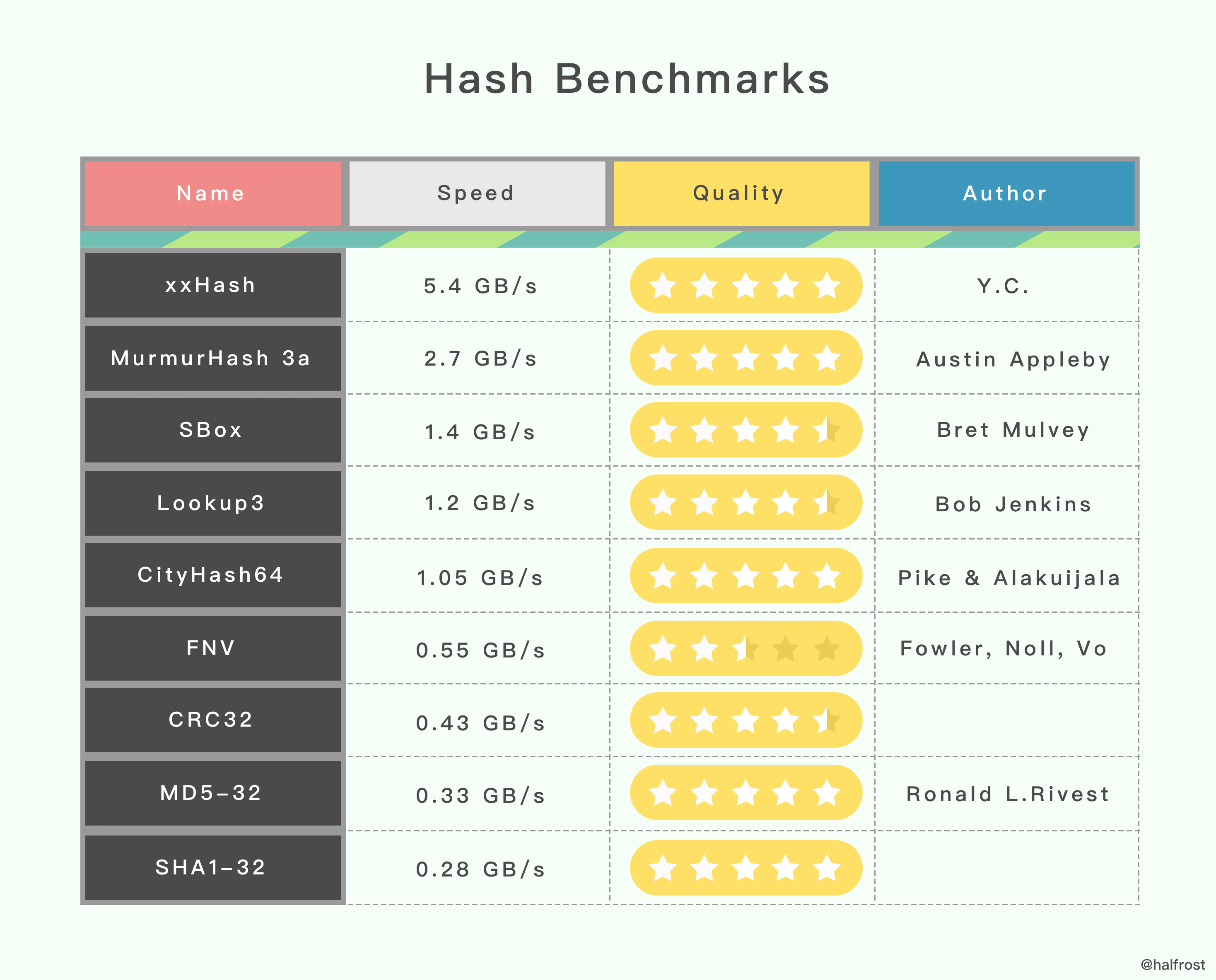
上表里面的 hash 函数并不是所有的 hash 函数,只列举了一些常见的算法。第二栏是速度的对比,可以看出来速度最快的是 xxHash 。第三栏是哈希的质量,哈希质量最高的有 5 个,全是 5 星,xxHash、MurmurHash 3a、CityHash64、MD5-32、SHA1-32 。从表里的数据看,哈希质量最高,速度最快的还是 xxHash。
(4) memhash
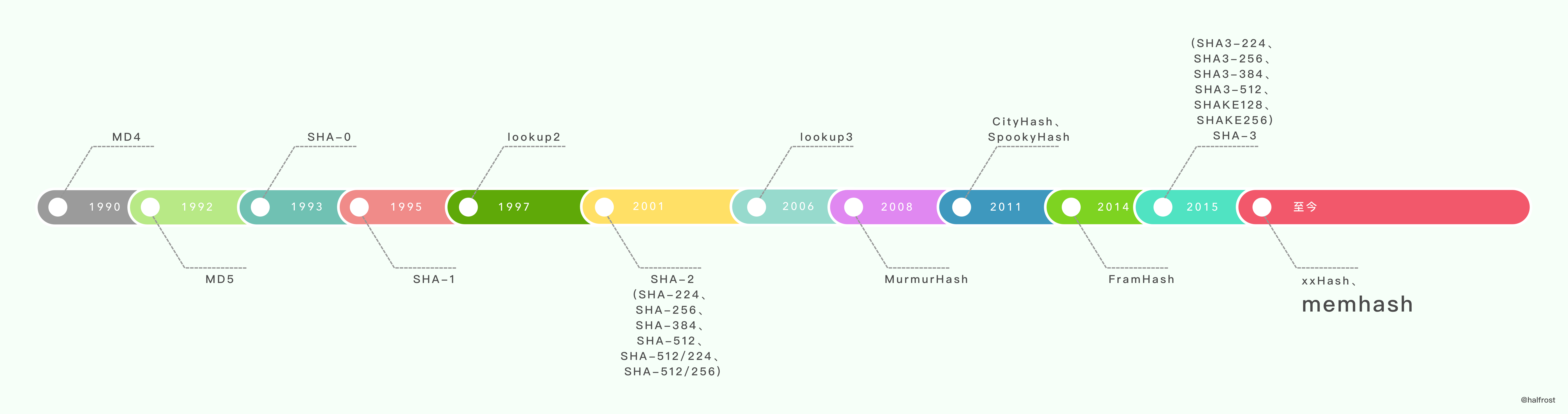
这个哈希算法笔者没有在网上找到很明确的作者信息。只在 Google 的 Go 的文档上有这么几行注释,说明了它的灵感来源:
它说 memhash 的灵感来源于 xxhash 和 cityhash。那么接下来就来看看 memhash 是怎么对字符串进行哈希的。
const (m1 = 3168982561m2 = 3339683297m3 = 832293441m4 = 2336365089)func memhash(p unsafe.Pointer, seed, s uintptr) uintptr {if GOARCH == "386" && GOOS != "nacl" && useAeshash {return aeshash(p, seed, s)}h := uint32(seed + s*hashkey[0])tail:switch {case s == 0:case s < 4:h ^= uint32(*(*byte)(p))h ^= uint32(*(*byte)(add(p, s>>1))) << 8h ^= uint32(*(*byte)(add(p, s-1))) << 16h = rotl_15(h*m1) * m2case s == 4:h ^= readUnaligned32(p)h = rotl_15(h*m1) * m2case s <= 8:h ^= readUnaligned32(p)h = rotl_15(h*m1) * m2h ^= readUnaligned32(add(p, s-4))h = rotl_15(h*m1) * m2case s <= 16:h ^= readUnaligned32(p)h = rotl_15(h*m1) * m2h ^= readUnaligned32(add(p, 4))h = rotl_15(h*m1) * m2h ^= readUnaligned32(add(p, s-8))h = rotl_15(h*m1) * m2h ^= readUnaligned32(add(p, s-4))h = rotl_15(h*m1) * m2default:v1 := hv2 := uint32(seed * hashkey[1])v3 := uint32(seed * hashkey[2])v4 := uint32(seed * hashkey[3])for s >= 16 {v1 ^= readUnaligned32(p)v1 = rotl_15(v1*m1) * m2p = add(p, 4)v2 ^= readUnaligned32(p)v2 = rotl_15(v2*m2) * m3p = add(p, 4)v3 ^= readUnaligned32(p)v3 = rotl_15(v3*m3) * m4p = add(p, 4)v4 ^= readUnaligned32(p)v4 = rotl_15(v4*m4) * m1p = add(p, 4)s -= 16}h = v1 ^ v2 ^ v3 ^ v4goto tail}h ^= h >> 17h *= m3h ^= h >> 13h *= m4h ^= h >> 16return uintptr(h)}func rotl_15(x uint32) uint32 {return (x << 15) | (x >> (32 - 15))}
m1、m2、m3、m4 是 4 个随机选的奇数,作为哈希的乘法因子。
var hashkey [4]uintptrfunc alginit() {if (GOARCH == "386" || GOARCH == "amd64") &&GOOS != "nacl" &&cpuid_ecx&(1<<25) != 0 &&cpuid_ecx&(1<<9) != 0 &&cpuid_ecx&(1<<19) != 0 {useAeshash = truealgarray[alg_MEM32].hash = aeshash32algarray[alg_MEM64].hash = aeshash64algarray[alg_STRING].hash = aeshashstrgetRandomData(aeskeysched[:])return}getRandomData((*[len(hashkey) * sys.PtrSize]byte)(unsafe.Pointer(&hashkey))[:])hashkey[0] |= 1hashkey[1] |= 1hashkey[2] |= 1hashkey[3] |= 1}
在这个初始化的函数中,初始化了 2 个数组,数组里面装的都是随机的 hashkey。在 386、 amd64、非 nacl 的平台上,会用 aeshash 。这里会把随机的 key 生成好,存入到 aeskeysched 数组中。同理,hashkey 数组里面也会随机好 4 个数字。最后都按位与了一个 1,就是为了保证生成出来的随机数都是奇数。
接下来举个例子,来看看 memhash 究竟是如何计算哈希值的。
func main() {r := [8]byte{'h', 'a', 'l', 'f', 'r', 'o', 's', 't'}pp := memhashpp(unsafe.Pointer(&r), 3, 7)fmt.Println(pp)}
为了简单起见,这里用笔者的名字为例算出哈希值,种子简单一点设置成 3。
第一步计算 h 的值。
h := uint32(seed + s*hashkey[0])
这里假设 hashkey[0] = 1,那么 h 的值为 3 + 7 * 1 = 10 。由于 s < 8,那么就会进行以下的处理:
case s <= 8:h ^= readUnaligned32(p)h = rotl_15(h*m1) * m2h ^= readUnaligned32(add(p, s-4))h = rotl_15(h*m1) * m2

readUnaligned32() 函数会把传入的 unsafe.Pointer 指针进行 2 次转换,先转成 uint32 类型,然后再转成 (*uint32) 类型。
接着进行异或操作:
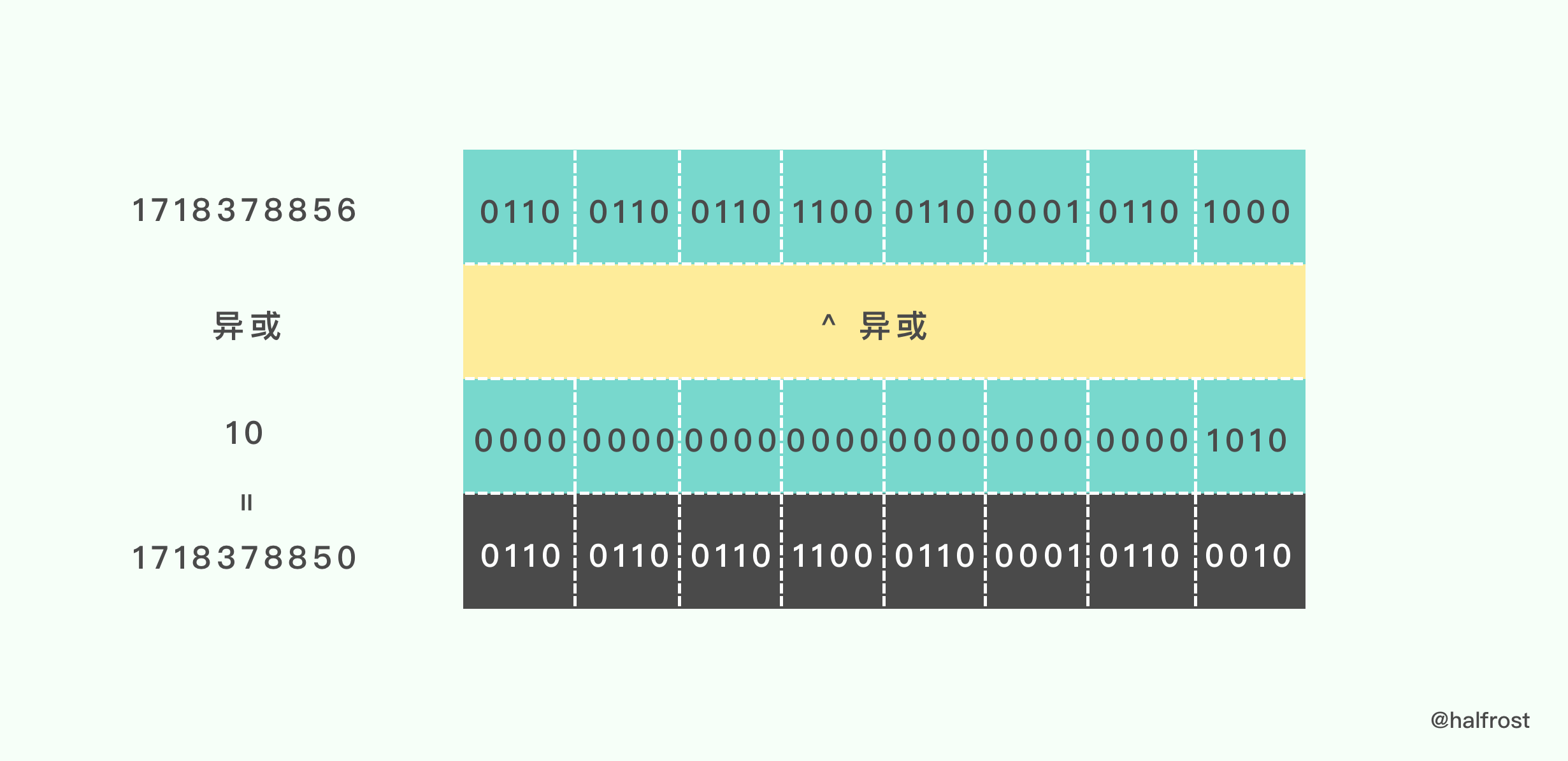
接着第二步 h m1 = 1718378850 3168982561 = 3185867170
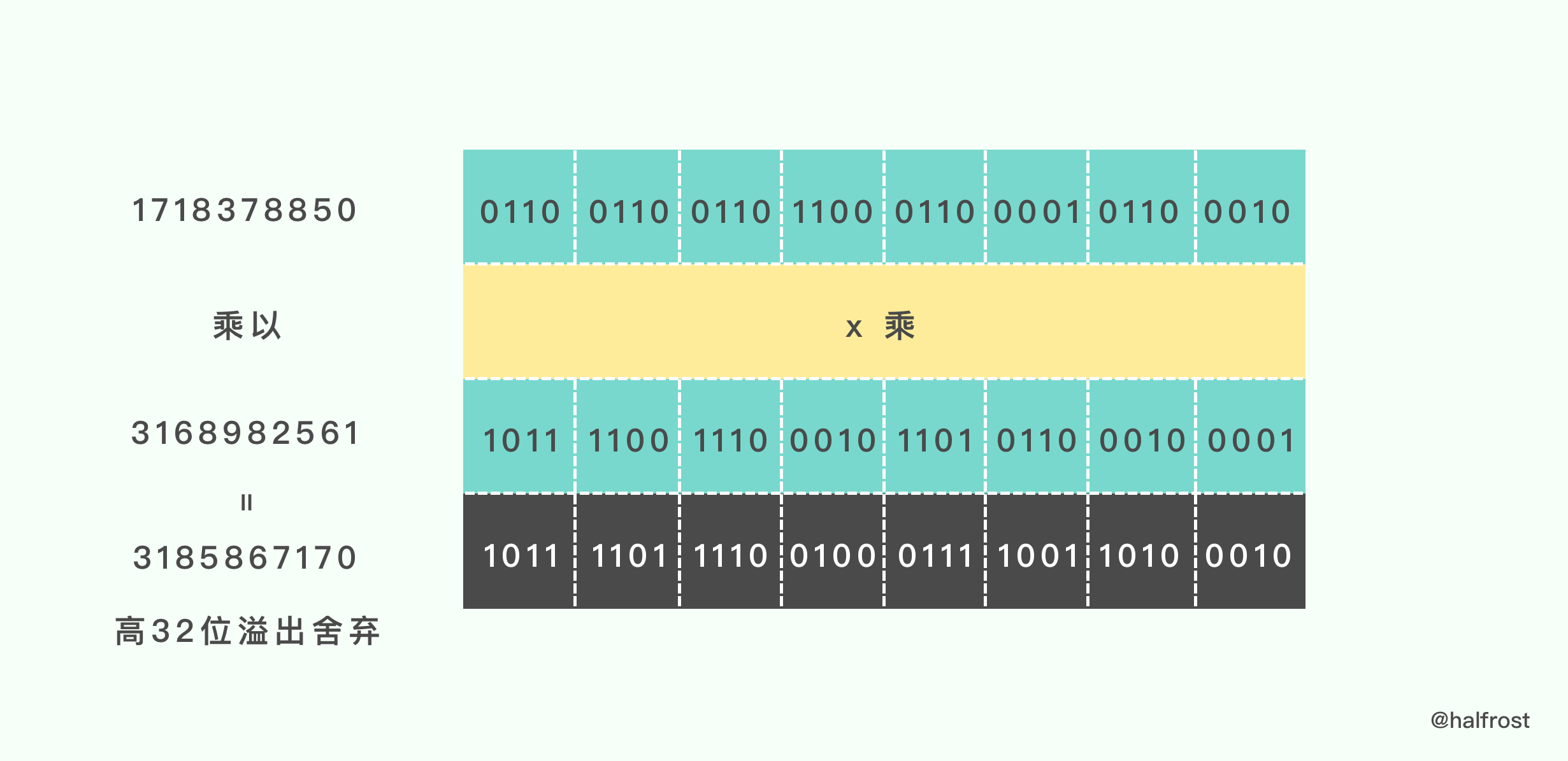
由于是 32 位的乘法,最终结果是 64 位的,高 32 位溢出,直接舍弃。
乘出来的结果当做 rotl_15() 入参。
func rotl_15(x uint32) uint32 {return (x << 15) | (x >> (32 - 15))}
这个函数里面对入参进行了两次位移操作。
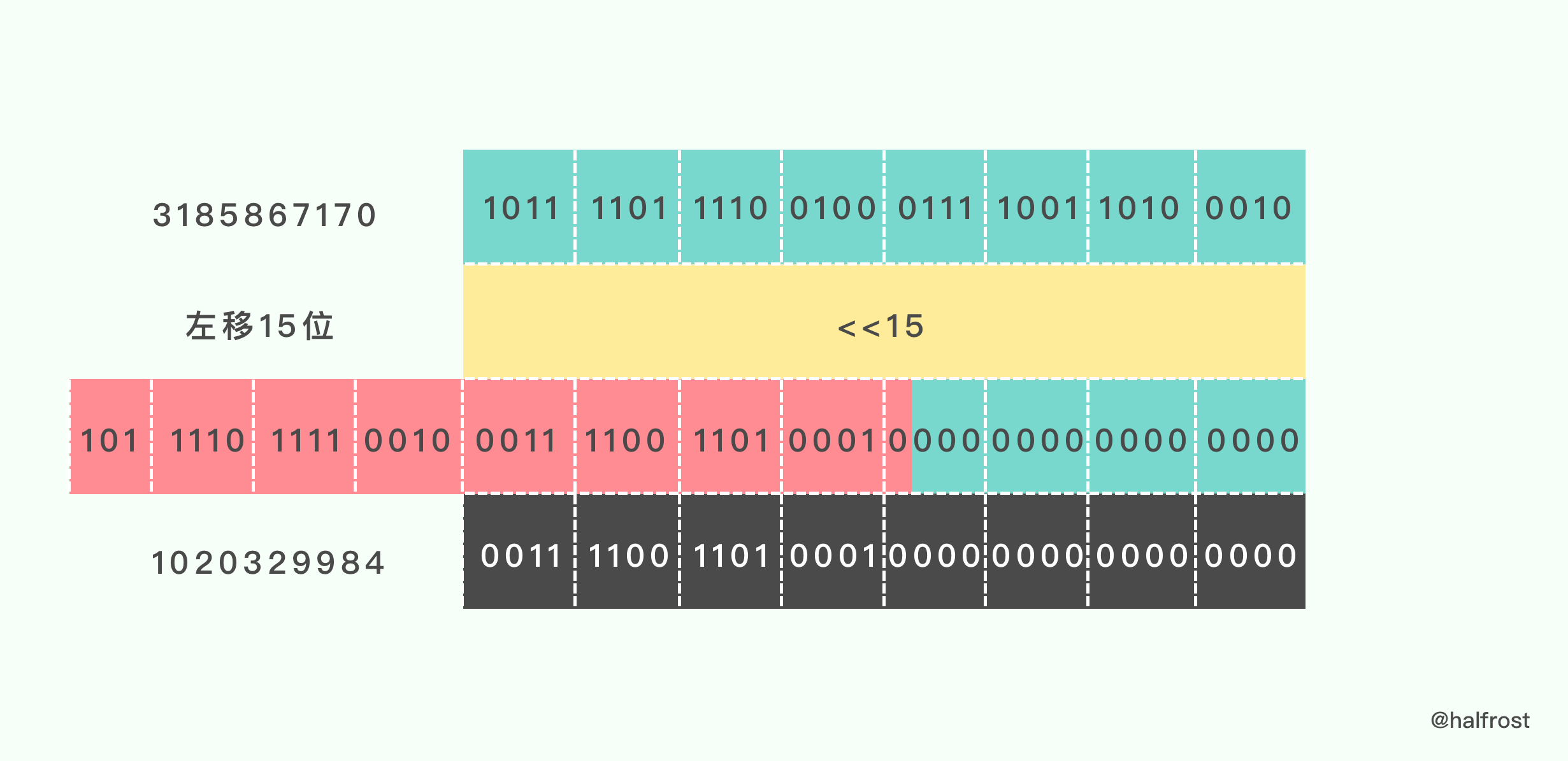

最后将两次位移的结果进行逻辑或运算:
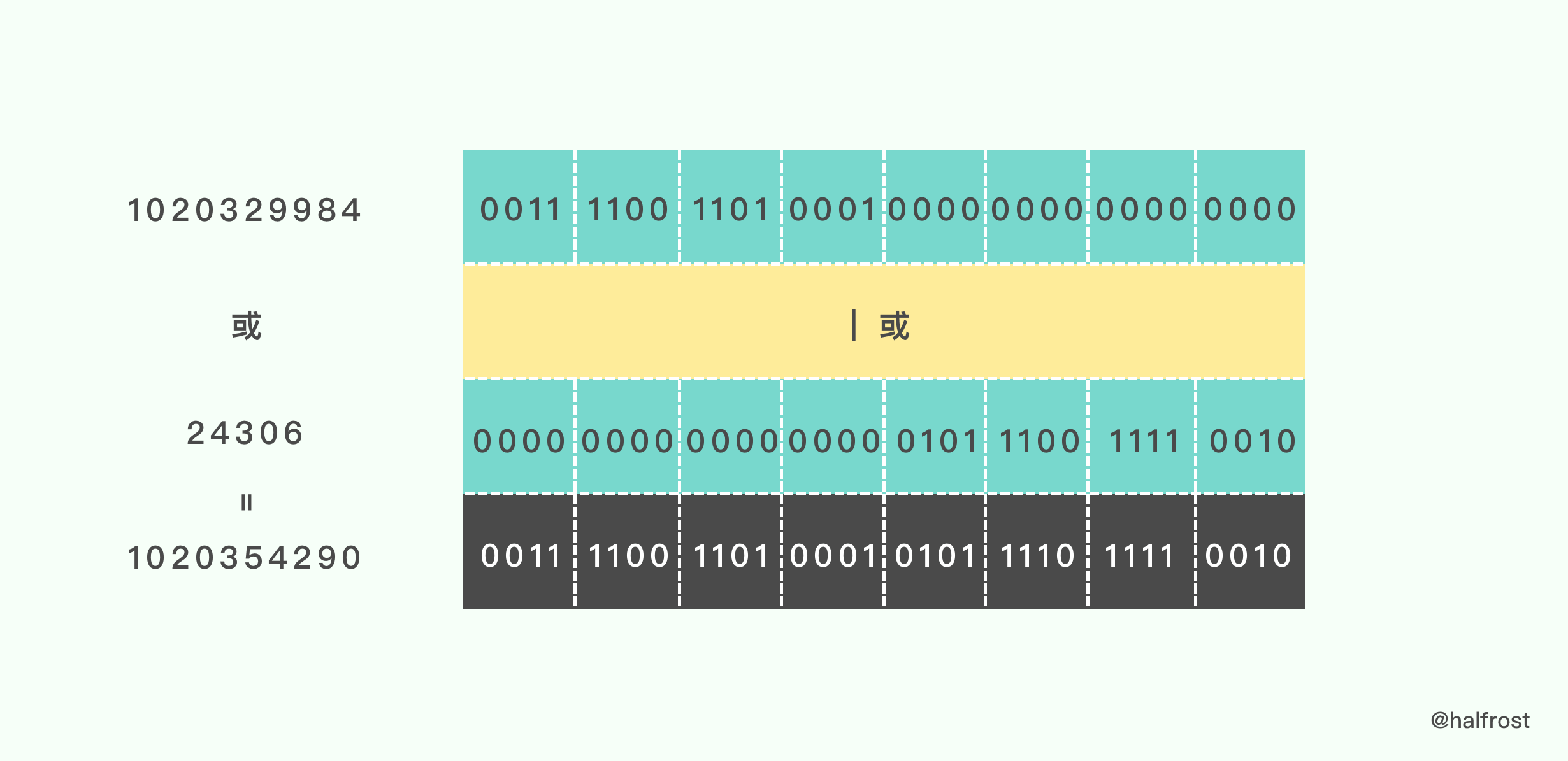
接着再进行一次 readUnaligned32() 转换:
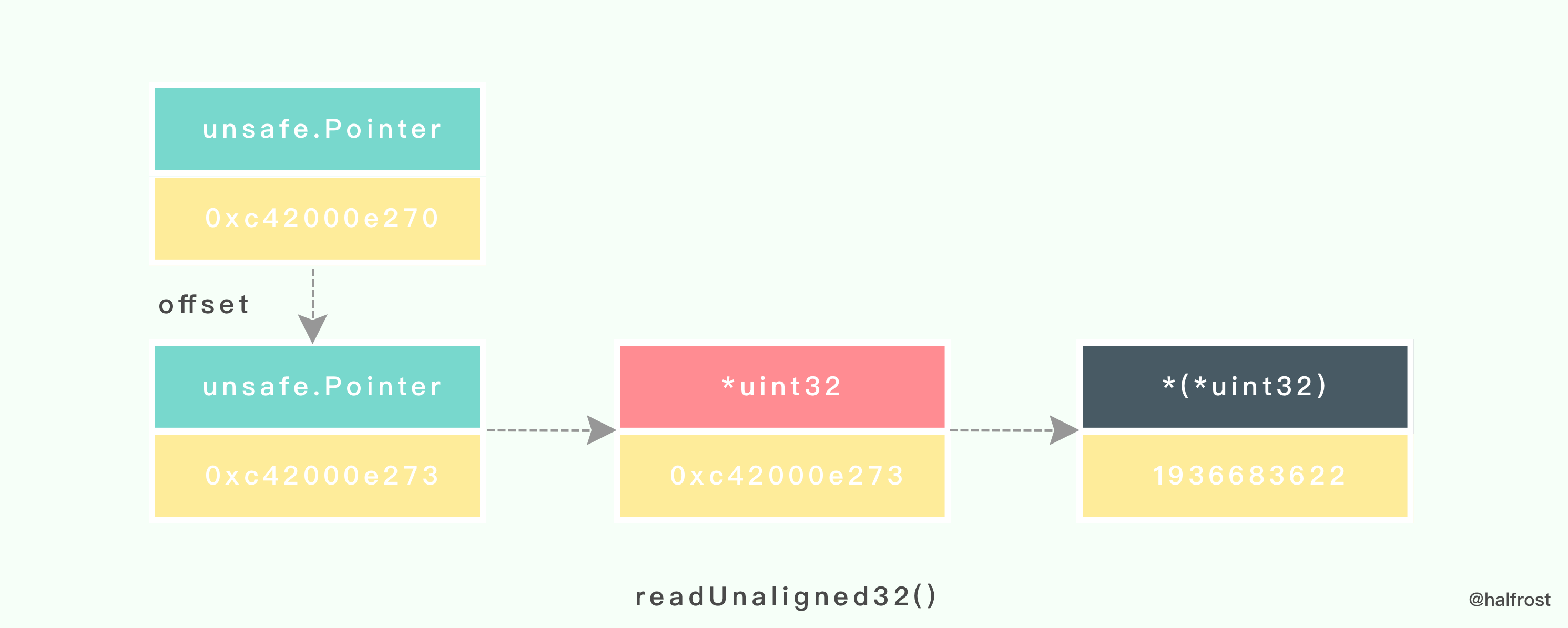
转换完再进行一次异或。此时 h = 2615762644。
然后还要再进行一次 rotl_15() 变换。这里就不画图演示了。变换完成以后 h = 2932930721。
最后执行 hash 的最后一步:
h ^= h >> 17h *= m3h ^= h >> 13h *= m4h ^= h >> 16
先右移 17 位,然后异或,再乘以 m3,再右移 13 位,再异或,再乘以 m4,再右移 16 位,最后再异或。
通过这样一系列的操作,最后就能生成出 hash 值了。最后 h = 1870717864。感兴趣的同学可以算一算。
(5)AES Hash
在上面分析 Go 的 hash 算法的时候,我们可以看到它对 CPU 是否支持 AES 指令集进行了判断,当 CPU 支持 AES 指令集的时候,它会选用 AES Hash 算法,当 CPU 不支持 AES 指令集的时候,换成 memhash 算法。
AES 指令集全称是高级加密标准指令集(或称英特尔高级加密标准新指令,简称AES-NI)是一个 x86指令集架构 的扩展,用于 Intel 和 AMD微处理器 。
利用 AES 实现 Hash 算法性能会很优秀,因为它能提供硬件加速。
具体代码实现如下,汇编程序,注释见下面程序中:
TEXT runtime·aeshash(SB),NOSPLIT,$0-32MOVQ p+0(FP), AXMOVQ s+16(FP), CXLEAQ ret+24(FP), DXJMP runtime·aeshashbody(SB)TEXT runtime·aeshashstr(SB),NOSPLIT,$0-24MOVQ p+0(FP), AXMOVQ 8(AX), CXMOVQ (AX), AXLEAQ ret+16(FP), DXJMP runtime·aeshashbody(SB)
最终的 hash 的实现都在 aeshashbody 中:
TEXT runtime·aeshashbody(SB),NOSPLIT,$0-0MOVQ h+8(FP), X0PINSRW $4, CX, X0PSHUFHW $0, X0, X0MOVO X0, X1PXOR runtime·aeskeysched(SB), X0AESENC X0, X0CMPQ CX, $16JB aes0to15JE aes16CMPQ CX, $32JBE aes17to32CMPQ CX, $64JBE aes33to64CMPQ CX, $128JBE aes65to128JMP aes129plusaes0to15:TESTQ CX, CXJE aes0ADDQ $16, AXTESTW $0xff0, AXJE endofpageMOVOU -16(AX), X1ADDQ CX, CXMOVQ $masks<>(SB), AXPAND (AX)(CX*8), X1final1:PXOR X0, X1AESENC X1, X1AESENC X1, X1AESENC X1, X1MOVQ X1, (DX)RETendofpage:MOVOU -32(AX)(CX*1), X1ADDQ CX, CXMOVQ $shifts<>(SB), AXPSHUFB (AX)(CX*8), X1JMP final1aes0:AESENC X0, X0MOVQ X0, (DX)RETaes16:MOVOU (AX), X1JMP final1aes17to32:PXOR runtime·aeskeysched+16(SB), X1AESENC X1, X1MOVOU (AX), X2MOVOU -16(AX)(CX*1), X3PXOR X0, X2PXOR X1, X3AESENC X2, X2AESENC X3, X3AESENC X2, X2AESENC X3, X3AESENC X2, X2AESENC X3, X3PXOR X3, X2MOVQ X2, (DX)RETaes33to64:MOVO X1, X2MOVO X1, X3PXOR runtime·aeskeysched+16(SB), X1PXOR runtime·aeskeysched+32(SB), X2PXOR runtime·aeskeysched+48(SB), X3AESENC X1, X1AESENC X2, X2AESENC X3, X3MOVOU (AX), X4MOVOU 16(AX), X5MOVOU -32(AX)(CX*1), X6MOVOU -16(AX)(CX*1), X7PXOR X0, X4PXOR X1, X5PXOR X2, X6PXOR X3, X7AESENC X4, X4AESENC X5, X5AESENC X6, X6AESENC X7, X7AESENC X4, X4AESENC X5, X5AESENC X6, X6AESENC X7, X7AESENC X4, X4AESENC X5, X5AESENC X6, X6AESENC X7, X7PXOR X6, X4PXOR X7, X5PXOR X5, X4MOVQ X4, (DX)RETaes65to128:MOVO X1, X2MOVO X1, X3MOVO X1, X4MOVO X1, X5MOVO X1, X6MOVO X1, X7PXOR runtime·aeskeysched+16(SB), X1PXOR runtime·aeskeysched+32(SB), X2PXOR runtime·aeskeysched+48(SB), X3PXOR runtime·aeskeysched+64(SB), X4PXOR runtime·aeskeysched+80(SB), X5PXOR runtime·aeskeysched+96(SB), X6PXOR runtime·aeskeysched+112(SB), X7AESENC X1, X1AESENC X2, X2AESENC X3, X3AESENC X4, X4AESENC X5, X5AESENC X6, X6AESENC X7, X7MOVOU (AX), X8MOVOU 16(AX), X9MOVOU 32(AX), X10MOVOU 48(AX), X11MOVOU -64(AX)(CX*1), X12MOVOU -48(AX)(CX*1), X13MOVOU -32(AX)(CX*1), X14MOVOU -16(AX)(CX*1), X15PXOR X0, X8PXOR X1, X9PXOR X2, X10PXOR X3, X11PXOR X4, X12PXOR X5, X13PXOR X6, X14PXOR X7, X15AESENC X8, X8AESENC X9, X9AESENC X10, X10AESENC X11, X11AESENC X12, X12AESENC X13, X13AESENC X14, X14AESENC X15, X15AESENC X8, X8AESENC X9, X9AESENC X10, X10AESENC X11, X11AESENC X12, X12AESENC X13, X13AESENC X14, X14AESENC X15, X15AESENC X8, X8AESENC X9, X9AESENC X10, X10AESENC X11, X11AESENC X12, X12AESENC X13, X13AESENC X14, X14AESENC X15, X15PXOR X12, X8PXOR X13, X9PXOR X14, X10PXOR X15, X11PXOR X10, X8PXOR X11, X9PXOR X9, X8MOVQ X8, (DX)RETaes129plus:MOVO X1, X2MOVO X1, X3MOVO X1, X4MOVO X1, X5MOVO X1, X6MOVO X1, X7PXOR runtime·aeskeysched+16(SB), X1PXOR runtime·aeskeysched+32(SB), X2PXOR runtime·aeskeysched+48(SB), X3PXOR runtime·aeskeysched+64(SB), X4PXOR runtime·aeskeysched+80(SB), X5PXOR runtime·aeskeysched+96(SB), X6PXOR runtime·aeskeysched+112(SB), X7AESENC X1, X1AESENC X2, X2AESENC X3, X3AESENC X4, X4AESENC X5, X5AESENC X6, X6AESENC X7, X7MOVOU -128(AX)(CX*1), X8MOVOU -112(AX)(CX*1), X9MOVOU -96(AX)(CX*1), X10MOVOU -80(AX)(CX*1), X11MOVOU -64(AX)(CX*1), X12MOVOU -48(AX)(CX*1), X13MOVOU -32(AX)(CX*1), X14MOVOU -16(AX)(CX*1), X15PXOR X0, X8PXOR X1, X9PXOR X2, X10PXOR X3, X11PXOR X4, X12PXOR X5, X13PXOR X6, X14PXOR X7, X15DECQ CXSHRQ $7, CXaesloop:AESENC X8, X8AESENC X9, X9AESENC X10, X10AESENC X11, X11AESENC X12, X12AESENC X13, X13AESENC X14, X14AESENC X15, X15MOVOU (AX), X0MOVOU 16(AX), X1MOVOU 32(AX), X2MOVOU 48(AX), X3AESENC X0, X8AESENC X1, X9AESENC X2, X10AESENC X3, X11MOVOU 64(AX), X4MOVOU 80(AX), X5MOVOU 96(AX), X6MOVOU 112(AX), X7AESENC X4, X12AESENC X5, X13AESENC X6, X14AESENC X7, X15ADDQ $128, AXDECQ CXJNE aesloopAESENC X8, X8AESENC X9, X9AESENC X10, X10AESENC X11, X11AESENC X12, X12AESENC X13, X13AESENC X14, X14AESENC X15, X15AESENC X8, X8AESENC X9, X9AESENC X10, X10AESENC X11, X11AESENC X12, X12AESENC X13, X13AESENC X14, X14AESENC X15, X15AESENC X8, X8AESENC X9, X9AESENC X10, X10AESENC X11, X11AESENC X12, X12AESENC X13, X13AESENC X14, X14AESENC X15, X15PXOR X12, X8PXOR X13, X9PXOR X14, X10PXOR X15, X11PXOR X10, X8PXOR X11, X9PXOR X9, X8MOVQ X8, (DX)RET
2. 哈希冲突处理
(1)链表数组法
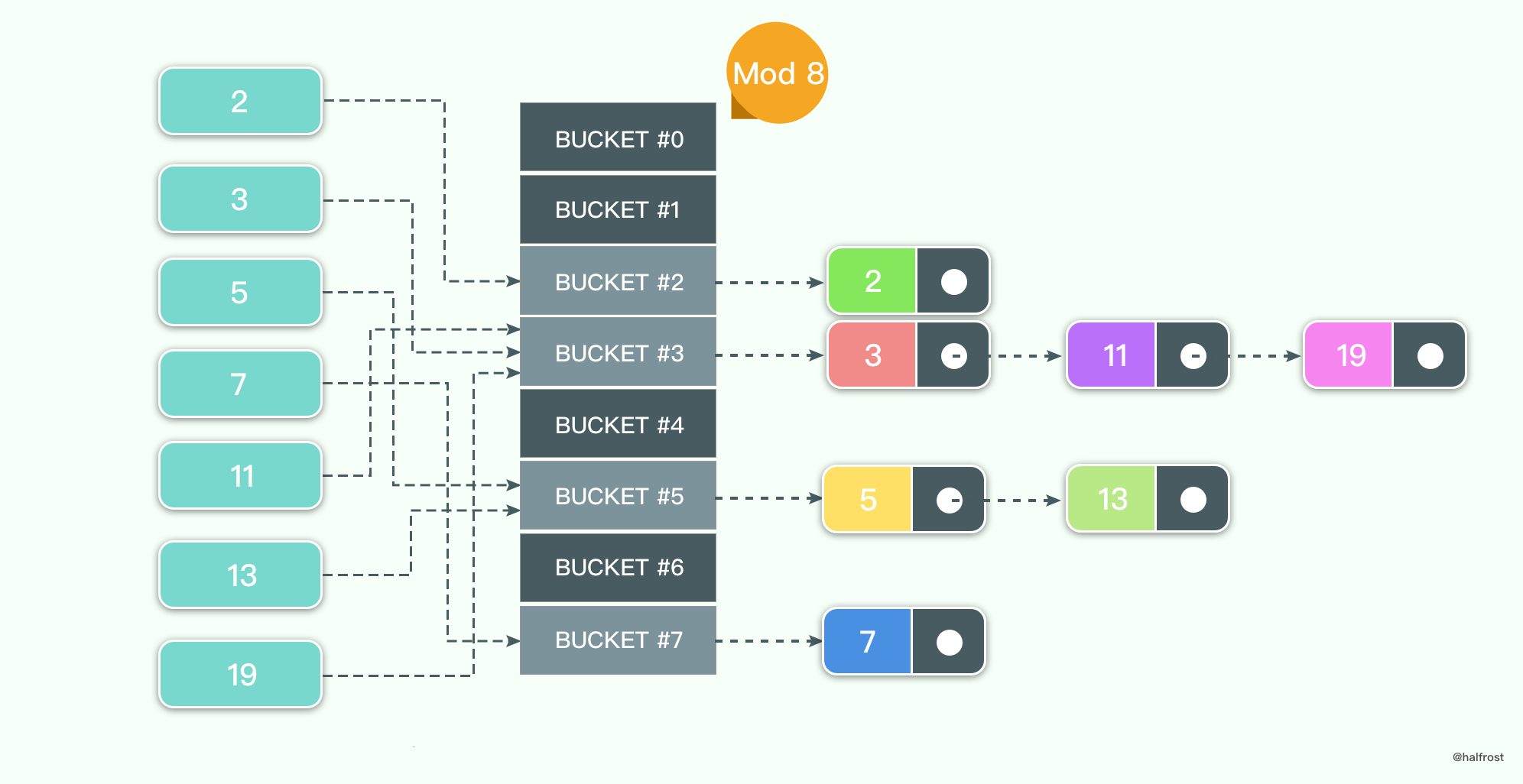
链表数组法比较简单,每个键值对表长取模,如果结果相同,用链表的方式依次往后插入。
假设待插入的键值集合是 {2,3,5,7,11,13,19},表长 MOD 8。假设哈希函数在[0,9) 上均匀分布。如上图。
接下来重点进行性能分析:
查找键值 k,假设键值 k 不在哈希表中,h(k) 在 [0,M) 中均匀分布,即 P(h(k) = i) = 1/M 。令 Xi 为哈希表 ht[ i ] 中包含键值的个数。如果 h(k) = i ,则不成功查找 k 的键值比较次数是 Xi,于是:
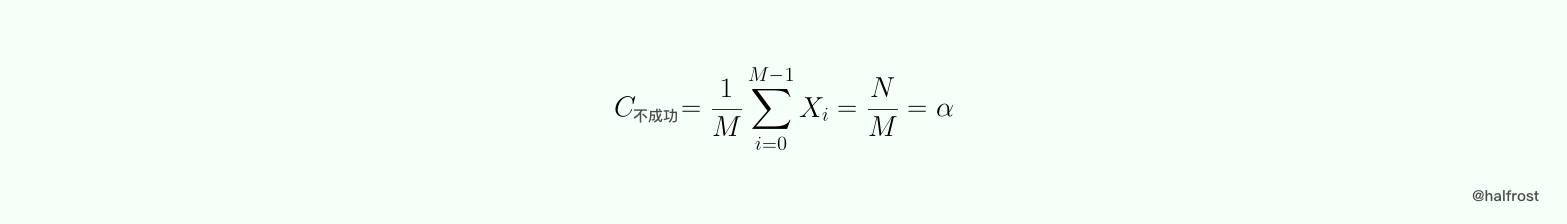
成功查找的分析稍微复杂一点。要考虑添加哈希表的次序,不考虑有相同键值的情况,假设 K = {k1,k2,……kn},并且假设从空哈希表开始按照这个次序添加到哈希表中。引入随机变量,如果 h(ki) = h(kj),那么 Xij = 1;如果 h(ki) != h(kj),那么 Xij = 0 。
由于之前的假设哈希表是均匀分布的,所以 P(Xij = i) = E(Xij) = 1/M ,这里的 E(X) 表示随机变量 X 的数学期望。再假设每次添加键值的时候都是把添加在链表末端。令 Ci 为查找 Ki 所需的键值比较次数,由于不能事先确定查找 Ki 的概率,所以假定查找不同键值的概率都是相同的,都是 1/n ,则有:
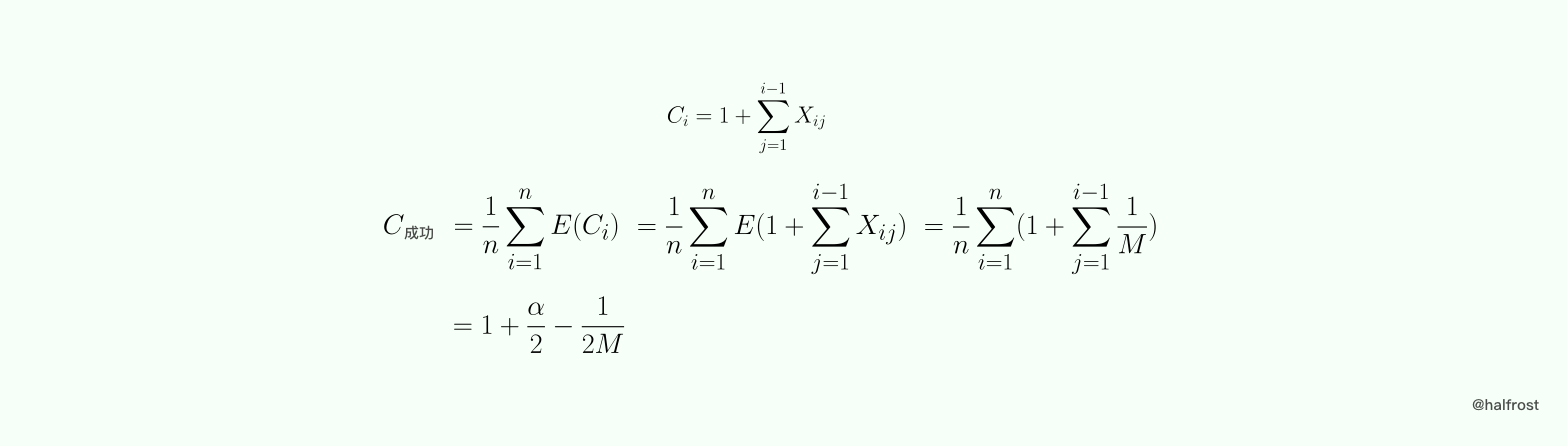
由此我们可以看出,哈希表的性能和表中元素的多少关系不大,而和填充因子 α 有关。如果哈希表长和哈希表中元素个数成正比,则哈希表查找的复杂度为 O(1) 。
综上所述,链表数组的成功与不成功的平均键值比较次数如下:
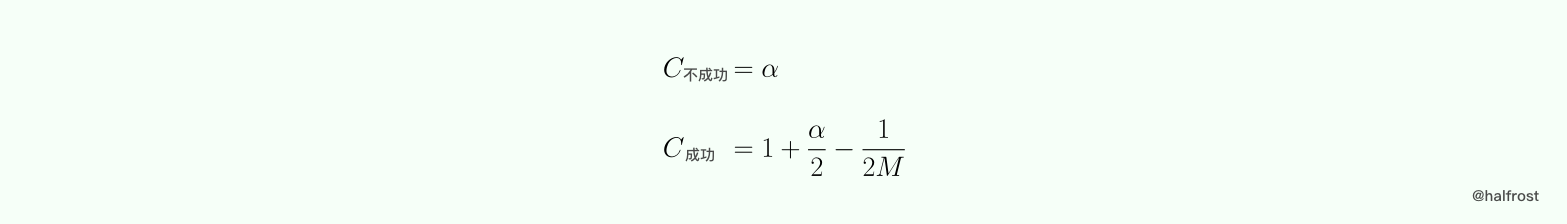
(2)开放地址法 —— 线性探测
线性探测的规则是 hi = (h(k) + i ) MOD M。举个例子,i = 1,M = 9。
这种处理冲突的方法,一旦发生冲突,就把位置往后加 1,直到找到一个空的位置。
举例如下,假设待插入的键值集合是 {2,3,5,7,11,13,19},线性探测的发生冲突以后添加的值为 1,那么最终结果如下:
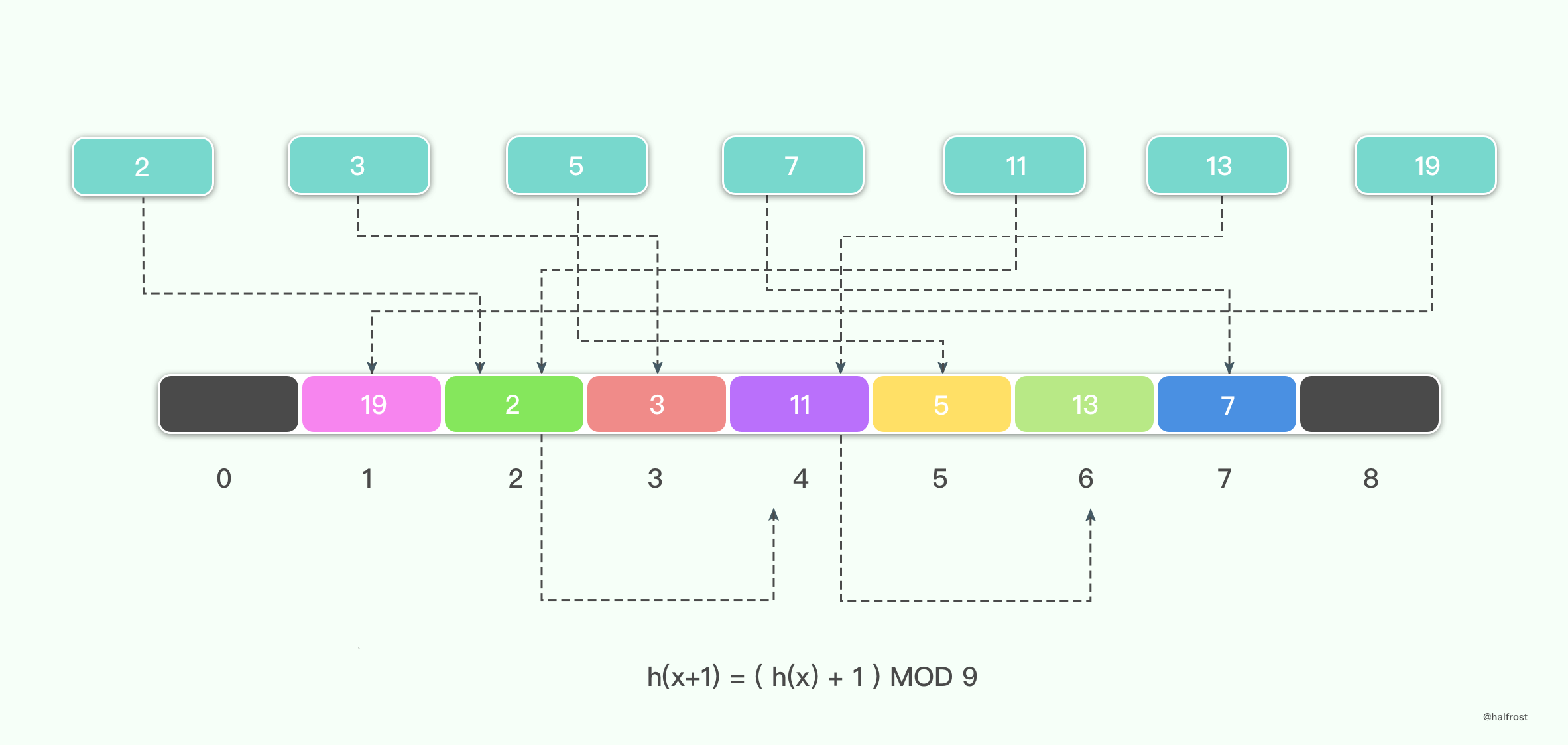
线性探测哈希表的性能分析比较复杂,这里就仅给出结果。
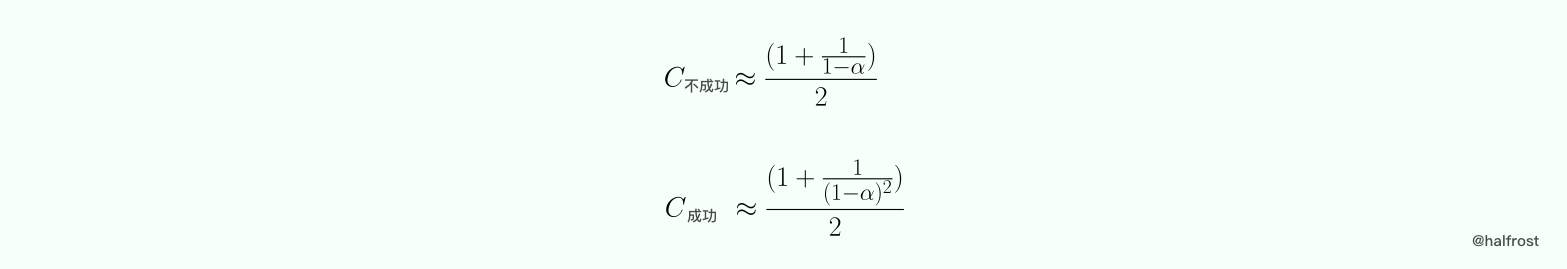
(3)开放地址法 —— 平方探测
线性探测的规则是 h0 = h(k) ,hi = ( h0 + i * i ) MOD M。
举例如下,假设待插入的键值集合是 {2,3,5,7,11,13,20},平方探测的发生冲突以后添加的值为查找次数的平方,那么最终结果如下:
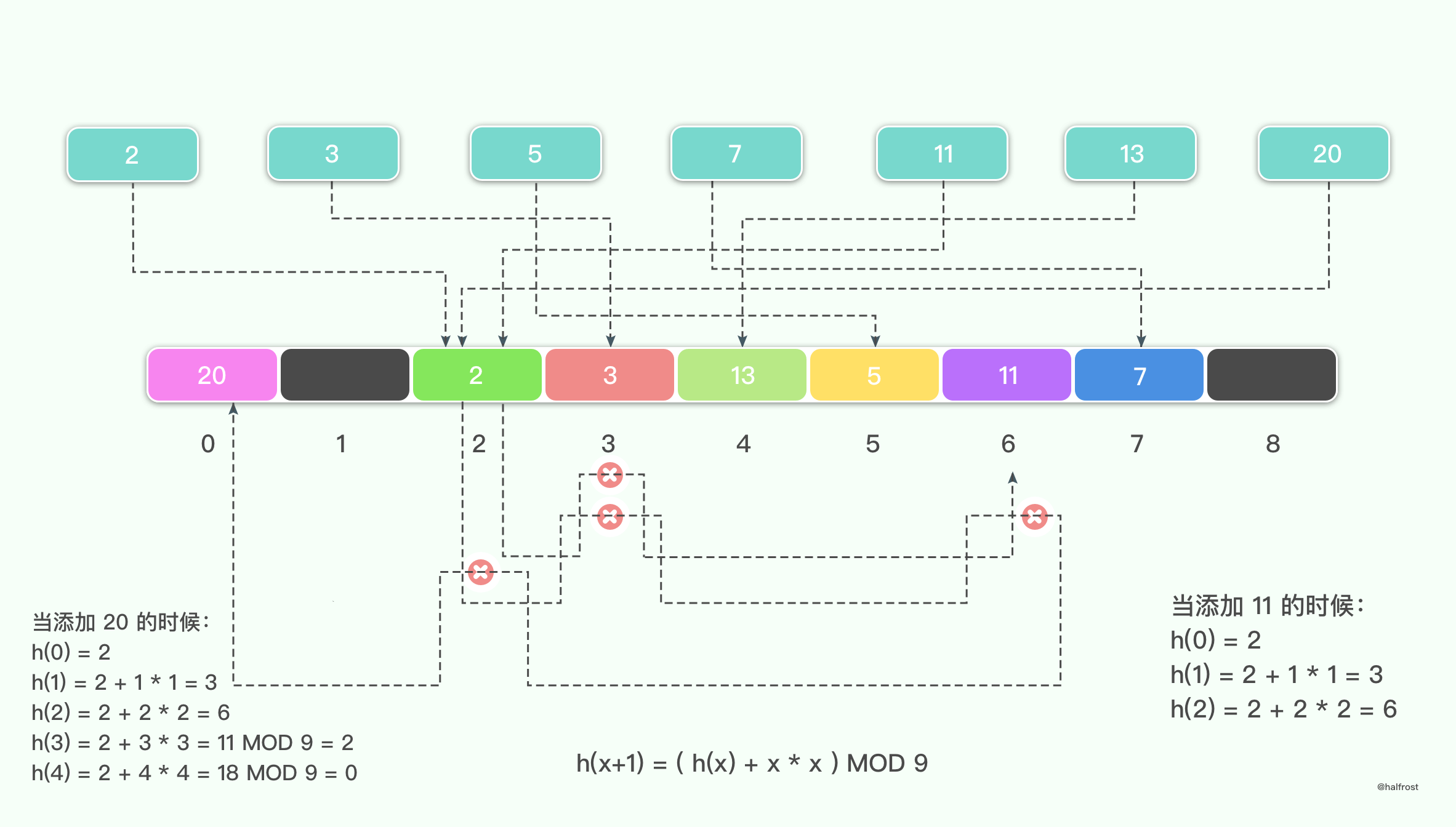
平方探测在线性探测的基础上,加了一个二次曲线。当发生冲突以后,不再是加一个线性的参数,而是加上探测次数的平方。
平方探测有一个需要注意的是,M 的大小有讲究。如果 M 不是奇素数,那么就可能出现下面这样的问题,即使哈希表里面还有空的位置,但是却有元素找不到要插入的位置。
举例,假设 M = 10,待插入的键值集合是 {0,1,4,5,6,9,10},当前面 6 个键值插入哈希表中以后,10 就再也无法插入了。
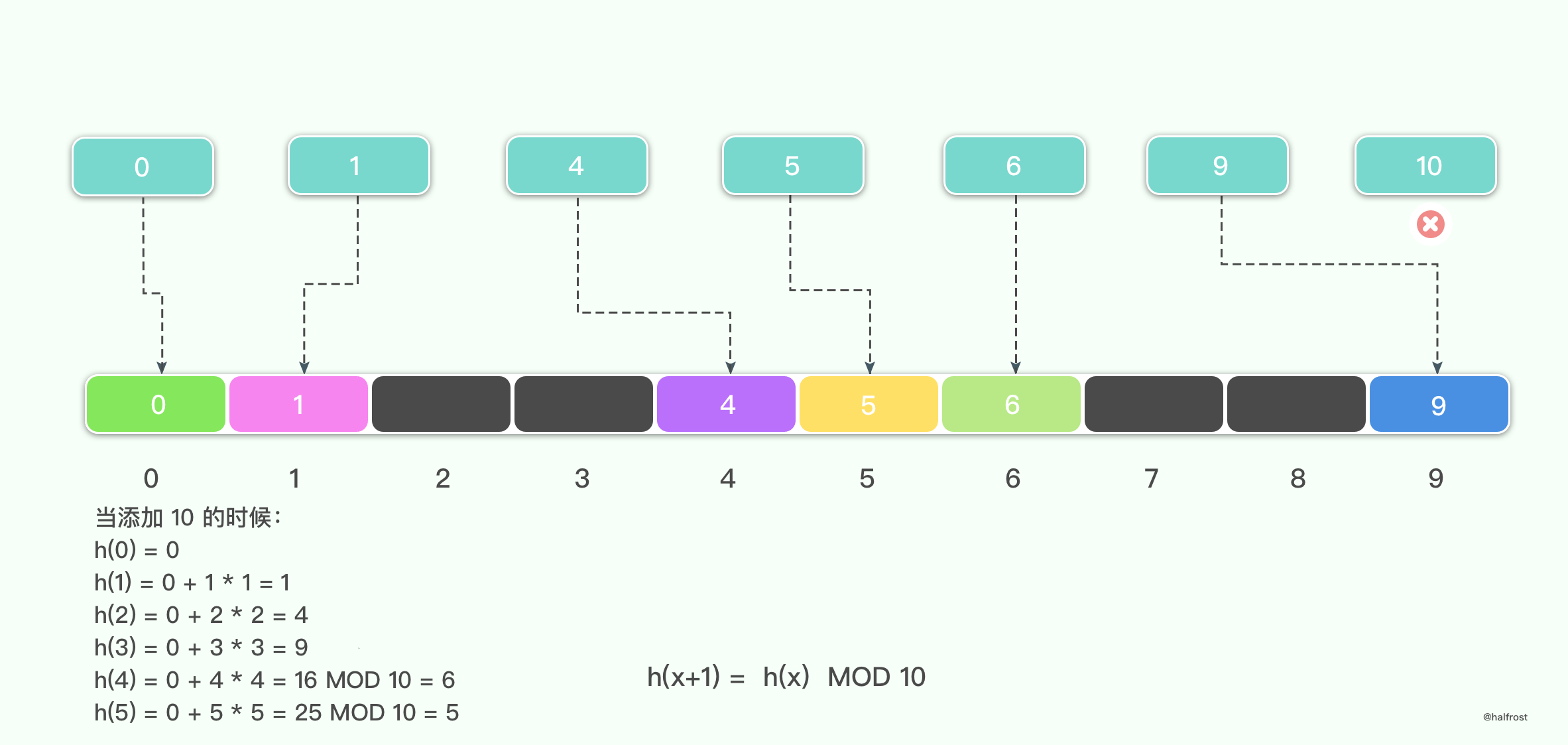
所以在平方探测中,存在下面这则规律:
如果 M 为奇素数,则下面的 ⌈M / 2⌉ 位置 h0,h1,h2 …… h⌊M/2⌋ 互不相同。其中,hi = (h0 + i * i ) MOD M。
这面这则规律可以用反证法证明。假设 hi = hj,i > j;0<=i,j<= ⌊M/2⌋,则 h0 + i i = ( h0 + j j ) MOD M,从而 M 可以整除 (i + j)( i - j )。由于 M 为素数,并且 0 < i + j,i - j < M,当且仅当 i = j 的时候才能满足。
上述规则也就说明了一点,只要 M 为奇素数,平方探测至少可以遍历哈希表一般的位置。所以只要哈希表的填充因子 α <= 1 / 2 ,平方探测总能找到可插入的位置。
上述举的例子,之所以键值 10 无法插入,原因也因为 α > 1 / 2 了,所以不能保证有可插入的位置了。
(4)开放地址法 —— 双哈希探测
双哈希探测是为了解决聚集的现象。无论是线性探测还是平方探测,如果 h(k1) 和 h(k2) 相邻,则它们的探测序列也都是相邻的,这就是所谓的聚集现象。为了避免这种现象,所以引入了双哈希函数 h2,使得两次探测之间的距离为 h2(k)。所以探测序列为 h0 = h1(k),hi = ( h0 + i * h2(k) ) MOD M 。实验表明,双哈希探测的性能类似于随机探测。
关于双哈希探测和平方探测的平均查找长度比线性探测更加困难。所以引入随机探测的概念来近似这两种探测。随机探测是指探测序列 {hi} 在区间 [0,M]中等概率独立随机选取,这样 P(hi = j) = 1/M 。
假设探测序列为 h0,h1,……,hi。在哈希表的 hi 位置为空,在 h0,h1,……,hi-1 的位置上哈希表不是空,此次查找的键值比较次数为 i。令随机变量 X 为一次不成功查找所需的键值比较次数。由于哈希表的填充因子为 α,所以在一个位置上哈希表为空值的概率为 1 - α ,为非空值的概率为 α,所以 P(X = i) = α^i * (1 - α) 。
在概率论中,上述的分布叫几何分布。
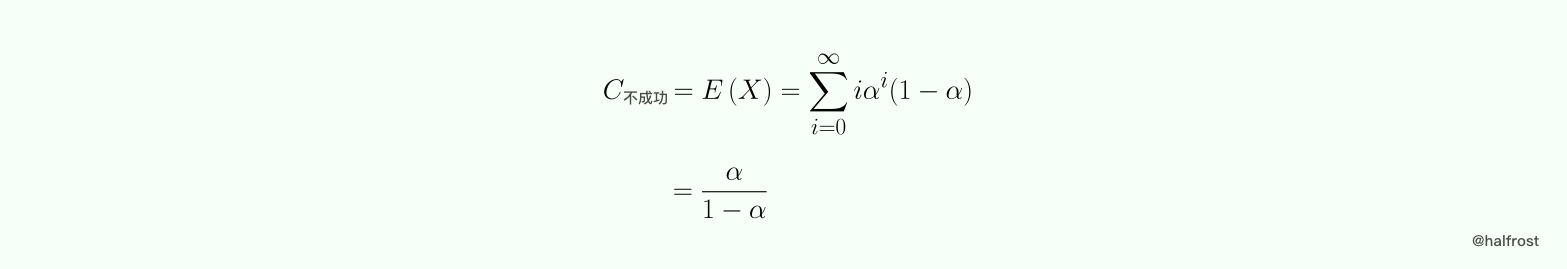
假定哈希表元素的添加顺序为 {k1,k2,…… ,kn},令 Xi 为当哈希表只包含 {k1,k2,…… ,ki} 时候一次不成功查找的键值比较次数,注意,这个时候哈希表的填充因子为 i/M ,则查找 k(i+1) 的键值次数为 Yi = 1 + Xi。假定查找任意一个键值的概率为 1/n,则一次成功查找的平均键值比较次数为:
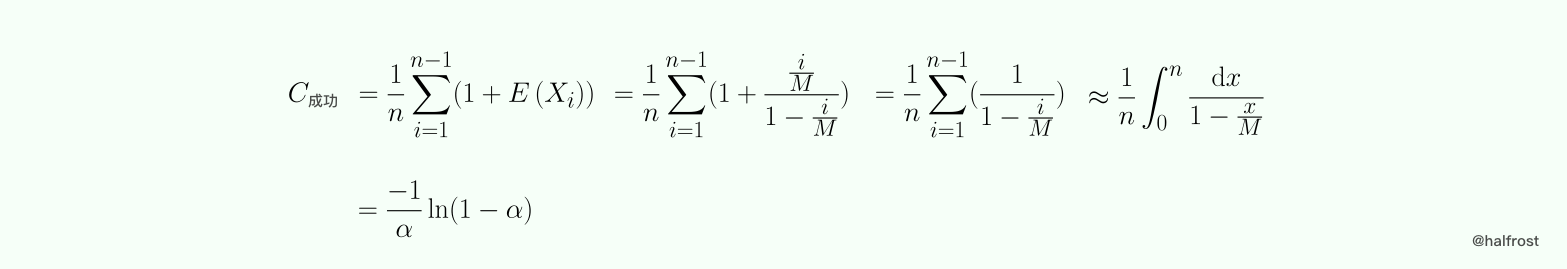
综上所述,平方探测和双哈希探测的成功与不成功的平均键值比较次数如下:
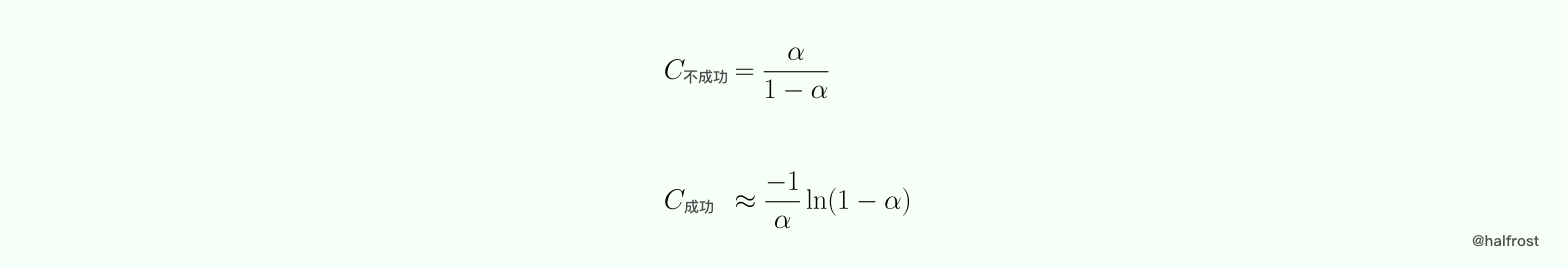
总的来说,在数据量非常大的情况下,简单的 hash 函数不可避免不产生碰撞,即使采用了合适的处理碰撞的方法,依旧有一定时间复杂度。所以想尽可能的避免碰撞,还是要选择高性能的 hash 函数,或者增加 hash 的位数,比如 64 位,128 位,256 位,这样碰撞的几率会小很多。
3. 哈希表的扩容策略
随着哈希表装载因子的变大,发生碰撞的次数变得越来也多,哈希表的性能变得越来越差。对于单独链表法实现的哈希表,尚可以容忍,但是对于开放寻址法,这种性能的下降是不能接受的,因此对于开放寻址法需要寻找一种方法解决这个问题。
在实际应用中,解决这个问题的办法是动态的增大哈希表的长度,当装载因子超过某个阈值时增加哈希表的长度,自动扩容。每当哈希表的长度发生变化之后,所有 key 在哈希表中对应的下标索引需要全部重新计算,不能直接从原来的哈希表中拷贝到新的哈希表中。必须一个一个计算原来哈希表中的 key 的哈希值并插入到新的哈希表中。这种方式肯定是达不到生产环境的要求的,因为时间复杂度太高了,O(n),数据量一旦大了,性能就会很差。Redis 想了一种方法,就算是触发增长时也只需要常数时间 O(1) 即可完成插入操作。解决办法是分多次、渐进式地完成的旧哈希表到新哈希表的拷贝而不是一次拷贝完成。
接下来以 Redis 为例,来谈谈它是哈希表是如何进行扩容并且不太影响性能的。
Redis 对字典的定义如下:
typedef struct dict {dictType *type;void *privdata;dictht ht[2];int rehashidx;int iterators;} dict;
从定义上我们可以看到,Redis 字典保存了 2 个哈希表,哈希表 ht[1]就是用来 rehash 的。
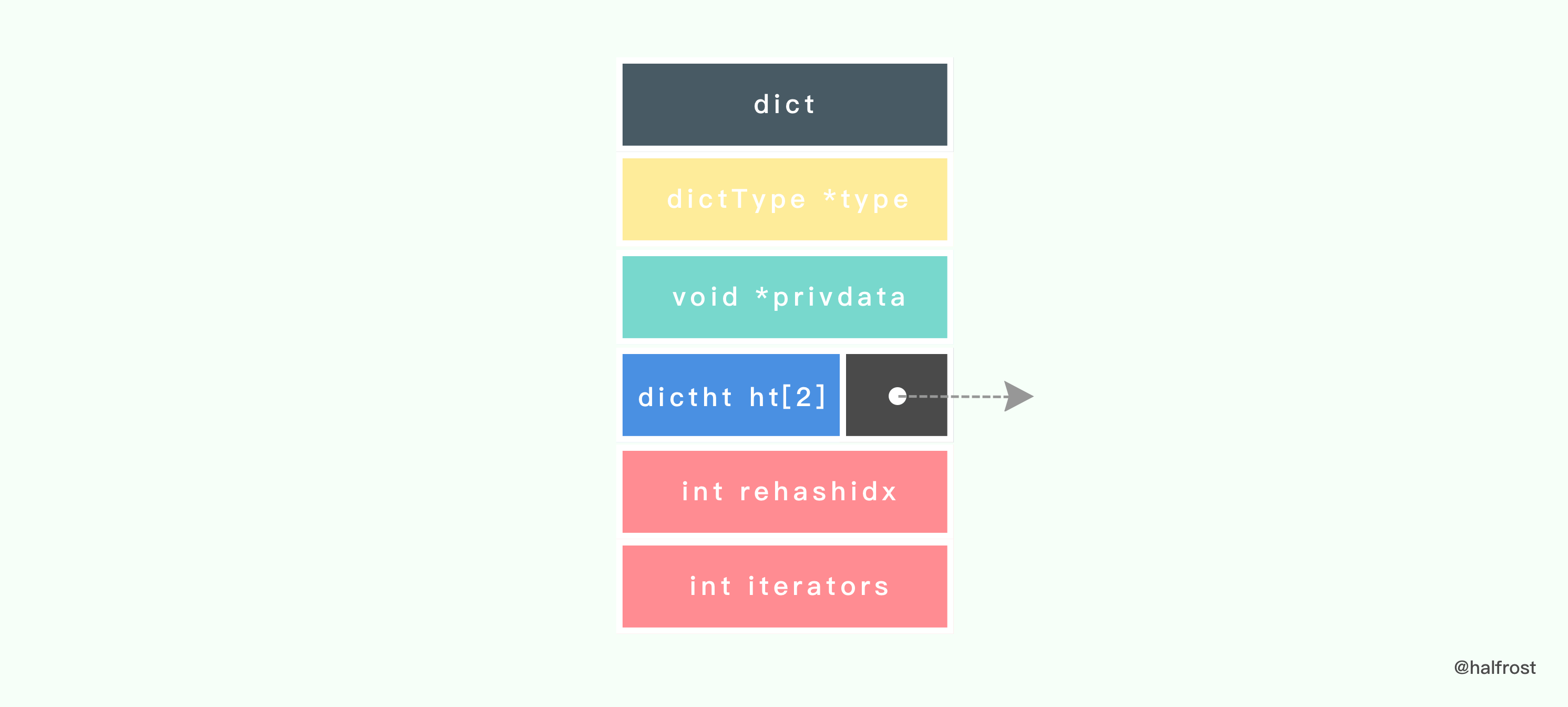
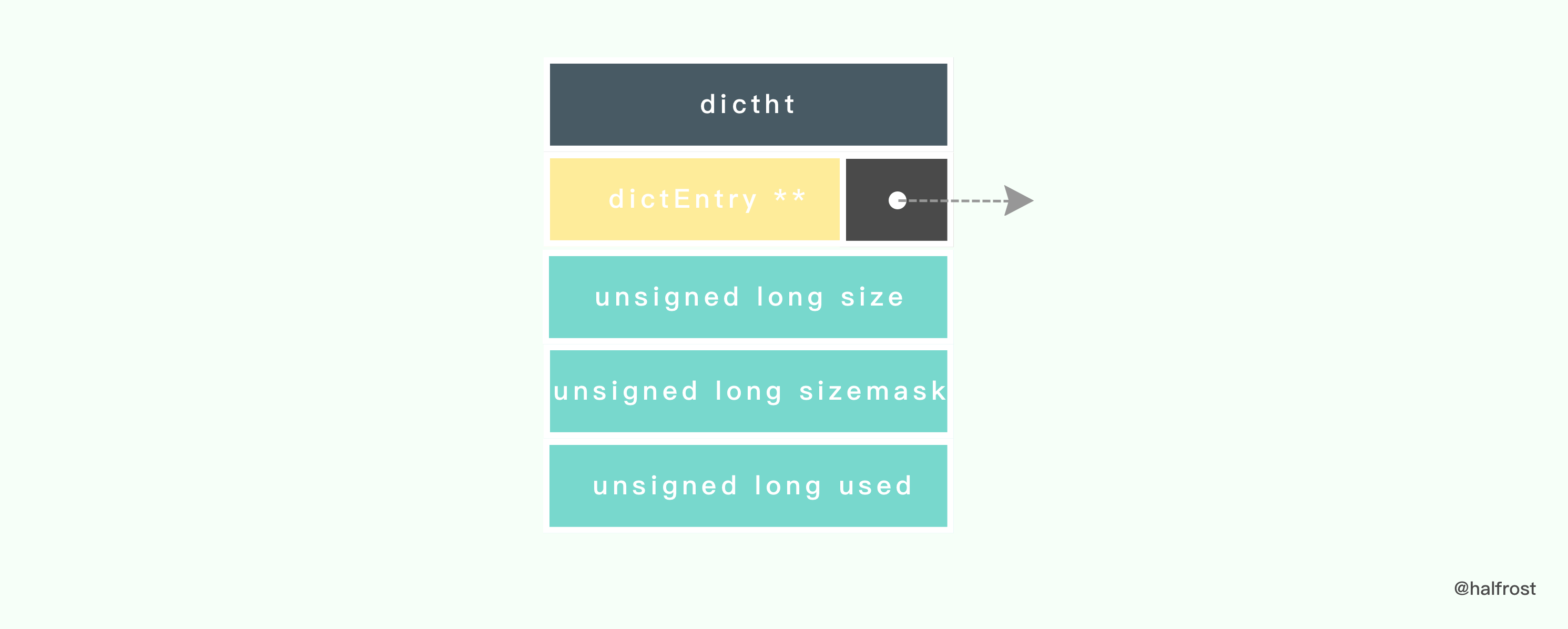
在 Redis 中定义了如下的哈希表的数据结构:
typedef struct dictht {dictEntry **table;unsigned long size;unsigned long sizemask;unsigned long used;} dictht;
table 属性是个数组, 数组的每个元素都是个指向 dictEntry 结构的指针。
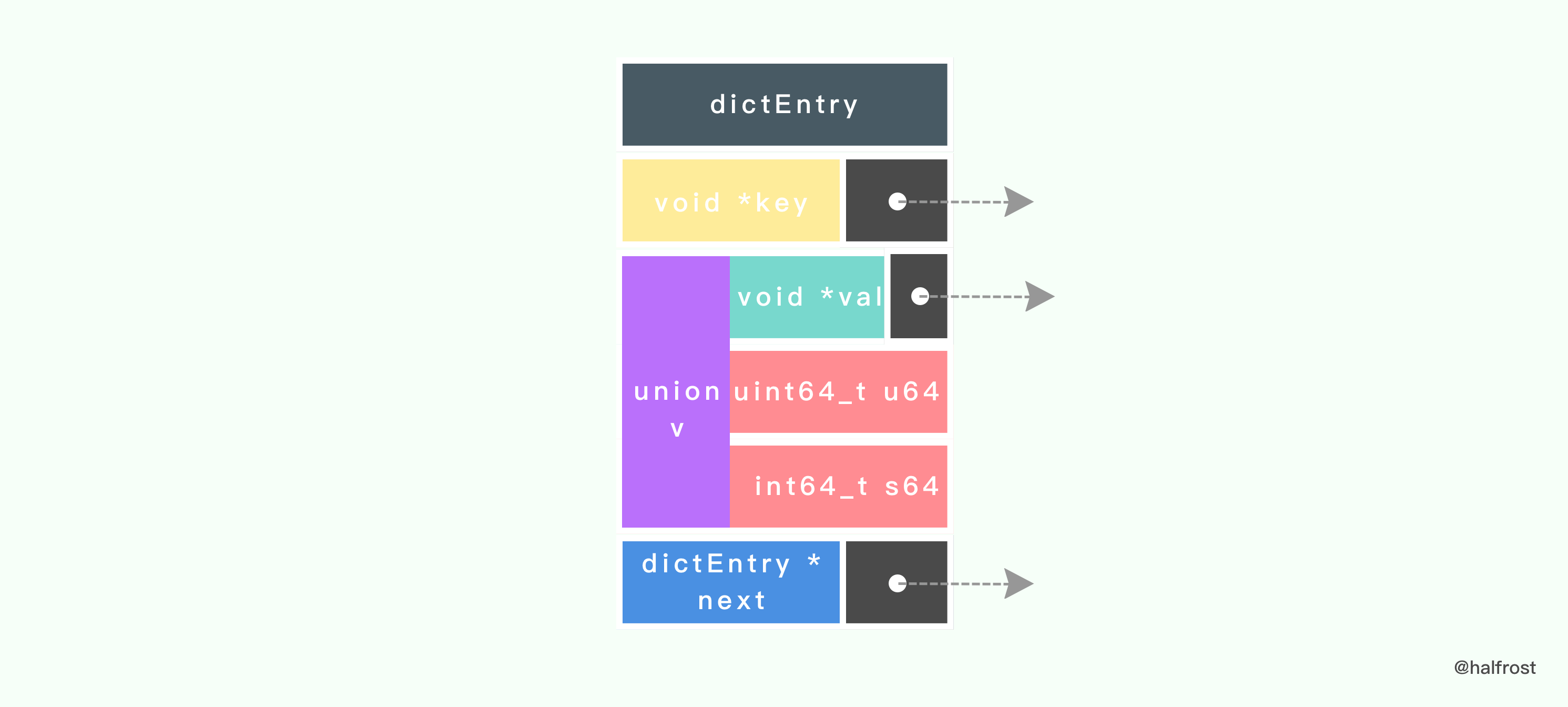
每个 dictEntry 都保存着一个键值对, 以及一个指向另一个 dictEntry 结构的指针:
typedef struct dictEntry {void *key;union {void *val;uint64_t u64;int64_t s64;} v;struct dictEntry *next;} dictEntry;
next 属性指向另一个 dictEntry 结构, 多个 dictEntry 可以通过 next 指针串连成链表, 从这里可以看出, dictht 使用链地址法来处理键碰撞问题的。
dictAdd 在每次向字典添加新键值对之前, 都会对哈希表 ht[0] 进行检查, 对于 ht[0] 的 size 和 used 属性, 如果它们之间的比率 ratio = used / size 满足以下任何一个条件的话,rehash 过程就会被激活:
自然 rehash : ratio >= 1 ,且变量 dict_can_resize 为真。
强制 rehash : ratio 大于变量 dict_force_resize_ratio (目前版本中, dict_force_resize_ratio 的值为 5 )。
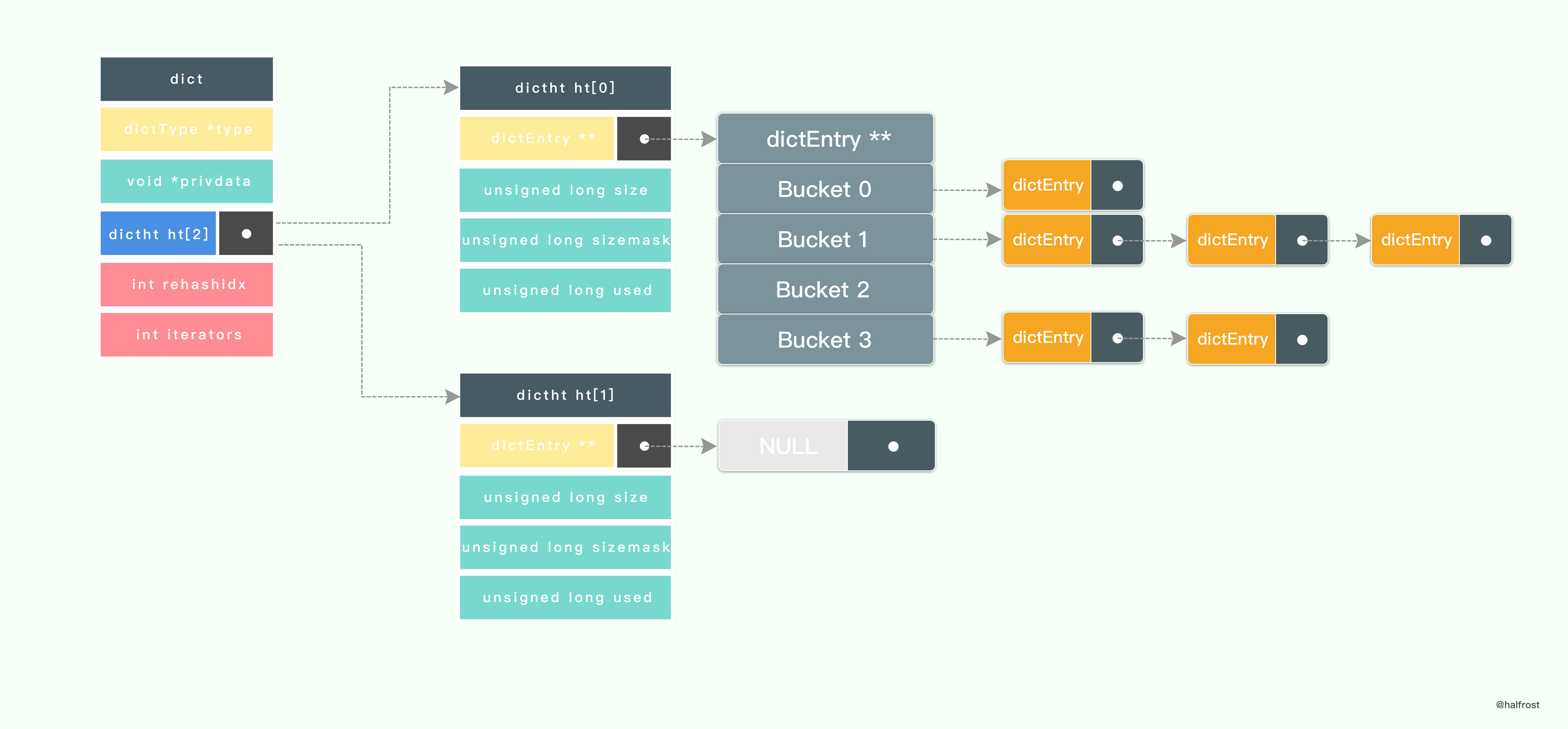
假设当前的字典需要扩容 rehash,那么 Redis 会先设置字典的 rehashidx 为 0 ,标识着 rehash 的开始;再为 ht[1]->table 分配空间,大小至少为 ht[0]->used 的两倍。
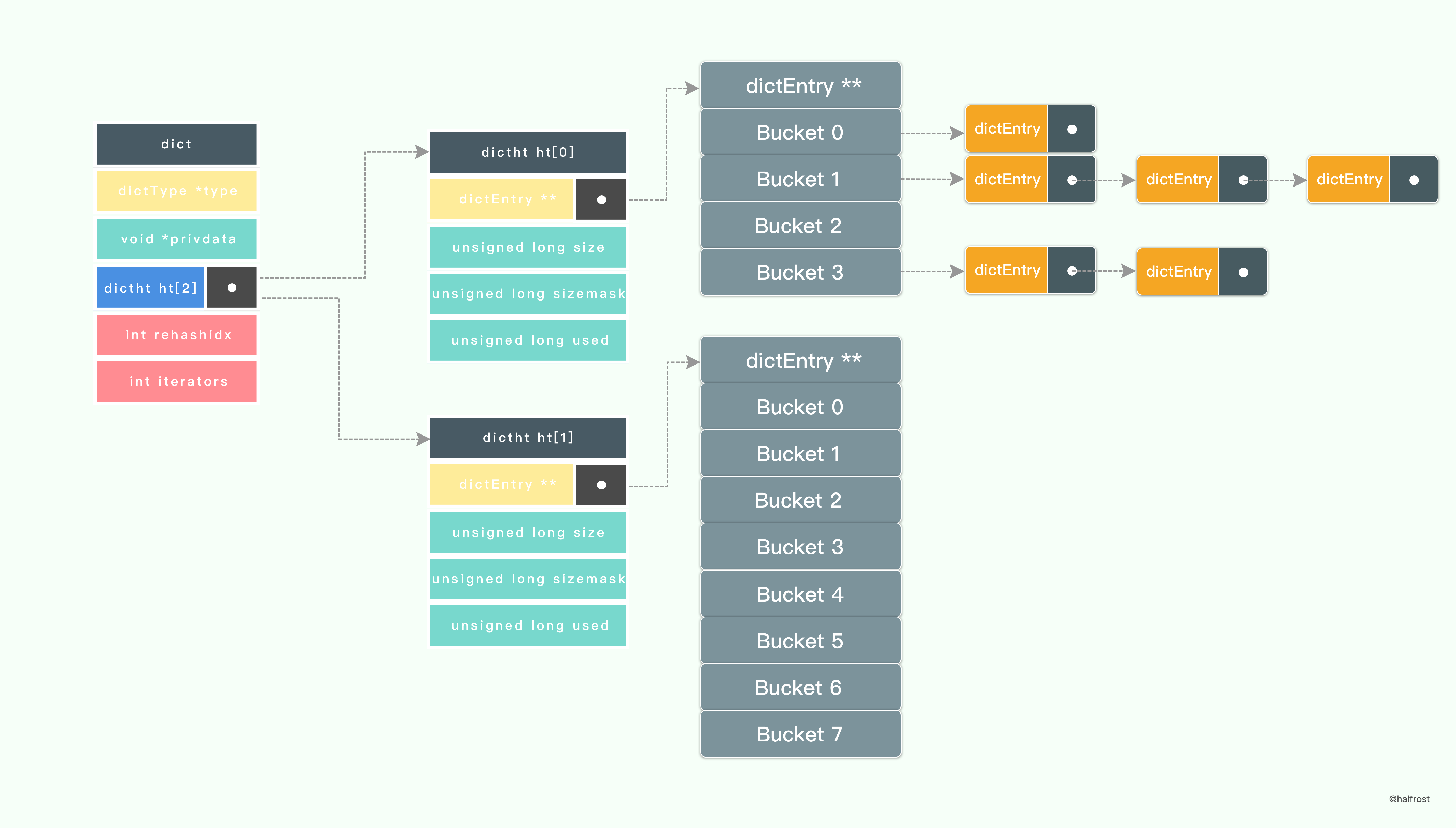
如上图, ht[1]->table 已经分配空间了 8 个空间了。
接着,开始 rehash 。将 ht[0]->table 内的键值移动到 ht[1]->table 中,键值的移动不是一次完成的,分多次进行。
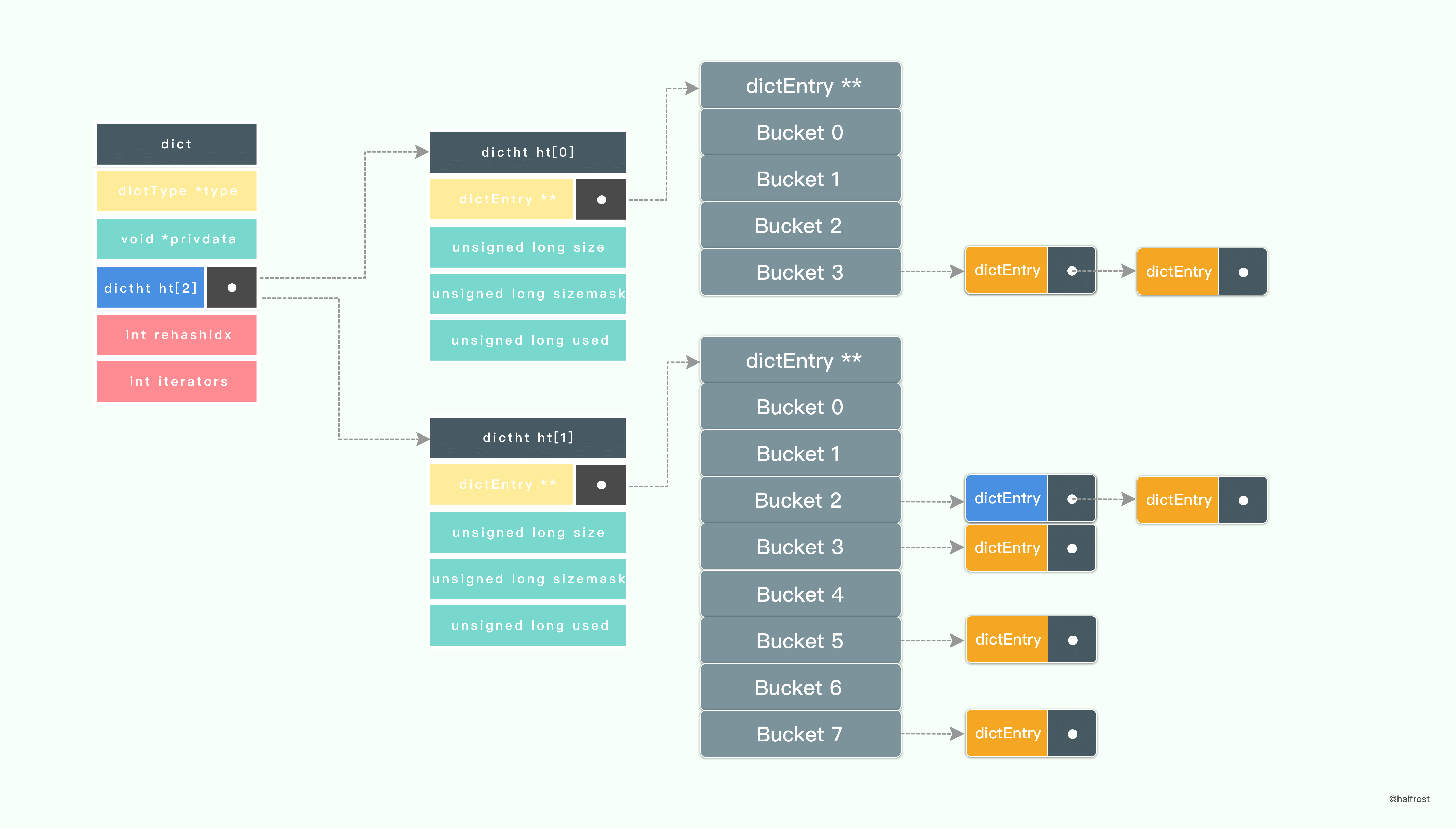
上图可以看出来, ht[0] 中的一部分键值已经迁移到 ht[1] 中了,并且此时还有新的键值插入进来,是直接插入到 ht[1] 中的,不会再插入到 ht[0] 中了。保证了 ht[0] 只减不增。
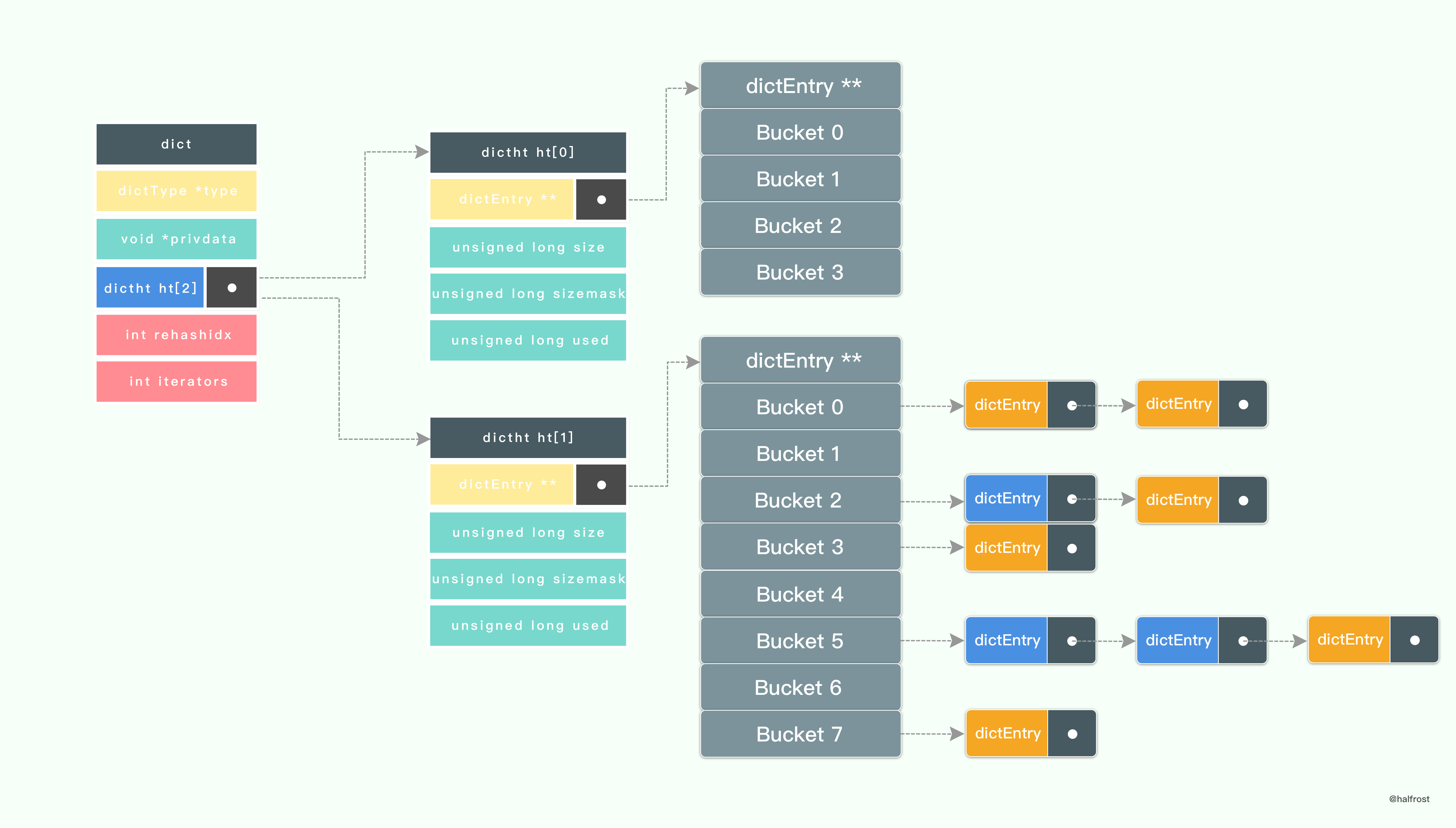
在 rehash 进行的过程中,不断的有新的键值插入进来,也不断的把 ht[0] 中的键值都迁移过来,直到 ht[0] 中的键值都迁移过来为止。注意 Redis 用的是头插法,新值永远都插在链表的第一个位置,这样也不用遍历到链表的最后,省去了 O(n) 的时间复杂度。进行到上图这种情况,所有的节点也就迁移完毕了。
rehash 在结束之前会进行清理工作,释放 ht[0] 的空间;用 ht[1] 来代替 ht[0] ,使原来的 ht[1] 成为新的 ht[0] ;创建一个新的空哈希表,并将它设置为 ht[1] ;将字典的 rehashidx 属性设置为 -1 ,标识 rehash 已停止;
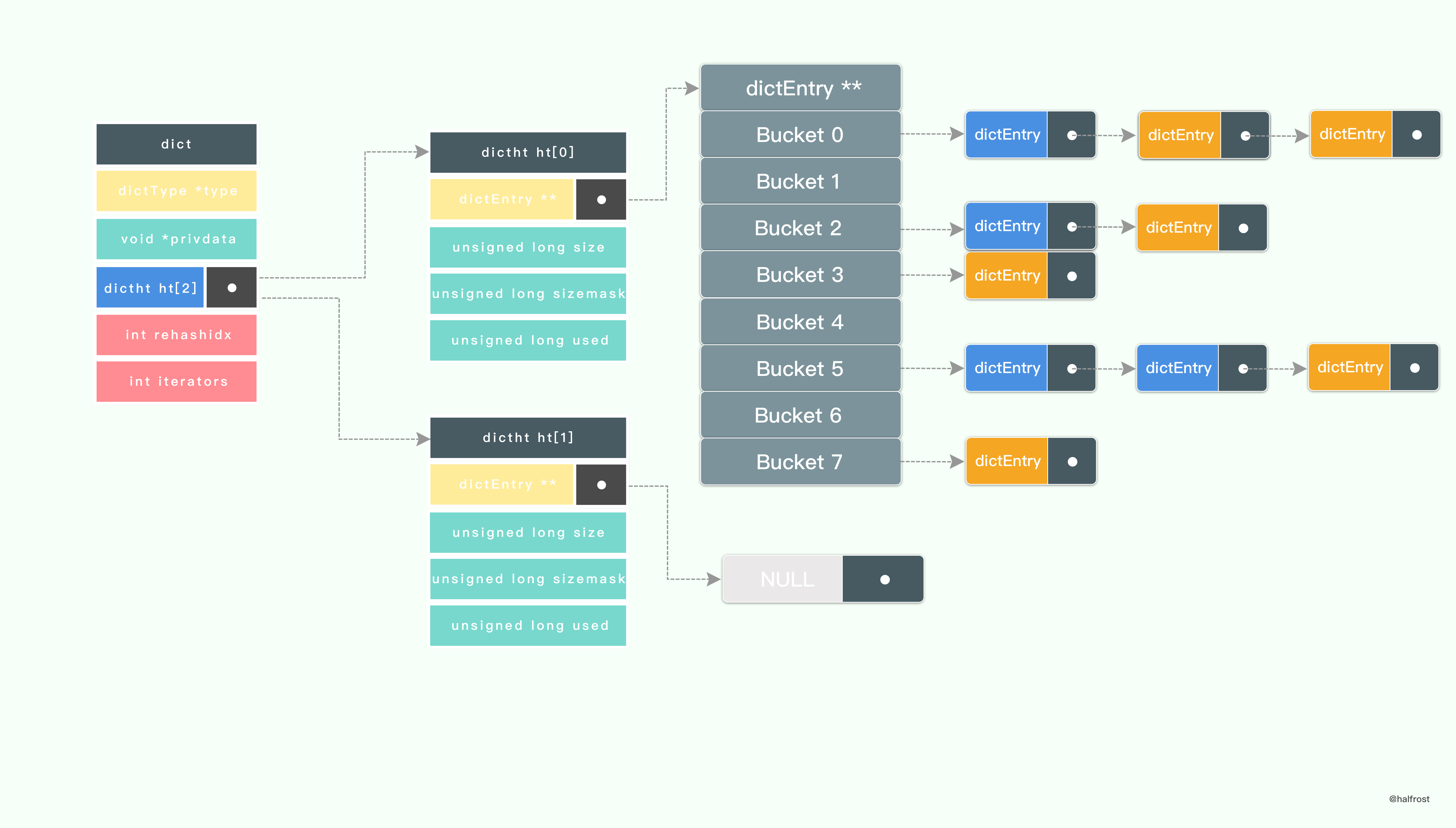
最终 rehash 结束以后情况如上图。如果还下次还需要 rehash ,重复上述过程即可。这种分多次,渐进式 rehash 的方式也成就了 Redis 的高性能。
值得一提的是,Redis 是支持字典的 reshrink 操作的。操作步骤就是
rehash 的逆过程。
二. 红黑树优化
读到这里,读者应该已经明白了到底用什么方式来控制 map 使得
Hash 碰撞的概率又小,哈希桶数组占用空间又少了吧,答案就是选择好的 Hash 算法和增加扩容机制。
Java 在 JDK1.8 对 HashMap 底层的实现再次进行了优化。
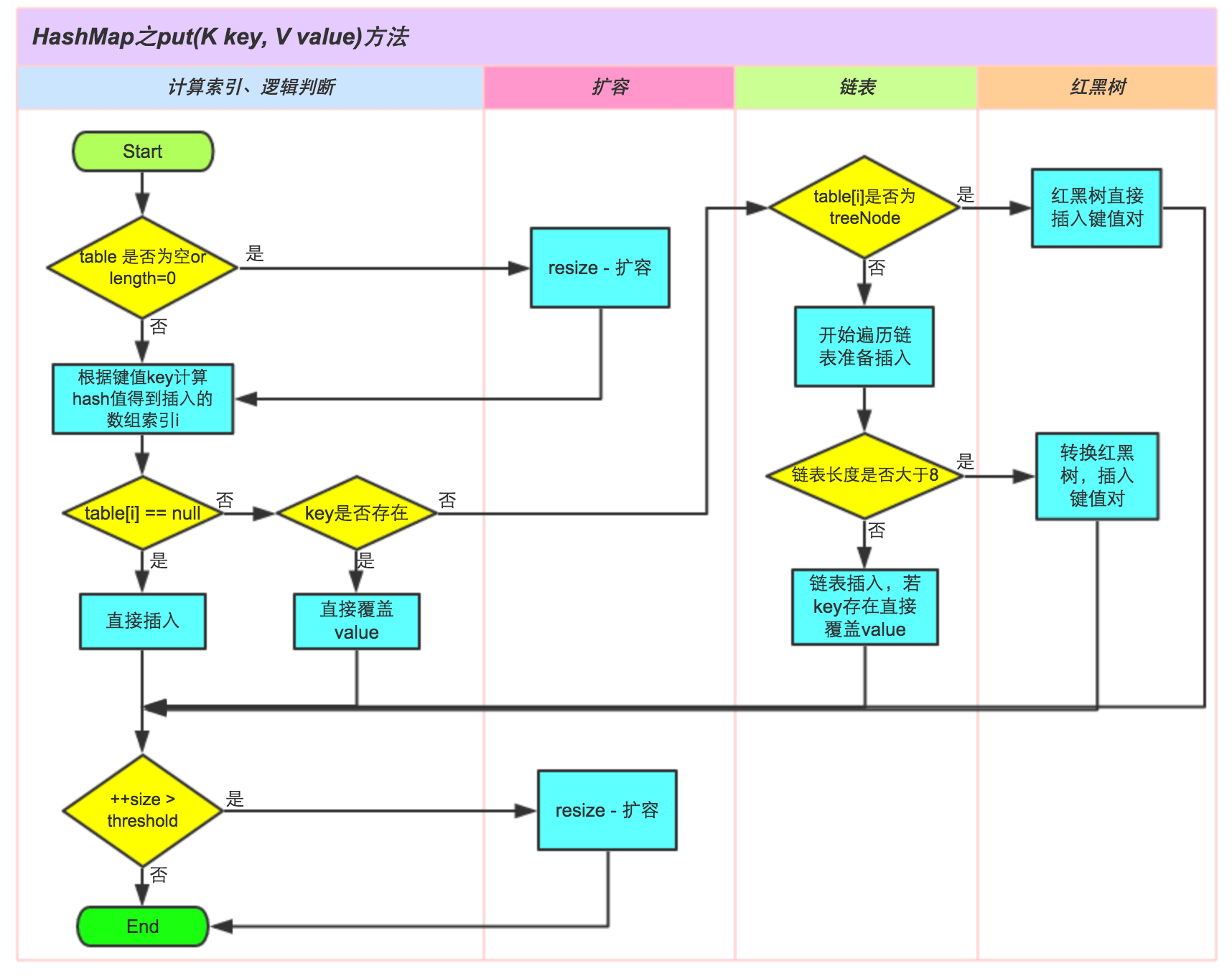
上图是来自美团博客总结的。从这里我们可以发现:
Java 底层初始桶的个数是 16 个,负载因子默认是 0.75,也就是说当键值第一次达到 12 个的时候就会进行扩容 resize。扩容的临界值在 64,当超过了 64 以后,并且冲突节点为 8 或者大于 8,这个时候就会触发红黑树转换。为了防止底层链表过长,链表就转换为红黑树。
换句话说,当桶的总个数没有到 64 个的时候,即使链表长为 8,也不会进行红黑树转换。
如果节点小于 6 个,红黑树又会重新退化成链表。
当然这里之所以选择用红黑树来进行优化,保证最坏情况不会退化成
O(n),红黑树能保证最坏时间复杂度也为 O(log n)。
在美团博客中也提到了,Java 在 JDK1.8 中还有一个值得学习的优化。Java 在 rehash 的键值节点迁移过程中,不需要再次计算一次 hash 计算!
由于使用了 2 次幂的扩展 (指长度扩为原来 2 倍),所以,元素的位置要么是在原位置,要么是在原位置再移动 2 次幂的位置。看下图可以明白这句话的意思,n 为 table 的长度,图(a)表示扩容前的 key1 和
key2 两种 key 确定索引位置的示例,图(b)表示扩容后 key1 和
key2 两种 key 确定索引位置的示例,其中 hash1 是 key1 对应的哈希与高位运算结果。
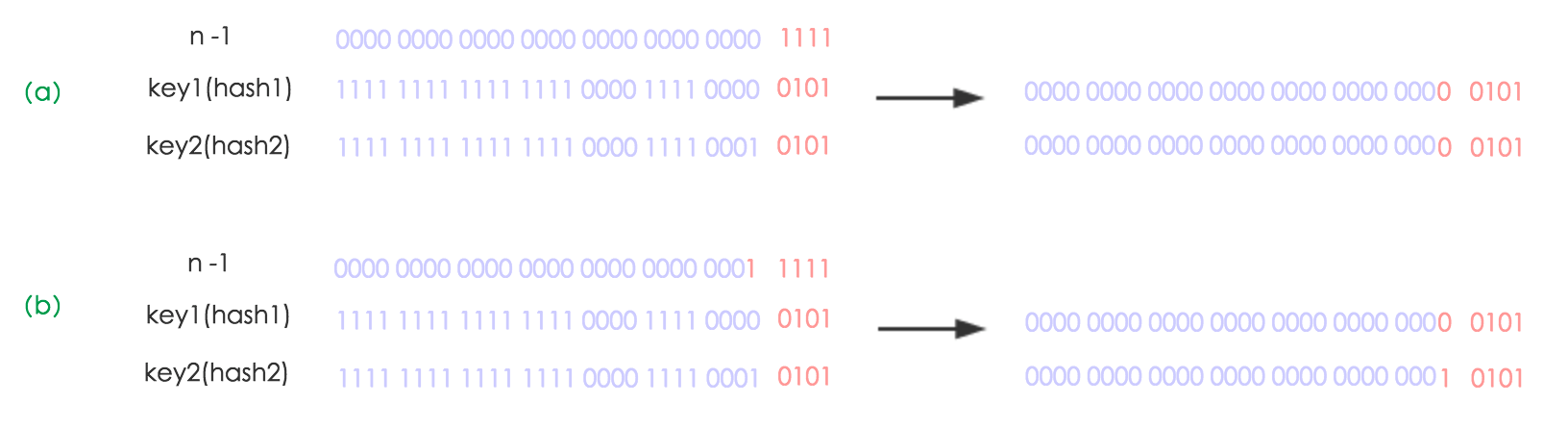
元素在重新计算 hash 之后,因为 n 变为 2 倍,那么 n-1 的 mask 范围在高位多 1bit(红色),因此新的 index 就会发生这样的变化:
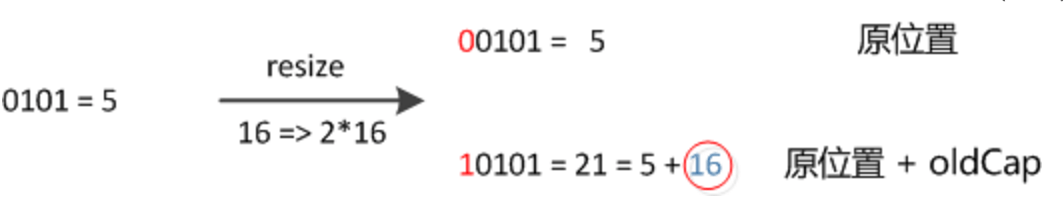
所以在扩容以后,就只需要看扩容容量以后那个位上的值为 0,还是为 1,如果是 0,代表索引不变,如果是 1,代表的是新的索引值等于原来的索引值加上 oldCap 即可,这样就不需要再次计算一次 hash 了。
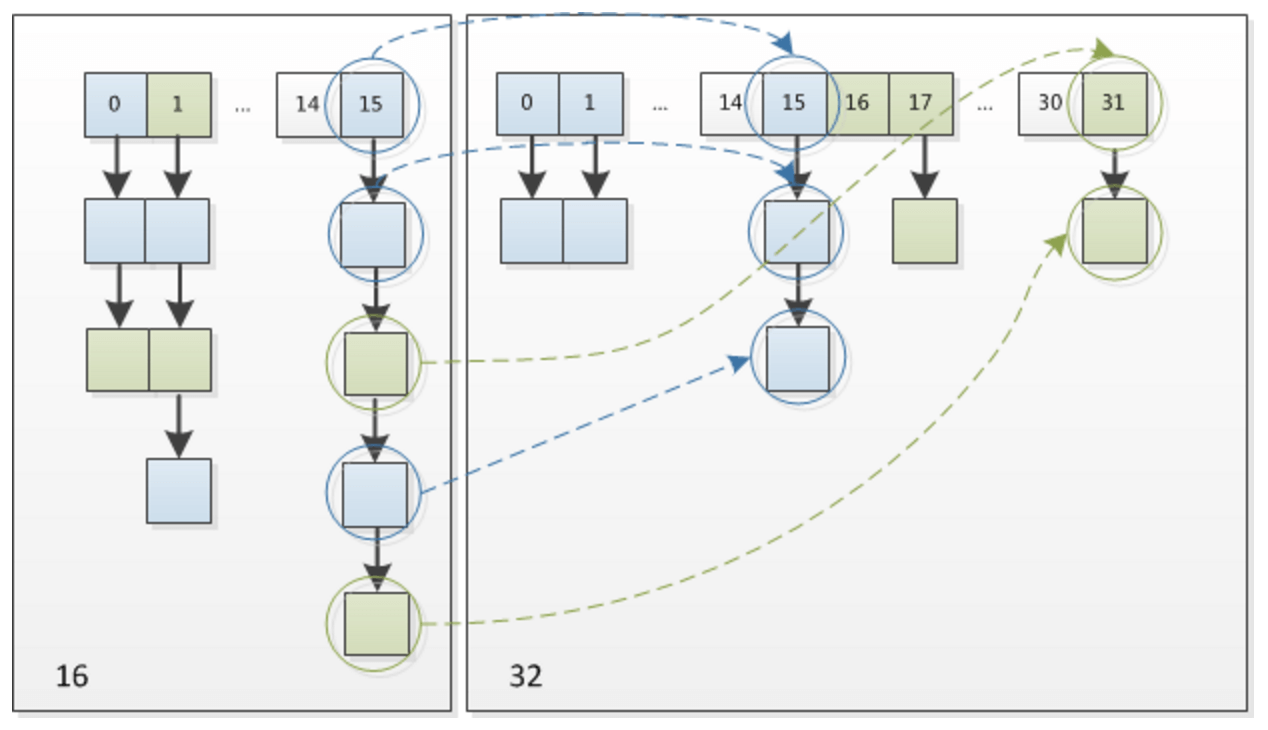
上图是把 16 扩容到 32 的情况。
三. Go 中 Map 的具体实现举例
读到这里,读者对如何设计一个 Map 应该有一些自己的想法了。选择一个优秀的哈希算法,用链表 + 数组 作为底层数据结构,如何扩容和优化,这些应该都有了解了。读到这里也许读者认为本篇文章内容已经过半了,不过前面这些都是偏理论,接下来也许才到了本文的重点部分 —— 从零开始分析一下完整的 Map 实现。
接下来笔者对 Go 中的 Map 的底层实现进行分析,也算是对一个 Map 的具体实现和重要的几个操作,添加键值,删除键值,扩容策略进行举例。
Go 的 map 实现在 /src/runtime/hashmap.go 这个文件中。
map 底层实质还是一个 hash table。
先来看看 Go 定义了一些常量。
const (bucketCntBits = 3bucketCnt = 1 << bucketCntBitsloadFactor = 6.5maxKeySize = 128maxValueSize = 128dataOffset = unsafe.Offsetof(struct {b bmapv int64}{}.v)empty = 0evacuatedEmpty = 1evacuatedX = 2evacuatedY = 3minTopHash = 4iterator = 1oldIterator = 2hashWriting = 4sameSizeGrow = 8noCheck = 1<<(8*sys.PtrSize) - 1)
这里值得说明的一点是触发扩容操作的临界值 6.5 是怎么得来的。这个值太大会导致 overflow buckets 过多,查找效率降低,过小会浪费存储空间。
据 Google 开发人员称,这个值是一个测试的程序,测量出来选择的一个经验值。
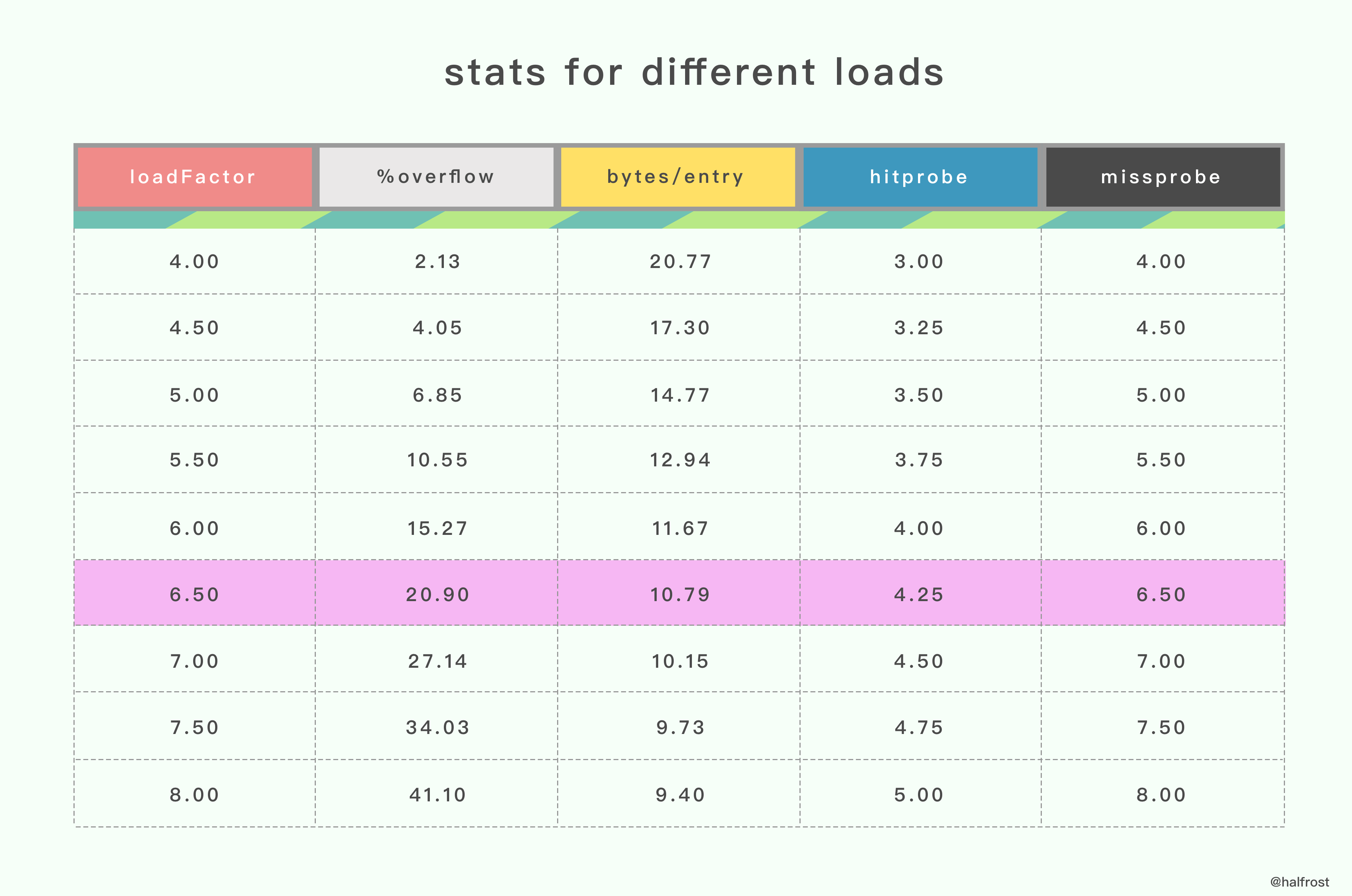
%overflow :
溢出率,平均一个 bucket 有多少个 键值 kv 的时候会溢出。
bytes/entry :
平均存一个 键值 kv 需要额外存储多少字节的数据。
hitprobe :
查找一个存在的 key 平均查找次数。
missprobe :
查找一个不存在的 key 平均查找次数。
经过这几组测试数据,最终选定 6.5 作为临界的装载因子。
接着看看 Go 中 map header 的定义:
type hmap struct {count intflags uint8B uint8noverflow uint16hash0 uint32buckets unsafe.Pointeroldbuckets unsafe.Pointernevacuate uintptrextra *mapextra}
在 Go 的 map header 结构中,也包含了 2 个指向桶数组的指针,buckets 指向新的桶数组,oldbuckets 指向旧的桶数组。这点和 Redis 字典中也有两个 dictht 数组类似。
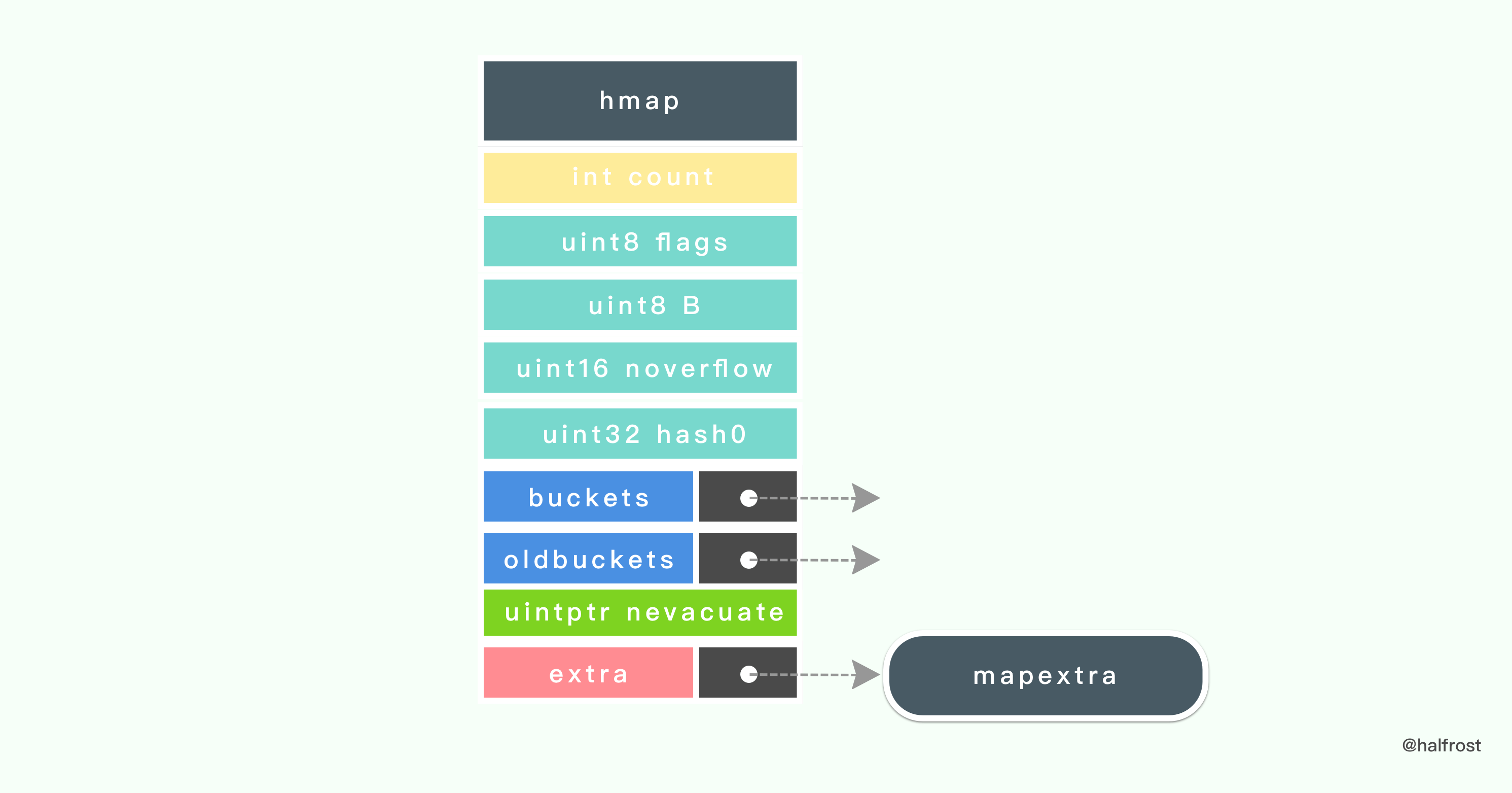
hmap 的最后一个字段是一个指向 mapextra 结构的指针,它的定义如下:
type mapextra struct {overflow [2]*[]*bmapnextOverflow *bmap}
如果一个键值对没有找到对应的指针,那么就会把它们先存到溢出桶
overflow 里面。在 mapextra 中还有一个指向下一个可用的溢出桶的指针。
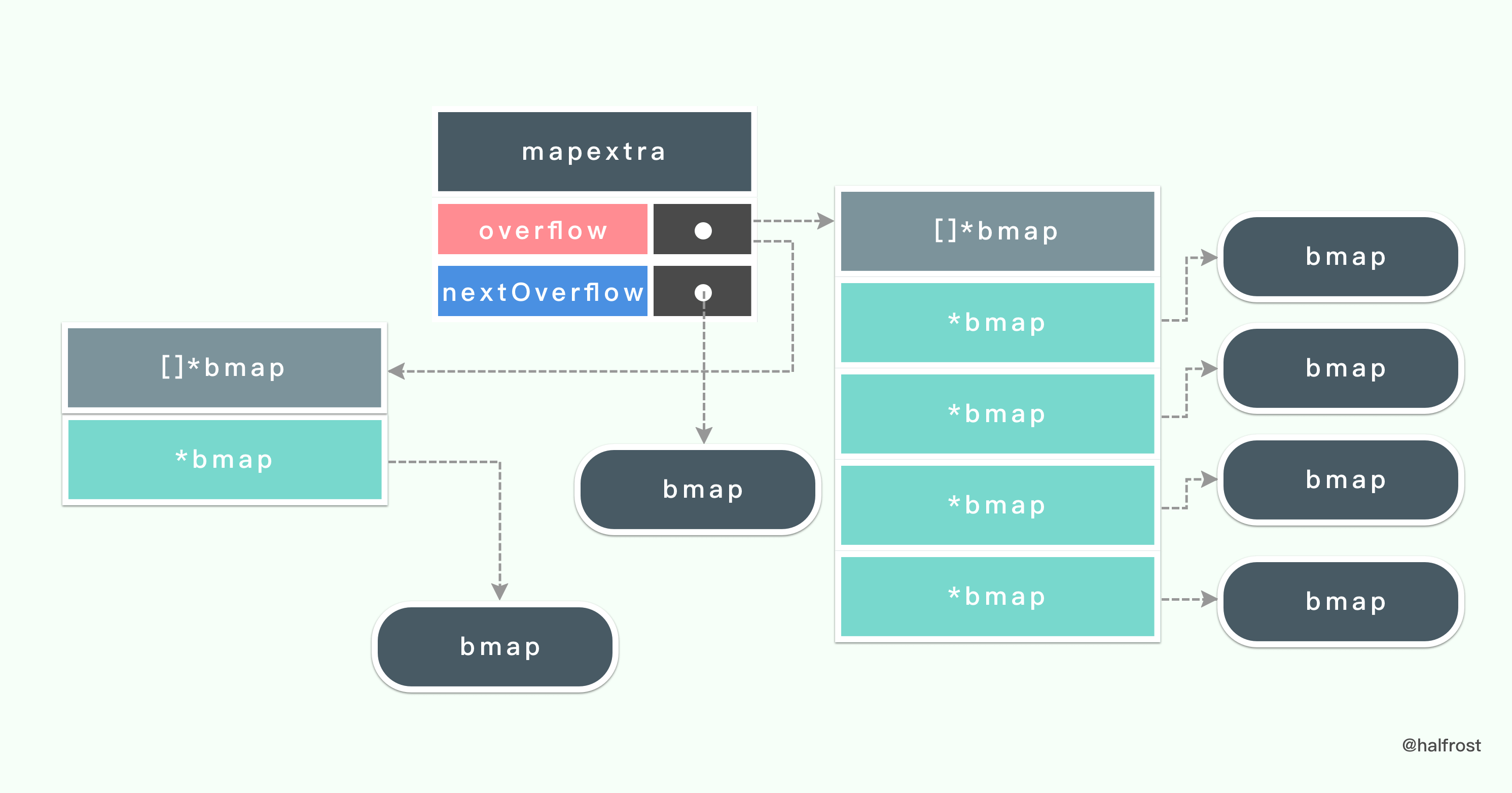
溢出桶 overflow 是一个数组,里面存了 2 个指向 *bmap 数组的指针。overflow[0] 里面装的是 hmap.buckets 。overflow[1] 里面装的是 hmap.oldbuckets。
再看看桶的数据结构的定义,bmap 就是 Go 中 map 里面桶对应的结构体类型。
type bmap struct {tophash [bucketCnt]uint8}
桶的定义比较简单,里面就只是包含了一个 uint8 类型的数组,里面包含 8 个元素。这 8 个元素存储的是 hash 值的高 8 位。
在 tophash 之后的内存布局里还有 2 块内容。紧接着 tophash 之后的是 8 对 键值 key- value 对。并且排列方式是 8 个 key 和 8 个 value 放在一起。
8 对 键值 key- value 对结束以后紧接着一个 overflow 指针,指向下一个 bmap。从此也可以看出 Go 中 map 是用链表的方式处理 hash 冲突的。
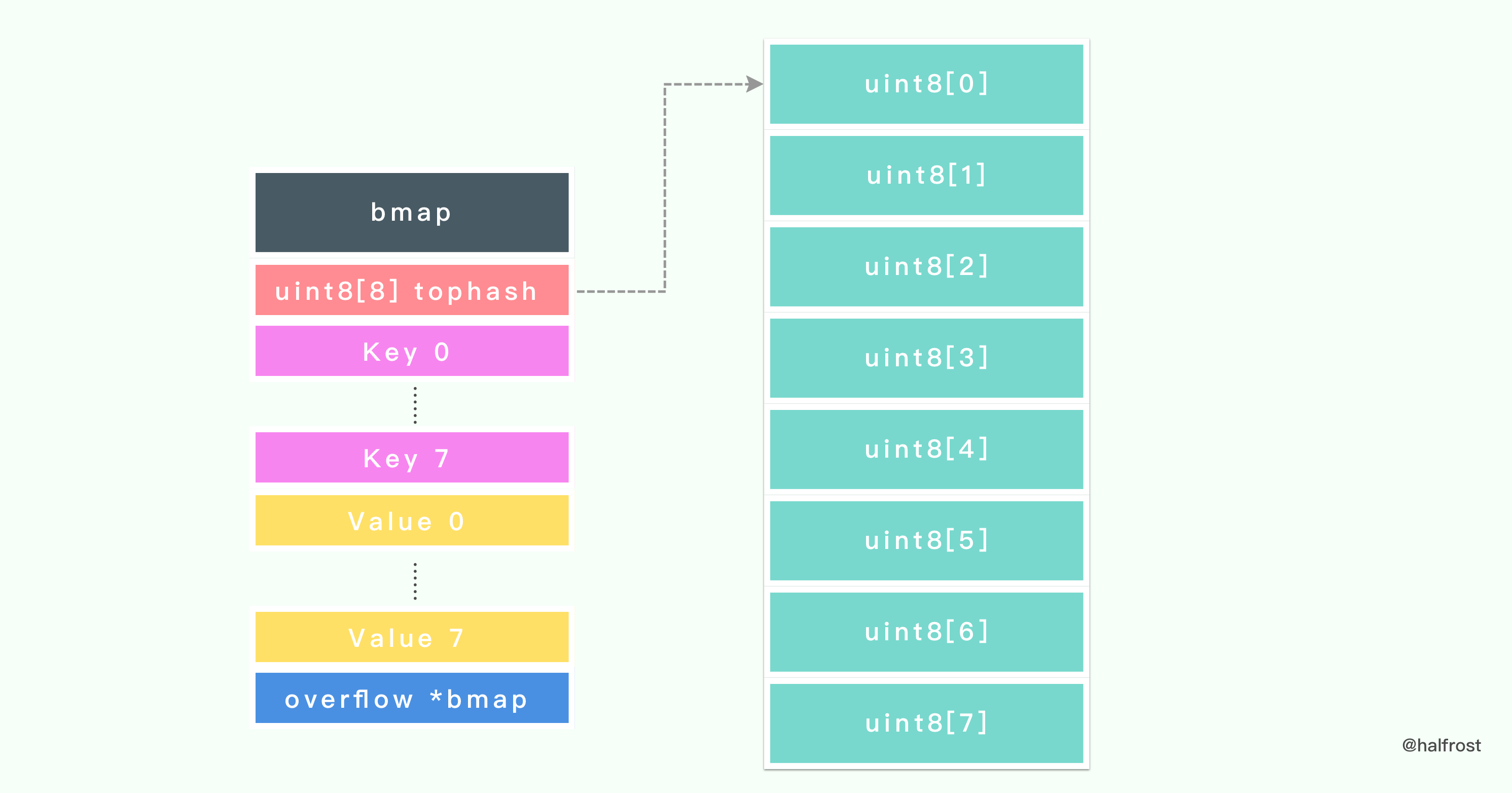
为何 Go 存储键值对的方式不是普通的 key/value、key/value、key/value…… 这样存储的呢?它是键 key 都存储在一起,然后紧接着是 值 value 都存储在一起,为什么会这样呢?

在 Redis 中,当使用 REDIS_ENCODING_ZIPLIST 编码哈希表时, 程序通过将键和值一同推入压缩列表, 从而形成保存哈希表所需的键 - 值对结构,如上图。新添加的 key-value 对会被添加到压缩列表的表尾。
这种结构有一个弊端,如果存储的键和值的类型不同,在内存中布局中所占字节不同的话,就需要对齐。比如说存储一个 map[int64]int8 类型的字典。
Go 为了节约内存对齐的内存消耗,于是把它设计成上图所示那样。
如果 map 里面存储了上万亿的大数据,这里节约出来的内存空间还是比较可观的。
1. 新建 Map
makemap 新建了一个 Map,如果入参 h 不为空,那么 map 的 hmap 就是入参的这个 hmap,如果入参 bucket 不为空,那么这个 bucket 桶就作为第一个桶。
func makemap(t *maptype, hint int64, h *hmap, bucket unsafe.Pointer) *hmap {if sz := unsafe.Sizeof(hmap{}); sz > 48 || sz != t.hmap.size {println("runtime: sizeof(hmap) =", sz, ", t.hmap.size =", t.hmap.size)throw("bad hmap size")}if hint < 0 || hint > int64(maxSliceCap(t.bucket.size)) {hint = 0}if !ismapkey(t.key) {throw("runtime.makemap: unsupported map key type")}if t.key.size > maxKeySize && (!t.indirectkey || t.keysize != uint8(sys.PtrSize)) ||t.key.size <= maxKeySize && (t.indirectkey || t.keysize != uint8(t.key.size)) {throw("key size wrong")}if t.elem.size > maxValueSize && (!t.indirectvalue || t.valuesize != uint8(sys.PtrSize)) ||t.elem.size <= maxValueSize && (t.indirectvalue || t.valuesize != uint8(t.elem.size)) {throw("value size wrong")}if t.key.align > bucketCnt {throw("key align too big")}if t.elem.align > bucketCnt {throw("value align too big")}if t.key.size%uintptr(t.key.align) != 0 {throw("key size not a multiple of key align")}if t.elem.size%uintptr(t.elem.align) != 0 {throw("value size not a multiple of value align")}if bucketCnt < 8 {throw("bucketsize too small for proper alignment")}if dataOffset%uintptr(t.key.align) != 0 {throw("need padding in bucket (key)")}if dataOffset%uintptr(t.elem.align) != 0 {throw("need padding in bucket (value)")}B := uint8(0)for ; overLoadFactor(hint, B); B++ {}buckets := bucketvar extra *mapextraif B != 0 {var nextOverflow *bmapbuckets, nextOverflow = makeBucketArray(t, B)if nextOverflow != nil {extra = new(mapextra)extra.nextOverflow = nextOverflow}}if h == nil {h = (*hmap)(newobject(t.hmap))}h.count = 0h.B = Bh.extra = extrah.flags = 0h.hash0 = fastrand()h.buckets = bucketsh.oldbuckets = nilh.nevacuate = 0h.noverflow = 0return h}
新建一个 map 最重要的就是分配内存并初始化哈希表,在 B 不为 0 的情况下,还会初始化 mapextra 并且会 buckets 会被重新生成。
func makeBucketArray(t *maptype, b uint8) (buckets unsafe.Pointer, nextOverflow *bmap) {base := uintptr(1 << b)nbuckets := baseif b >= 4 {nbuckets += 1 << (b - 4)sz := t.bucket.size * nbucketsup := roundupsize(sz)if up != sz {nbuckets = up / t.bucket.size}}buckets = newarray(t.bucket, int(nbuckets))if base != nbuckets {nextOverflow = (*bmap)(add(buckets, base*uintptr(t.bucketsize)))last := (*bmap)(add(buckets, (nbuckets-1)*uintptr(t.bucketsize)))last.setoverflow(t, (*bmap)(buckets))}return buckets, nextOverflow}
这里的 newarray 就已经是 mallocgc 了。
从上述代码里面可以看出,只有当 B >=4 的时候,makeBucketArray 才会生成 nextOverflow 指针指向 bmap,从而在 Map 生成 hmap 的时候才会生成 mapextra 。
当 B = 3 (B < 4) 的时候,初始化 hmap 只会生成 8 个桶。
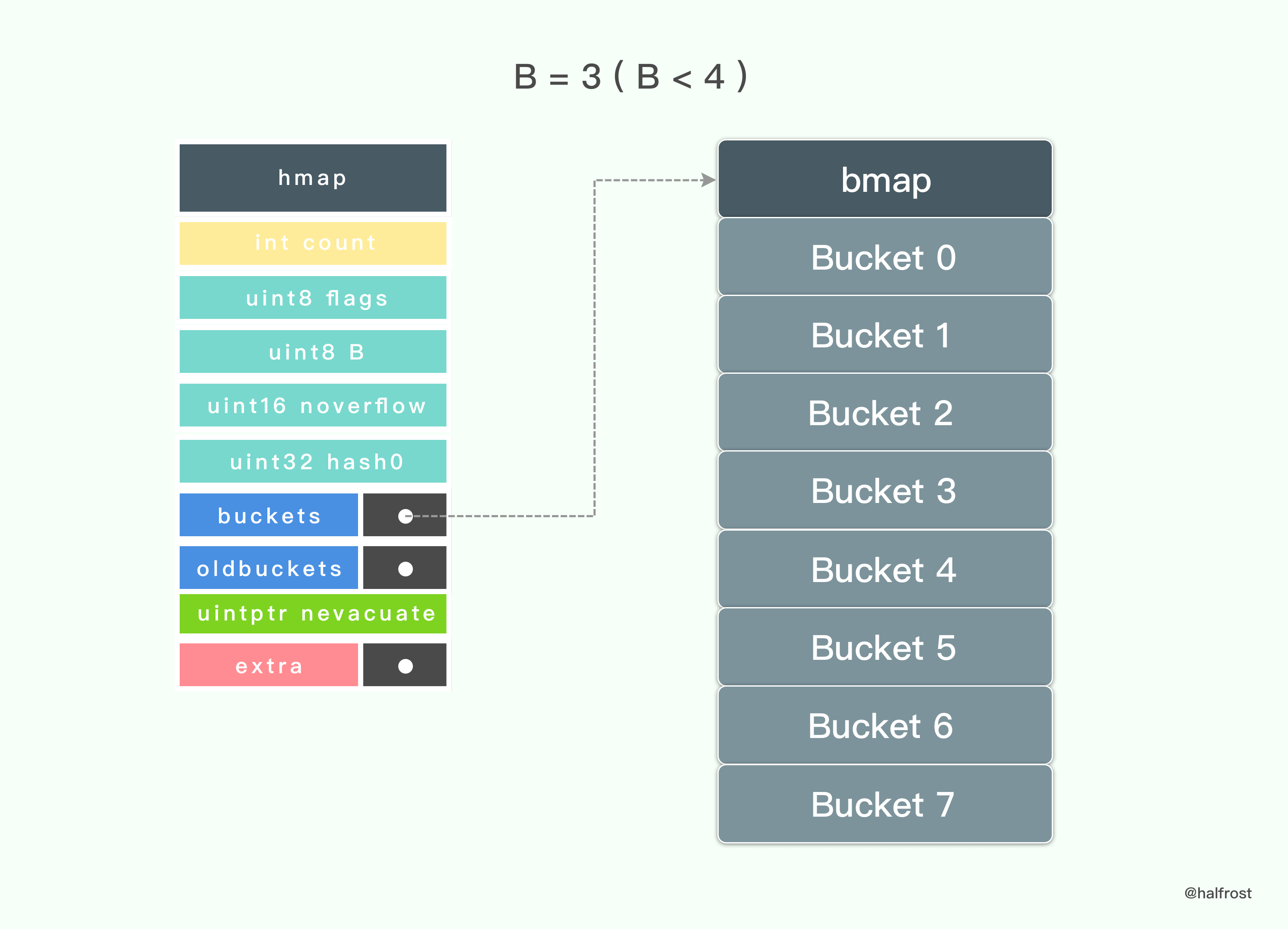
当 B = 4 (B>= 4 ) 的时候,初始化 hmap 的时候还会额外生成 mapextra ,并初始化 nextOverflow。mapextra 的 nextOverflow 指针会指向第 16 个桶结束,第 17 个桶的首地址。第 17 个桶(从 0 开始,也就是下标为 16 的桶)的 bucketsize - sys.PtrSize 地址开始存一个指针,这个指针指向当前整个桶的首地址。这个指针就是 bmap 的 overflow 指针。
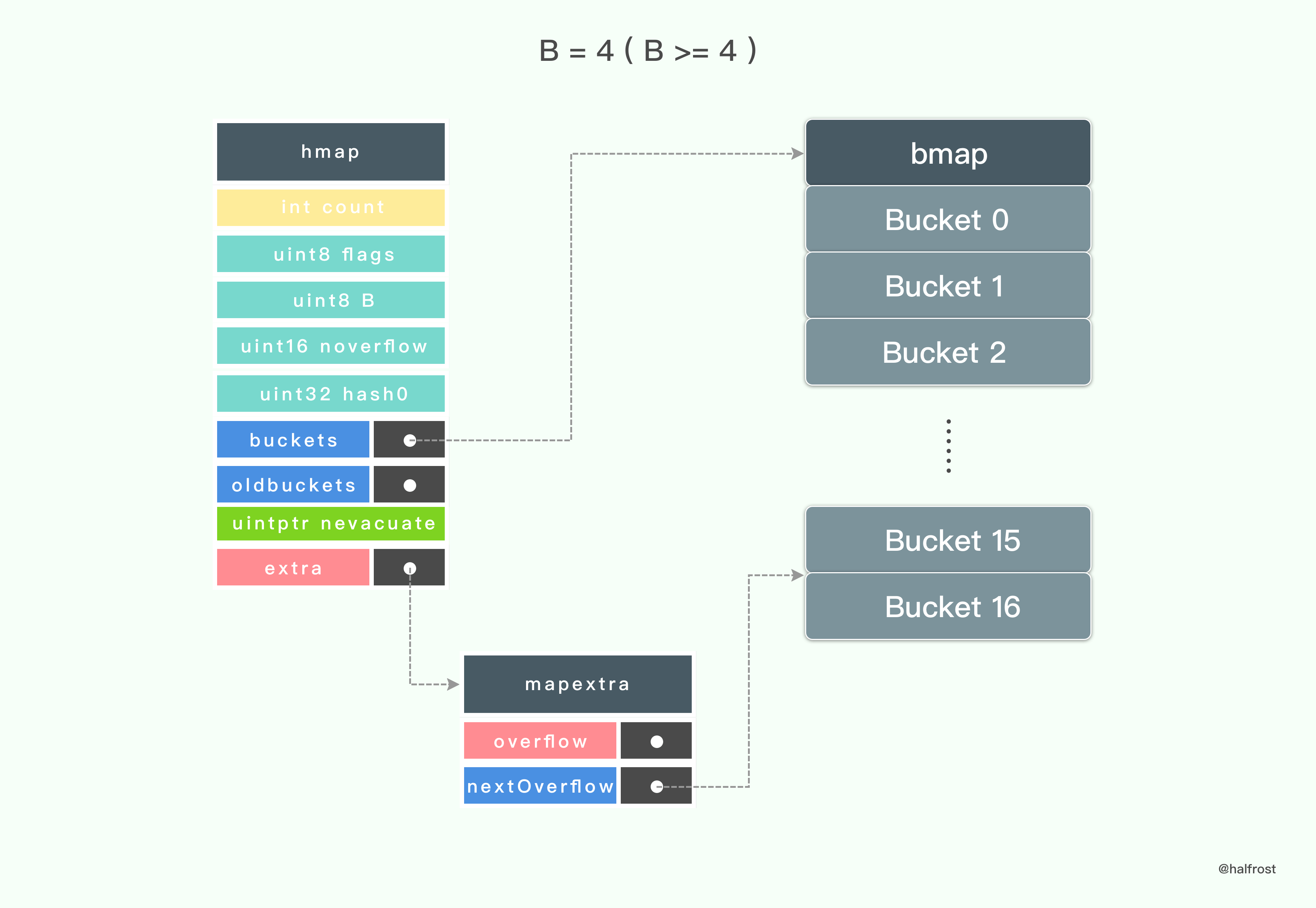
当 B = 5 (B>= 4 ) 的时候,初始化 hmap 的时候还会额外生成 mapextra ,并初始化 nextOverflow。这个时候就会生成总共 34 个桶了。同理,最后一个桶大小减去一个指针的大小的地址开始存储一个 overflow 指针。
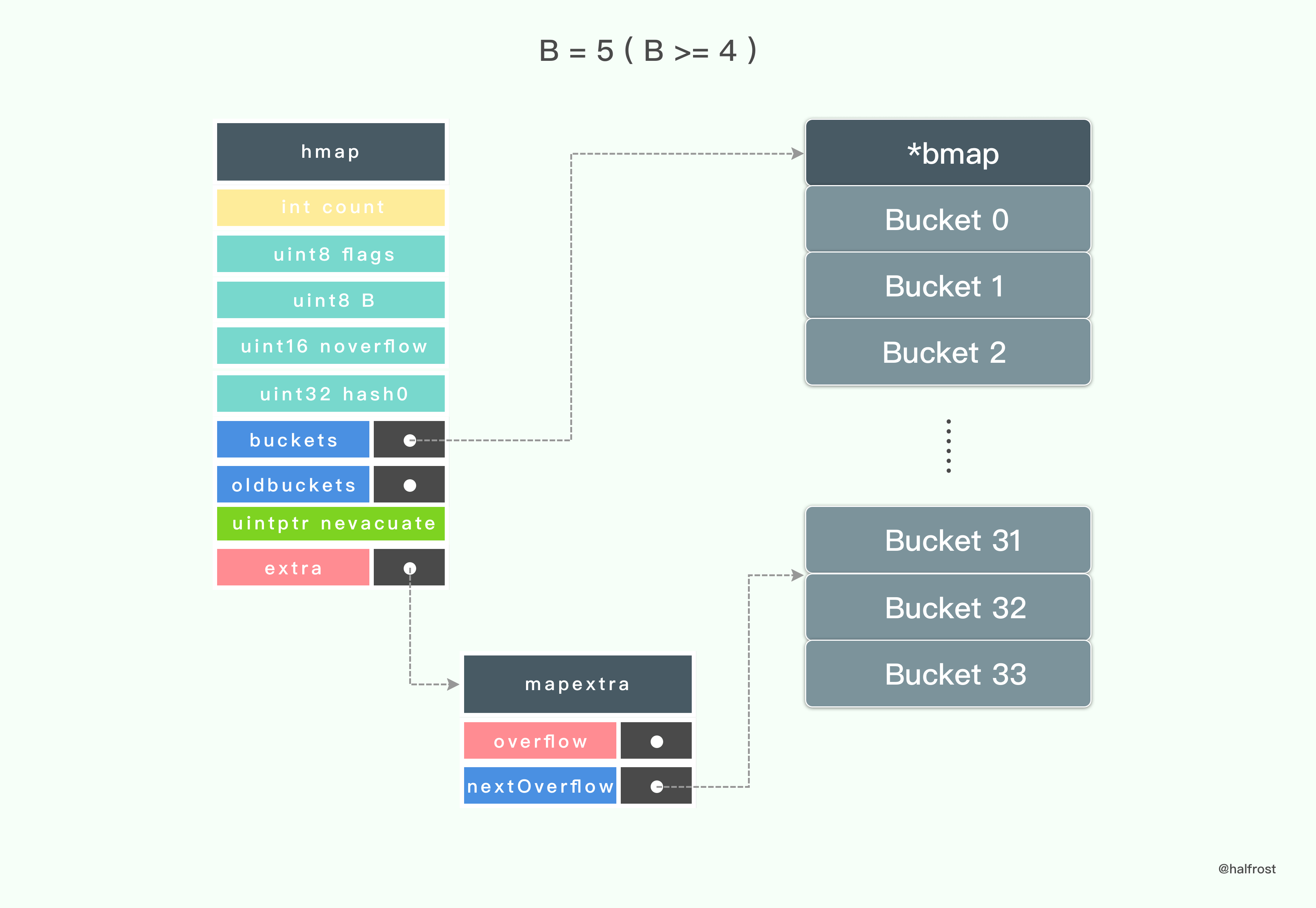
2. 查找 Key
在 Go 中,如果字典里面查找一个不存在的 key ,查找不到并不会返回一个 nil ,而是返回当前类型的零值。比如,字符串就返回空字符串,int 类型就返回 0 。
func mapaccess1(t *maptype, h *hmap, key unsafe.Pointer) unsafe.Pointer {if raceenabled && h != nil {callerpc := getcallerpc(unsafe.Pointer(&t))pc := funcPC(mapaccess1)racereadpc(unsafe.Pointer(h), callerpc, pc)raceReadObjectPC(t.key, key, callerpc, pc)}if msanenabled && h != nil {msanread(key, t.key.size)}if h == nil || h.count == 0 {return unsafe.Pointer(&zeroVal[0])}if h.flags&hashWriting != 0 {throw("concurrent map read and map write")}alg := t.key.alghash := alg.hash(key, uintptr(h.hash0))m := uintptr(1)<<h.B - 1b := (*bmap)(add(h.buckets, (hash&m)*uintptr(t.bucketsize)))if c := h.oldbuckets; c != nil {if !h.sameSizeGrow() {m >>= 1}oldb := (*bmap)(add(c, (hash&m)*uintptr(t.bucketsize)))if !evacuated(oldb) {b = oldb}}top := uint8(hash >> (sys.PtrSize*8 - 8))if top < minTopHash {top += minTopHash}for {for i := uintptr(0); i < bucketCnt; i++ {if b.tophash[i] != top {continue}k := add(unsafe.Pointer(b), dataOffset+i*uintptr(t.keysize))if t.indirectkey {k = *((*unsafe.Pointer)(k))}if alg.equal(key, k) {v := add(unsafe.Pointer(b), dataOffset+bucketCnt*uintptr(t.keysize)+i*uintptr(t.valuesize))if t.indirectvalue {v = *((*unsafe.Pointer)(v))}return v}}b = b.overflow(t)if b == nil {return unsafe.Pointer(&zeroVal[0])}}}
具体实现代码如上,详细解释见代码。
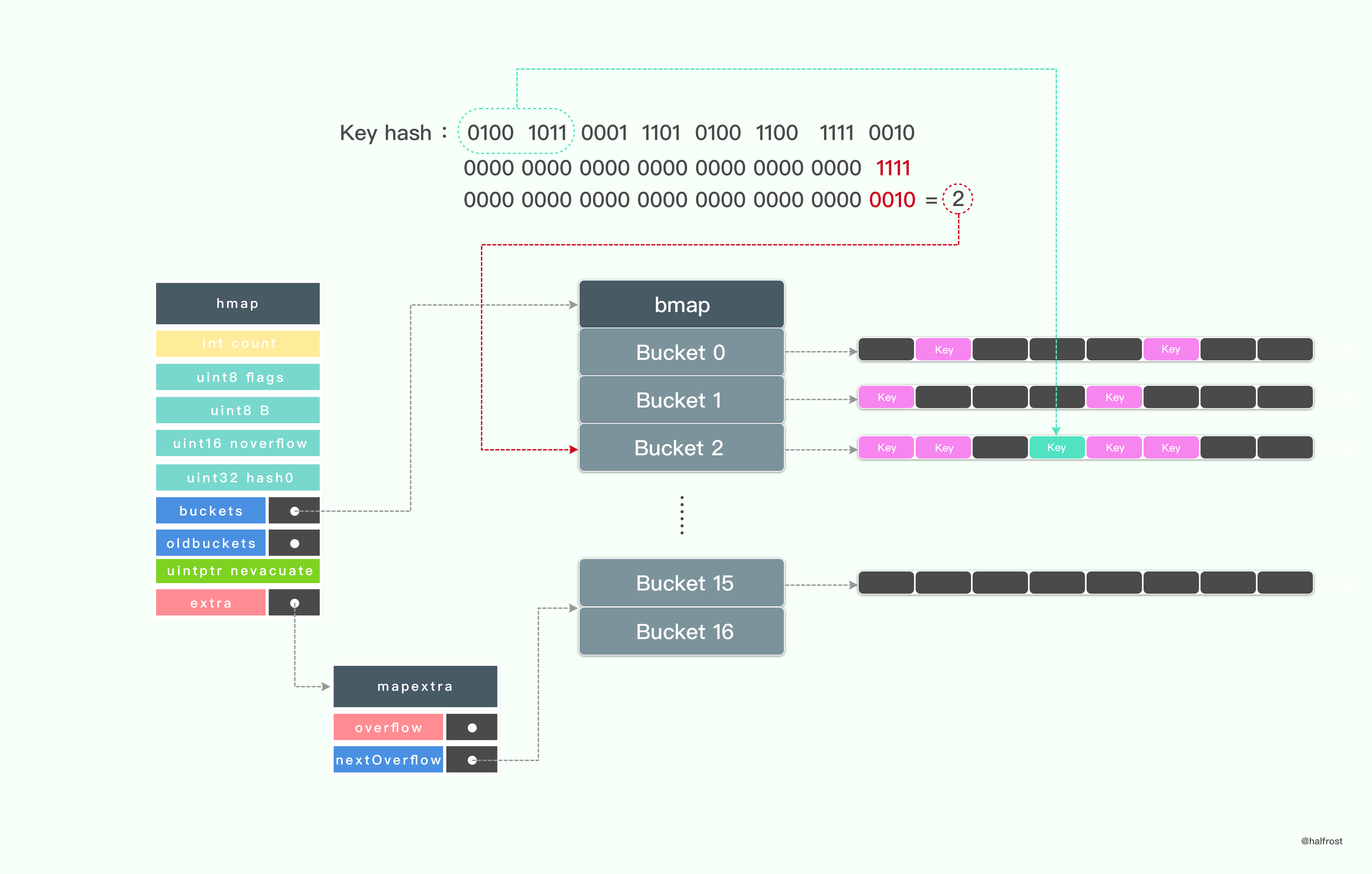
如上图,这是一个查找 key 的全过程。
首先计算出 key 对应的 hash 值,hash 值对 B 取余。
这里有一个优化点。m % n 这步计算,如果 n 是 2 的倍数,那么可以省去这一步取余操作。
m % n = m & ( n - 1 )
这样优化就可以省去耗时的取余操作了。这里例子中计算完取出来是 0010 ,也就是 2,于是对应的是桶数组里面的第 3 个桶。为什么是第 3 个桶呢?首地址指向第 0 个桶,往下偏移 2 个桶的大小,于是偏移到了第 3 个桶的首地址了,具体实现可以看上述代码。
hash 的低 B 位决定了桶数组里面的第几个桶,hash 值的高 8 位决定了这个桶数组 bmap 里面 key 存在 tophash 数组的第几位了。如上图,hash 的高 8 位用来和 tophash 数组里面的每个值进行对比,如果高 8 位和 tophash[i] 不等,就直接比下一个。如果相等,则取出 bmap 里面对应完整的 key,再比较一次,看是否完全一致。
整个查找过程优先在 oldbucket 里面找 (如果存在 lodbucket 的话),找完再去新 bmap 里面找。
有人可能会有疑问,为何这里要加入 tophash 多一次比较呢?
tophash 的引入是为了加速查找的。由于它只存了 hash 值的高 8 位,比查找完整的 64 位要快很多。通过比较高 8 位,迅速找到高 8 位一致 hash 值的索引,接下来再进行一次完整的比较,如果还一致,那么就判定找到该 key 了。
如果找到了 key 就返回对应的 value。如果没有找到,还会继续去 overflow 桶继续寻找,直到找到最后一个桶,如果还没有找到就返回对应类型的零值。
3. 插入 Key
插入 key 的过程和查找 key 的过程大体一致。
func mapassign(t *maptype, h *hmap, key unsafe.Pointer) unsafe.Pointer {if h == nil {panic(plainError("assignment to entry in nil map"))}if raceenabled {callerpc := getcallerpc(unsafe.Pointer(&t))pc := funcPC(mapassign)racewritepc(unsafe.Pointer(h), callerpc, pc)raceReadObjectPC(t.key, key, callerpc, pc)}if msanenabled {msanread(key, t.key.size)}if h.flags&hashWriting != 0 {throw("concurrent map writes")}alg := t.key.alghash := alg.hash(key, uintptr(h.hash0))h.flags |= hashWritingif h.buckets == nil {h.buckets = newarray(t.bucket, 1)}again:bucket := hash & (uintptr(1)<<h.B - 1)if h.growing() {growWork(t, h, bucket)}b := (*bmap)(unsafe.Pointer(uintptr(h.buckets) + bucket*uintptr(t.bucketsize)))top := uint8(hash >> (sys.PtrSize*8 - 8))if top < minTopHash {top += minTopHash}var inserti *uint8var insertk unsafe.Pointervar val unsafe.Pointerfor {for i := uintptr(0); i < bucketCnt; i++ {if b.tophash[i] != top {if b.tophash[i] == empty && inserti == nil {inserti = &b.tophash[i]insertk = add(unsafe.Pointer(b), dataOffset+i*uintptr(t.keysize))val = add(unsafe.Pointer(b), dataOffset+bucketCnt*uintptr(t.keysize)+i*uintptr(t.valuesize))}continue}k := add(unsafe.Pointer(b), dataOffset+i*uintptr(t.keysize))if t.indirectkey {k = *((*unsafe.Pointer)(k))}if !alg.equal(key, k) {continue}if t.needkeyupdate {typedmemmove(t.key, k, key)}val = add(unsafe.Pointer(b), dataOffset+bucketCnt*uintptr(t.keysize)+i*uintptr(t.valuesize))goto done}ovf := b.overflow(t)if ovf == nil {break}b = ovf}if !h.growing() && (overLoadFactor(int64(h.count), h.B) || tooManyOverflowBuckets(h.noverflow, h.B)) {hashGrow(t, h)goto again}if inserti == nil {newb := h.newoverflow(t, b)inserti = &newb.tophash[0]insertk = add(unsafe.Pointer(newb), dataOffset)val = add(insertk, bucketCnt*uintptr(t.keysize))}if t.indirectkey {kmem := newobject(t.key)*(*unsafe.Pointer)(insertk) = kmeminsertk = kmem}if t.indirectvalue {vmem := newobject(t.elem)*(*unsafe.Pointer)(val) = vmem}typedmemmove(t.key, insertk, key)*inserti = toph.count++done:if h.flags&hashWriting == 0 {throw("concurrent map writes")}h.flags &^= hashWritingif t.indirectvalue {val = *((*unsafe.Pointer)(val))}return val}
插入 key 的过程中和查找 key 有几点不同,需要注意:
- 如果找到要插入的 key ,只需要直接更新对应的 value 值就好了。
- 如果没有在 bmap 中没有找到待插入的 key ,这么这时分几种情况。
情况一: bmap 中还有空位,在遍历 bmap 的时候预先标记空位,一旦查找结束也没有找到 key,就把 key 放到预先遍历时候标记的空位上。
情况二:bmap 中已经没有空位了。这个时候 bmap 装的很满了。此时需要检查一次最大负载因子是否已经达到了。如果达到了,立即进行扩容操作。扩容以后在新桶里面插入 key,流程和上述的一致。如果没有达到最大负载因子,那么就在新生成一个 bmap,并把前一个 bmap 的 overflow 指针指向新的 bmap。
- 如果没有在 bmap 中没有找到待插入的 key ,这么这时分几种情况。
- 在扩容过程中,oldbucke t 是被冻结的,查找 key 时会在
oldbucket 中查找,但不会在 oldbucket 中插入数据。如果在
oldbucket 是找到了相应的 key,做法是将它迁移到新 bmap 后加入 evalucated 标记。
- 在扩容过程中,oldbucke t 是被冻结的,查找 key 时会在
其他流程和查找 key 基本一致,这里就不再赘述了。
3. 删除 Key
func mapdelete(t *maptype, h *hmap, key unsafe.Pointer) {if raceenabled && h != nil {callerpc := getcallerpc(unsafe.Pointer(&t))pc := funcPC(mapdelete)racewritepc(unsafe.Pointer(h), callerpc, pc)raceReadObjectPC(t.key, key, callerpc, pc)}if msanenabled && h != nil {msanread(key, t.key.size)}if h == nil || h.count == 0 {return}if h.flags&hashWriting != 0 {throw("concurrent map writes")}alg := t.key.alghash := alg.hash(key, uintptr(h.hash0))h.flags |= hashWritingbucket := hash & (uintptr(1)<<h.B - 1)if h.growing() {growWork(t, h, bucket)}b := (*bmap)(unsafe.Pointer(uintptr(h.buckets) + bucket*uintptr(t.bucketsize)))top := uint8(hash >> (sys.PtrSize*8 - 8))if top < minTopHash {top += minTopHash}for {for i := uintptr(0); i < bucketCnt; i++ {if b.tophash[i] != top {continue}k := add(unsafe.Pointer(b), dataOffset+i*uintptr(t.keysize))k2 := kif t.indirectkey {k2 = *((*unsafe.Pointer)(k2))}if !alg.equal(key, k2) {continue}if t.indirectkey {*(*unsafe.Pointer)(k) = nil} else {typedmemclr(t.key, k)}v := unsafe.Pointer(uintptr(unsafe.Pointer(b)) + dataOffset + bucketCnt*uintptr(t.keysize) + i*uintptr(t.valuesize))if t.indirectvalue {*(*unsafe.Pointer)(v) = nil} else {typedmemclr(t.elem, v)}b.tophash[i] = emptyh.count--goto done}b = b.overflow(t)if b == nil {goto done}}done:if h.flags&hashWriting == 0 {throw("concurrent map writes")}h.flags &^= hashWriting}
删除操作主要流程和查找 key 流程也差不多,找到对应的 key 以后,如果是指针指向原来的 key,就把指针置为 nil。如果是值就清空它所在的内存。还要清理 tophash 里面的值最后把 map 的 key 总个数计数器减 1 。
如果在扩容过程中,删除操作会在扩容以后在新的 bmap 里面删除。
查找的过程依旧会一直遍历到链表的最后一个 bmap 桶。
4. 增量翻倍扩容
这部分算是整个 Map 实现比较核心的部分了。我们都知道 Map 在不断的装载 Key 值的时候,查找效率会变的越来越低,如果此时不进行扩容操作的话,哈希冲突使得链表变得越来越长,性能也就越来越差。扩容势在必行。
但是扩容过程中如果阻断了 Key 值的写入,在处理大数据的时候会导致有一段不响应的时间,如果用在高实时的系统中,那么每次扩容都会卡几秒,这段时间都不能相应任何请求。这种性能明显是不能接受的。所以要既不影响写入,也同时要进行扩容。这个时候就应该增量扩容了。
这里增量扩容其实用途已经很广泛了,之前举例的 Redis 就采用的增量扩容策略。
接下来看看 Go 是怎么进行增量扩容的。
在 Go 的 mapassign 插入 Key 值、mapdelete 删除 key 值的时候都会检查当前是否在扩容中。
func growWork(t *maptype, h *hmap, bucket uintptr) {evacuate(t, h, bucket&h.oldbucketmask())if h.growing() {evacuate(t, h, h.nevacuate)}}
从这里我们可以看到,每次执行一次 growWork 会迁移 2 个桶。一个是当前的桶,这算是局部迁移,另外一个是 hmap 里面指向的 nevacuate 的桶,这算是增量迁移。
在插入 Key 值的时候,如果当前在扩容过程中,oldbucket 是被冻结的,查找时会先在 oldbucket 中查找,但不会在 oldbucket 中插入数据。只有在 oldbucket 找到了相应的 key,那么将它迁移到新 bucket 后加入 evalucated 标记。
在删除 Key 值的时候,如果当前在扩容过程中,优先查找 bucket,即新桶,找到一个以后把它对应的 Key、Value 都置空。如果 bucket 里面找不到,才会去 oldbucket 中去查找。
每次插入 Key 值的时候,都会判断一下当前装载因子是否超过了 6.5,如果达到了这个极限,就立即执行扩容操作 hashGrow。这是扩容之前的准备工作。
func hashGrow(t *maptype, h *hmap) {bigger := uint8(1)if !overLoadFactor(int64(h.count), h.B) {bigger = 0h.flags |= sameSizeGrow}oldbuckets := h.bucketsnewbuckets, nextOverflow := makeBucketArray(t, h.B+bigger)flags := h.flags &^ (iterator | oldIterator)if h.flags&iterator != 0 {flags |= oldIterator}h.B += biggerh.flags = flagsh.oldbuckets = oldbucketsh.buckets = newbucketsh.nevacuate = 0h.noverflow = 0if h.extra != nil && h.extra.overflow[0] != nil {if h.extra.overflow[1] != nil {throw("overflow is not nil")}h.extra.overflow[1] = h.extra.overflow[0]h.extra.overflow[0] = nil}if nextOverflow != nil {if h.extra == nil {h.extra = new(mapextra)}h.extra.nextOverflow = nextOverflow}}
用图表示出它的流程:
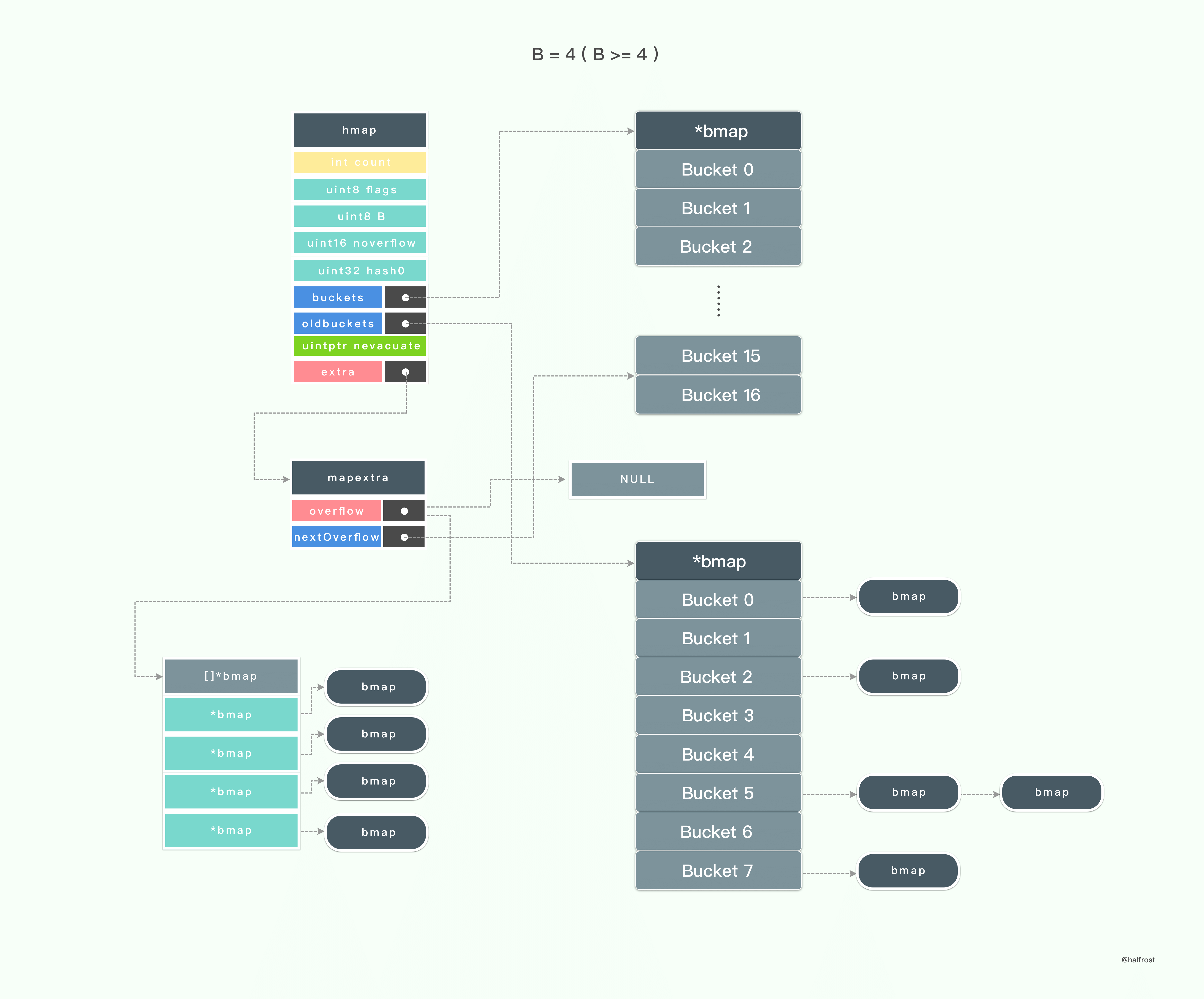
hashGrow 操作算是扩容之前的准备工作,实际拷贝的过程在 evacuate 中。
hashGrow 操作会先生成扩容以后的新的桶数组。新的桶数组的大小是之前的 2 倍。然后 hmap 的 buckets 会指向这个新的扩容以后的桶,而 oldbuckets 会指向当前的桶数组。
处理完 hmap 以后,再处理 mapextra,nextOverflow 的指向原来的 overflow 指针,overflow 指针置为 null。
到此就做好扩容之前的准备工作了。
func evacuate(t *maptype, h *hmap, oldbucket uintptr) {b := (*bmap)(add(h.oldbuckets, oldbucket*uintptr(t.bucketsize)))newbit := h.noldbuckets()alg := t.key.algif !evacuated(b) {var (x, y *bmapxi, yi intxk, yk unsafe.Pointerxv, yv unsafe.Pointer)x = (*bmap)(add(h.buckets, oldbucket*uintptr(t.bucketsize)))xi = 0xk = add(unsafe.Pointer(x), dataOffset)xv = add(xk, bucketCnt*uintptr(t.keysize))if !h.sameSizeGrow() {y = (*bmap)(add(h.buckets, (oldbucket+newbit)*uintptr(t.bucketsize)))yi = 0yk = add(unsafe.Pointer(y), dataOffset)yv = add(yk, bucketCnt*uintptr(t.keysize))}for ; b != nil; b = b.overflow(t) {k := add(unsafe.Pointer(b), dataOffset)v := add(k, bucketCnt*uintptr(t.keysize))for i := 0; i < bucketCnt; i, k, v = i+1, add(k, uintptr(t.keysize)), add(v, uintptr(t.valuesize)) {top := b.tophash[i]if top == empty {b.tophash[i] = evacuatedEmptycontinue}if top < minTopHash {throw("bad map state")}k2 := kif t.indirectkey {k2 = *((*unsafe.Pointer)(k2))}useX := trueif !h.sameSizeGrow() {hash := alg.hash(k2, uintptr(h.hash0))if h.flags&iterator != 0 {if !t.reflexivekey && !alg.equal(k2, k2) {if top&1 != 0 {hash |= newbit} else {hash &^= newbit}top = uint8(hash >> (sys.PtrSize*8 - 8))if top < minTopHash {top += minTopHash}}}useX = hash&newbit == 0}if useX {b.tophash[i] = evacuatedXif xi == bucketCnt {newx := h.newoverflow(t, x)x = newxxi = 0xk = add(unsafe.Pointer(x), dataOffset)xv = add(xk, bucketCnt*uintptr(t.keysize))}x.tophash[xi] = topif t.indirectkey {*(*unsafe.Pointer)(xk) = k2} else {typedmemmove(t.key, xk, k)}if t.indirectvalue {*(*unsafe.Pointer)(xv) = *(*unsafe.Pointer)(v)} else {typedmemmove(t.elem, xv, v)}xi++xk = add(xk, uintptr(t.keysize))xv = add(xv, uintptr(t.valuesize))} else {b.tophash[i] = evacuatedYif yi == bucketCnt {newy := h.newoverflow(t, y)y = newyyi = 0yk = add(unsafe.Pointer(y), dataOffset)yv = add(yk, bucketCnt*uintptr(t.keysize))}y.tophash[yi] = topif t.indirectkey {*(*unsafe.Pointer)(yk) = k2} else {typedmemmove(t.key, yk, k)}if t.indirectvalue {*(*unsafe.Pointer)(yv) = *(*unsafe.Pointer)(v)} else {typedmemmove(t.elem, yv, v)}yi++yk = add(yk, uintptr(t.keysize))yv = add(yv, uintptr(t.valuesize))}}}if h.flags&oldIterator == 0 {b = (*bmap)(add(h.oldbuckets, oldbucket*uintptr(t.bucketsize)))if t.bucket.kind&kindNoPointers == 0 {memclrHasPointers(add(unsafe.Pointer(b), dataOffset), uintptr(t.bucketsize)-dataOffset)} else {memclrNoHeapPointers(add(unsafe.Pointer(b), dataOffset), uintptr(t.bucketsize)-dataOffset)}}}if oldbucket == h.nevacuate {h.nevacuate = oldbucket + 1stop := h.nevacuate + 1024if stop > newbit {stop = newbit}for h.nevacuate != stop && bucketEvacuated(t, h, h.nevacuate) {h.nevacuate++}if h.nevacuate == newbit {h.oldbuckets = nilif h.extra != nil {h.extra.overflow[1] = nil}h.flags &^= sameSizeGrow}}}
上述函数就是迁移过程最核心的拷贝工作了。
整个迁移过程并不难。这里需要说明的是 x ,y 代表的意义。由于扩容以后,新的桶数组是原来桶数组的 2 倍。用 x 代表新的桶数组里面低位的那一半,用 y 代表高位的那一半。其他的变量就是一些标记了,游标和标记 key - value 原来所在的位置。详细的见代码注释。
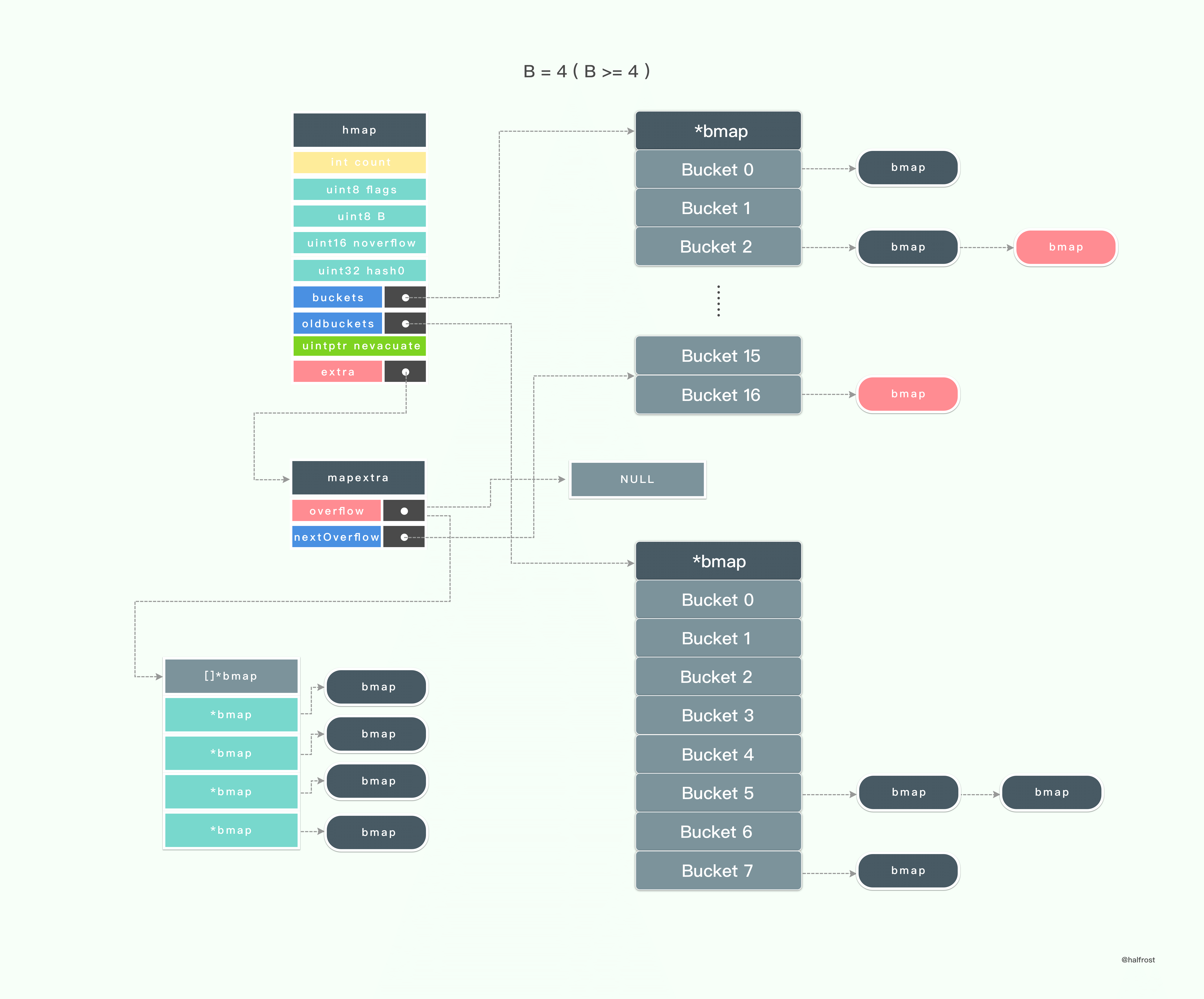
上图中表示了迁移开始之后的过程。可以看到旧的桶数组里面的桶在迁移到新的桶中,并且新的桶也在不断的写入新的 key 值。
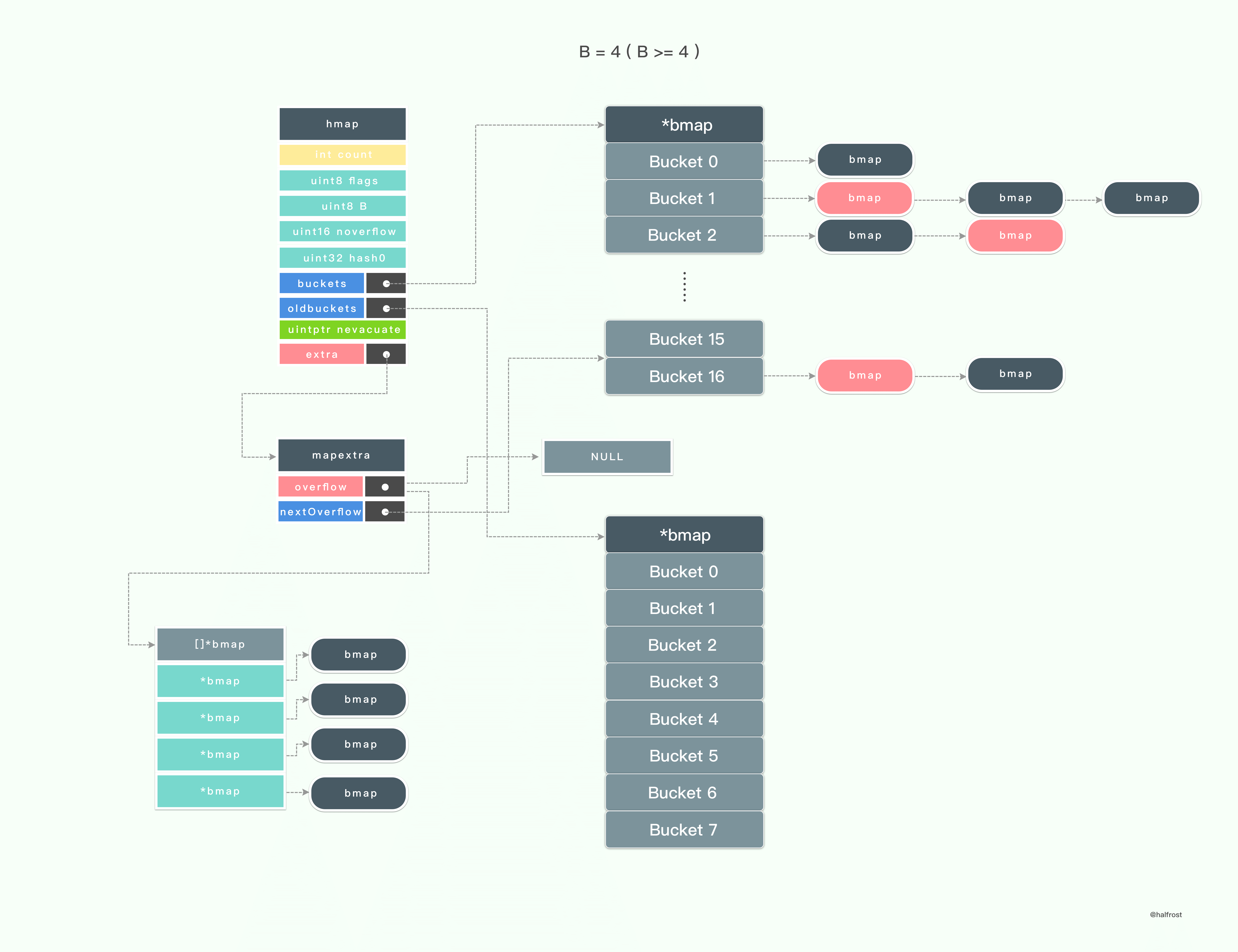
一直拷贝键值对,直到旧桶中所有的键值都拷贝到了新的桶中。
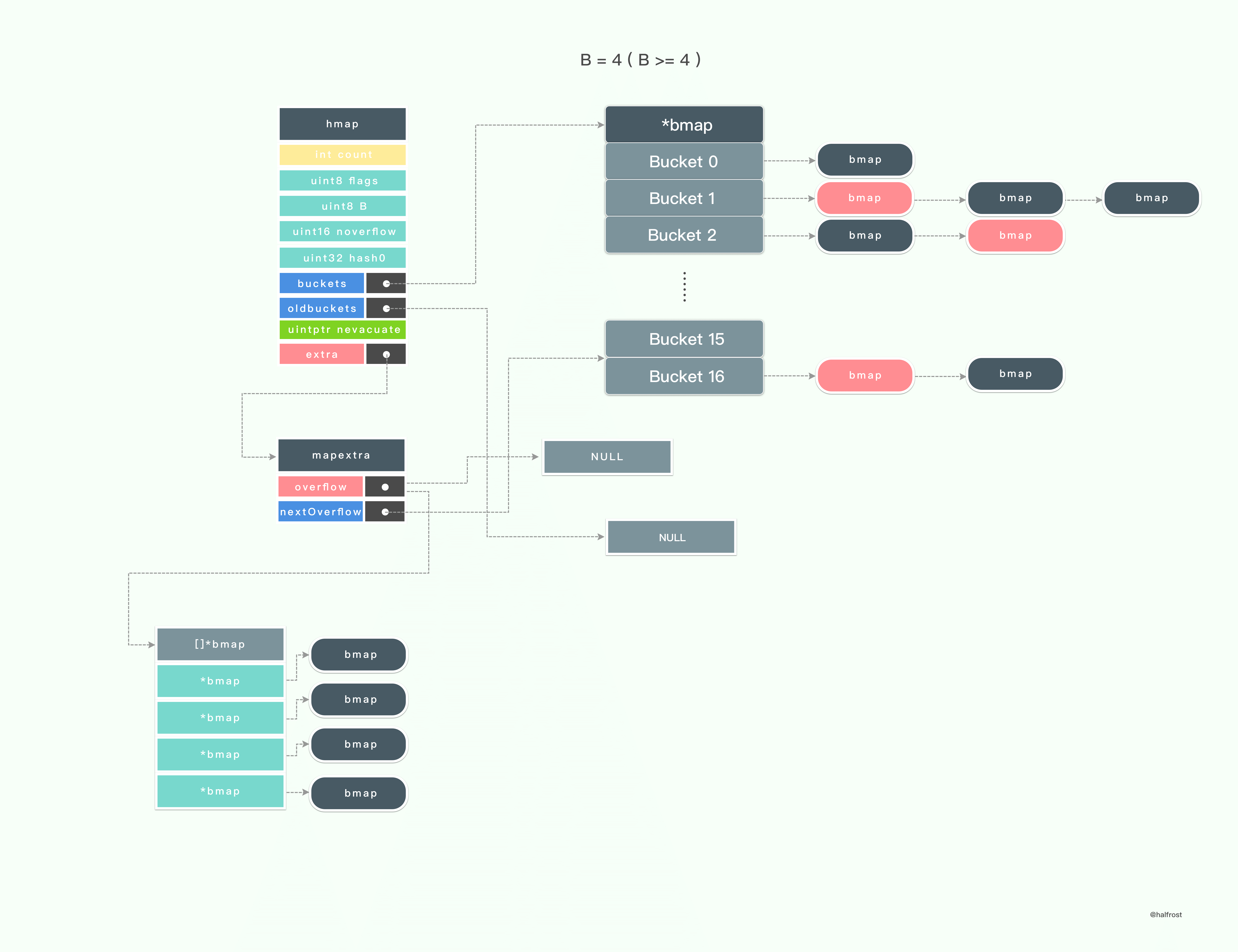
最后一步就是释放旧桶,oldbuckets 的指针置为 null。到此,一次迁移过程就完全结束了。
5. 等量扩容
严格意义上这种方式并不能算是扩容。但是函数名是 Grow,姑且暂时就这么叫吧。
在 go1.8 的版本开始,添加了 sameSizeGrow,当 overflow buckets
的数量超过一定数量 (2^B) 但装载因子又未达到 6.5 的时候,此时可能存在部分空的 bucket,即 bucket 的使用率低,这时会触发 sameSizeGrow,即 B 不变,但走数据迁移流程,将 oldbuckets 的数据重新紧凑排列提高 bucket 的利用率。当然在 sameSizeGrow 过程中,不会触发 loadFactorGrow。
四. Map 实现中的一些优化
读到这里,相信读者心里应该很清楚如何设计并实现一个 Map 了吧。包括 Map 中的各种操作的实现。在探究如何实现一个线程安全的 Map 之前,先把之前说到个一些亮点优化点,小结一下。
在 Redis 中,采用增量式扩容的方式处理哈希冲突。当平均查找长度超过 5 的时候就会触发增量扩容操作,保证 hash 表的高性能。
同时 Redis 采用头插法,保证插入 key 值时候的性能。
在 Java 中,当桶的个数超过了 64 个以后,并且冲突节点为 8 或者大于 8,这个时候就会触发红黑树转换。这样能保证链表在很长的情况下,查找长度依旧不会太长,并且红黑树保证最差情况下也支持 O(log n) 的时间复杂度。
Java 在迁移之后有一个非常好的设计,只需要比较迁移之后桶个数的最高位是否为 0,如果是 0,key 在新桶内的相对位置不变,如果是 1,则加上桶的旧的桶的个数 oldCap 就可以得到新的位置。
在 Go 中优化的点比较多:
- 哈希算法选用高效的 memhash 算法 和 CPU AES 指令集。AES 指令集充分利用 CPU 硬件特性,计算哈希值的效率超高。
- key - value 的排列设计成 key 放在一起,value 放在一起,而不是 key,value 成对排列。这样方便内存对齐,数据量大了以后节约内存对齐造成的一些浪费。
- key,value 的内存大小超过 128 字节以后自动转成存储一个指针。
- tophash 数组的设计加速了 key 的查找过程。tophash 也被复用,用来标记扩容操作时候的状态。
- 用位运算转换求余操作,m % n ,当 n = 1 <<B 的时候,可以转换成 m & (1 << B - 1) 。
- 增量式扩容。
- 等量扩容,紧凑操作。
- Go 1.9 版本以后,Map 原生就已经支持线程安全。(在下一章中重点讨论这个问题)
当然 Go 中还有一些需要再优化的地方:
- 在迁移的过程中,当前版本不会重用 overflow 桶,而是直接重新申请一个新的桶。这里可以优化成优先重用没有指针指向的 overflow 桶,当没有可用的了,再去申请一个新的。这一点作者已经写在了 TODO 里面了。
- 动态合并多个 empty 的桶。
- 当前版本中没有 shrink 操作,Map 只能增长而不能收缩。这块 Redis 有相关的实现。
(鉴于单篇文章的长度,线程安全部分全部放到下篇去讲,稍后更新下篇)
Reference:
《算法与数据结构》
《Redis 设计与实现》
xxHash
字符串 hash 函数
General Purpose Hash Function Algorithms
Java 8 系列之重新认识 HashMap
GitHub Repo:Halfrost-Field
Follow: halfrost · GitHub
Source: https://halfrost.com/go_map/


