数的表示
计算机中的信息都使用0/1的方式进行表示。要对一个数进行表示,对应有三种编码方式,原码,反码,补码。
在这三种编码方式中,最左边一位为符号位,0表示正数,为1表示负数。
原码
反码
反码要表示正数,与原码相同,要表示负数则取相应的正数二进制值按位求反,如+3原码为0011,则-3的反码表示则为1100
相当于对于负数,用
位二进制数进行反码表示,也就是用
对应的二进制数表示。如对于负数
,用
位反码表示,对应二进制数为
补码
补码中,表示正数与原码相同,表示负数则由对应反码+1,如-3反码为1100,则-3对应补码为1101
相当于对于负数,用
位二进制数进行反码表示,也就是用
对应的二进制数表示。如对于负数
,用
位反码表示,对应二进制数为
如下表,对于同样的二进制串,表示的十进制数是不同的。
| 原码 | 反码 | 补码 | |
|---|---|---|---|
| 0111 | +7 | +7 | +7 |
| 0110 | +6 | +6 | +6 |
| 0101 | +5 | +5 | +5 |
| 0100 | +4 | +4 | +4 |
| 0011 | +3 | +3 | +3 |
| 0010 | +2 | +2 | +2 |
| 0001 | +1 | +1 | +1 |
| 0000 | +0 | +0 | +0 |
| 1000 | -0 | -7 | -8 |
| 1001 | -1 | -6 | -7 |
| 1010 | -2 | -5 | -6 |
| 1011 | -3 | -4 | -5 |
| 1100 | -4 | -3 | -4 |
| 1101 | -5 | -2 | -3 |
| 1110 | -6 | -1 | -2 |
| 1111 | -7 | -0 | -1 |
值得注意的是,在反码和原码中,0有正负之分,而在补码中则只有一个0,同时4位补码中可额外表示数-8,在反码和原码中则无法表示。
数的运算
数进行表示之后,下一步就是进行运算。
对于三种表示方式,进行加减运算方式有些不同。
对于原码,考虑数+7(0111)与-5(1101)两者进行加法运算,即+7(0111)+(-5(1101))=+2(0010),我们发现,用原码进行操作,无法很直观的用二进制加减法由0111与1101得到结果0010。
对于反码,同样考虑两者进行加法运算+7(0111)与-5(1010),+7(0111)+(-5(1010))=+2(0010),用反码操作,确实可以操作了
对于补码+7(0111)+(-5(1011))=+2(0010),用补码操作
相对于反码来说,更方便些,并且补码不存在+0与-0的差异。
我的几点疑问
- CPU为何只有加法器(减法可以用加法实现),目前初步找到的资料显示,因为成本(减法器相比加法器要复杂,而且只是用使用加法器进行运算,更统一成一体,更简洁?)
- 补码的由来,目前找到的资料显示,现代计算机中补码是由冯诺伊曼引入的,补码早期使用是帕斯卡在机械式计算器应用的十进制补码。
关于补码的理解
考虑数学中的取模运算。描述正整数mod N加法的有效图示方式是使用具有N个值的圆。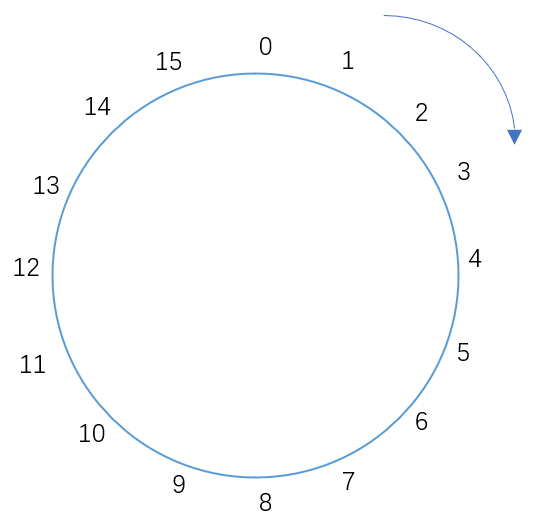
对于数7,计算(7+4) mod 16,找到7所在的位置,顺数4个数,得到结果11。
对于数13,计算(13+4) mod 16,找到 13 所在的位置,顺数4个数,得到结果1。
将上面的运算技巧放到二进制加减上,如将+7加到-3上。首先找到-3对应的二进制数,1101要+7,顺时针数七个数,得到4,对应0100,即为补码加法结果。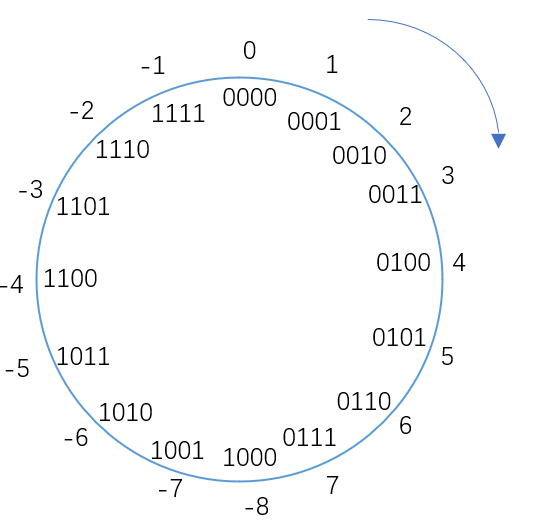
即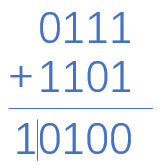
当然,这些二进制数的运算的并不是普适的,对于4位表示,其反码表示的范围是-8~+7,对于结果超过范围的数运算则会得到错误的结果,如对于数+6与+3相加,得到结果是+9,从圆选中数+6(0110),得到的是-7(1001)。
对于减法运算X-Y也是用X补码,然后取(-Y)的补码,即X+(-Y)即得到结果用加法方式进行运算。
数的溢出
实际上,数的运算,如+7与+5,得到结果+12超出表示范围,就发生了算术溢出,有这样几个结论
- 对与有符号数的运算,不同符号的加法运算,不会溢出,同符号加法才会溢出
- 对于俩个数,符号位的进位并不能说明发生溢出。
- 溢出检测的方法,测试两个加数X+Y的符号,以及结果的符号。若X+Y符号为相同,而结果符号与X,Y相反,则发生溢出。

