微分方程

普通应对策略

分离变量，降阶
如
%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-75%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%22850%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(1628%2C0)%22%3E%0A%3Cg%20transform%3D%22translate(397%2C0)%22%3E%0A%3Crect%20stroke%3D%22none%22%20width%3D%22692%22%20height%3D%2260%22%20x%3D%220%22%20y%3D%22220%22%3E%3C%2Frect%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-79%22%20x%3D%2297%22%20y%3D%22725%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%2260%22%20y%3D%22-686%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=u%3D%5Cfrac%7By%7D%7Bx%7D&id=zKlMp)
伯努利




②

一阶线性齐次微分方程

%5Cmathrm%20dx%20%2B%20C_1%3C%2Ftitle%3E%0A%3Cdefs%20aria-hidden%3D%22true%22%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-6C%22%20d%3D%22M42%2046H56Q95%2046%20103%2060V68Q103%2077%20103%2091T103%20124T104%20167T104%20217T104%20272T104%20329Q104%20366%20104%20407T104%20482T104%20542T103%20586T103%20603Q100%20622%2089%20628T44%20637H26V660Q26%20683%2028%20683L38%20684Q48%20685%2067%20686T104%20688Q121%20689%20141%20690T171%20693T182%20694H185V379Q185%2062%20186%2060Q190%2052%20198%2049Q219%2046%20247%2046H263V0H255L232%201Q209%202%20183%202T145%203T107%203T57%201L34%200H26V46H42Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-6E%22%20d%3D%22M41%2046H55Q94%2046%20102%2060V68Q102%2077%20102%2091T102%20122T103%20161T103%20203Q103%20234%20103%20269T102%20328V351Q99%20370%2088%20376T43%20385H25V408Q25%20431%2027%20431L37%20432Q47%20433%2065%20434T102%20436Q119%20437%20138%20438T167%20441T178%20442H181V402Q181%20364%20182%20364T187%20369T199%20384T218%20402T247%20421T285%20437Q305%20442%20336%20442Q450%20438%20463%20329Q464%20322%20464%20190V104Q464%2066%20466%2059T477%2049Q498%2046%20526%2046H542V0H534L510%201Q487%202%20460%202T422%203Q319%203%20310%200H302V46H318Q379%2046%20379%2062Q380%2064%20380%20200Q379%20335%20378%20343Q372%20371%20358%20385T334%20402T308%20404Q263%20404%20229%20370Q202%20343%20195%20315T187%20232V168V108Q187%2078%20188%2068T191%2055T200%2049Q221%2046%20249%2046H265V0H257L234%201Q210%202%20183%202T145%203Q42%203%2033%200H25V46H41Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-7C%22%20d%3D%22M139%20-249H137Q125%20-249%20119%20-235V251L120%20737Q130%20750%20139%20750Q152%20750%20159%20735V-235Q151%20-249%20141%20-249H139Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-79%22%20d%3D%22M21%20287Q21%20301%2036%20335T84%20406T158%20442Q199%20442%20224%20419T250%20355Q248%20336%20247%20334Q247%20331%20231%20288T198%20191T182%20105Q182%2062%20196%2045T238%2027Q261%2027%20281%2038T312%2061T339%2094Q339%2095%20344%20114T358%20173T377%20247Q415%20397%20419%20404Q432%20431%20462%20431Q475%20431%20483%20424T494%20412T496%20403Q496%20390%20447%20193T391%20-23Q363%20-106%20294%20-155T156%20-205Q111%20-205%2077%20-183T43%20-117Q43%20-95%2050%20-80T69%20-58T89%20-48T106%20-45Q150%20-45%20150%20-87Q150%20-107%20138%20-122T115%20-142T102%20-147L99%20-148Q101%20-153%20118%20-160T152%20-167H160Q177%20-167%20186%20-165Q219%20-156%20247%20-127T290%20-65T313%20-9T321%2021L315%2017Q309%2013%20296%206T270%20-6Q250%20-11%20231%20-11Q185%20-11%20150%2011T104%2082Q103%2089%20103%20113Q103%20170%20138%20262T173%20379Q173%20380%20173%20381Q173%20390%20173%20393T169%20400T158%20404H154Q131%20404%20112%20385T82%20344T65%20302T57%20280Q55%20278%2041%20278H27Q21%20284%2021%20287Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-3D%22%20d%3D%22M56%20347Q56%20360%2070%20367H707Q722%20359%20722%20347Q722%20336%20708%20328L390%20327H72Q56%20332%2056%20347ZM56%20153Q56%20168%2072%20173H708Q722%20163%20722%20153Q722%20140%20707%20133H70Q56%20140%2056%20153Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJSZ2-222B%22%20d%3D%22M114%20-798Q132%20-824%20165%20-824H167Q195%20-824%20223%20-764T275%20-600T320%20-391T362%20-164Q365%20-143%20367%20-133Q439%20292%20523%20655T645%201127Q651%201145%20655%201157T672%201201T699%201257T733%201306T777%201346T828%201360Q884%201360%20912%201325T944%201245Q944%201220%20932%201205T909%201186T887%201183Q866%201183%20849%201198T832%201239Q832%201287%20885%201296L882%201300Q879%201303%20874%201307T866%201313Q851%201323%20833%201323Q819%201323%20807%201311T775%201255T736%201139T689%20936T633%20628Q574%20293%20510%20-5T410%20-437T355%20-629Q278%20-862%20165%20-862Q125%20-862%2092%20-831T55%20-746Q55%20-711%2074%20-698T112%20-685Q133%20-685%20150%20-700T167%20-741Q167%20-789%20114%20-798Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2212%22%20d%3D%22M84%20237T84%20250T98%20270H679Q694%20262%20694%20250T679%20230H98Q84%20237%2084%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-50%22%20d%3D%22M287%20628Q287%20635%20230%20637Q206%20637%20199%20638T192%20648Q192%20649%20194%20659Q200%20679%20203%20681T397%20683Q587%20682%20600%20680Q664%20669%20707%20631T751%20530Q751%20453%20685%20389Q616%20321%20507%20303Q500%20302%20402%20301H307L277%20182Q247%2066%20247%2059Q247%2055%20248%2054T255%2050T272%2048T305%2046H336Q342%2037%20342%2035Q342%2019%20335%205Q330%200%20319%200Q316%200%20282%201T182%202Q120%202%2087%202T51%201Q33%201%2033%2011Q33%2013%2036%2025Q40%2041%2044%2043T67%2046Q94%2046%20127%2049Q141%2052%20146%2061Q149%2065%20218%20339T287%20628ZM645%20554Q645%20567%20643%20575T634%20597T609%20619T560%20635Q553%20636%20480%20637Q463%20637%20445%20637T416%20636T404%20636Q391%20635%20386%20627Q384%20621%20367%20550T332%20412T314%20344Q314%20342%20395%20342H407H430Q542%20342%20590%20392Q617%20419%20631%20471T645%20554Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-28%22%20d%3D%22M94%20250Q94%20319%20104%20381T127%20488T164%20576T202%20643T244%20695T277%20729T302%20750H315H319Q333%20750%20333%20741Q333%20738%20316%20720T275%20667T226%20581T184%20443T167%20250T184%2058T225%20-81T274%20-167T316%20-220T333%20-241Q333%20-250%20318%20-250H315H302L274%20-226Q180%20-141%20137%20-14T94%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-78%22%20d%3D%22M52%20289Q59%20331%20106%20386T222%20442Q257%20442%20286%20424T329%20379Q371%20442%20430%20442Q467%20442%20494%20420T522%20361Q522%20332%20508%20314T481%20292T458%20288Q439%20288%20427%20299T415%20328Q415%20374%20465%20391Q454%20404%20425%20404Q412%20404%20406%20402Q368%20386%20350%20336Q290%20115%20290%2078Q290%2050%20306%2038T341%2026Q378%2026%20414%2059T463%20140Q466%20150%20469%20151T485%20153H489Q504%20153%20504%20145Q504%20144%20502%20134Q486%2077%20440%2033T333%20-11Q263%20-11%20227%2052Q186%20-10%20133%20-10H127Q78%20-10%2057%2016T35%2071Q35%20103%2054%20123T99%20143Q142%20143%20142%20101Q142%2081%20130%2066T107%2046T94%2041L91%2040Q91%2039%2097%2036T113%2029T132%2026Q168%2026%20194%2071Q203%2087%20217%20139T245%20247T261%20313Q266%20340%20266%20352Q266%20380%20251%20392T217%20404Q177%20404%20142%20372T93%20290Q91%20281%2088%20280T72%20278H58Q52%20284%2052%20289Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-29%22%20d%3D%22M60%20749L64%20750Q69%20750%2074%20750H86L114%20726Q208%20641%20251%20514T294%20250Q294%20182%20284%20119T261%2012T224%20-76T186%20-143T145%20-194T113%20-227T90%20-246Q87%20-249%2086%20-250H74Q66%20-250%2063%20-250T58%20-247T55%20-238Q56%20-237%2066%20-225Q221%20-64%20221%20250T66%20725Q56%20737%2055%20738Q55%20746%2060%20749Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-64%22%20d%3D%22M376%20495Q376%20511%20376%20535T377%20568Q377%20613%20367%20624T316%20637H298V660Q298%20683%20300%20683L310%20684Q320%20685%20339%20686T376%20688Q393%20689%20413%20690T443%20693T454%20694H457V390Q457%2084%20458%2081Q461%2061%20472%2055T517%2046H535V0Q533%200%20459%20-5T380%20-11H373V44L365%2037Q307%20-11%20235%20-11Q158%20-11%2096%2050T34%20215Q34%20315%2097%20378T244%20442Q319%20442%20376%20393V495ZM373%20342Q328%20405%20260%20405Q211%20405%20173%20369Q146%20341%20139%20305T131%20211Q131%20155%20138%20120T173%2059Q203%2026%20251%2026Q322%2026%20373%20103V342Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-2B%22%20d%3D%22M56%20237T56%20250T70%20270H369V420L370%20570Q380%20583%20389%20583Q402%20583%20409%20568V270H707Q722%20262%20722%20250T707%20230H409V-68Q401%20-82%20391%20-82H389H387Q375%20-82%20369%20-68V230H70Q56%20237%2056%20250Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMATHI-43%22%20d%3D%22M50%20252Q50%20367%20117%20473T286%20641T490%20704Q580%20704%20633%20653Q642%20643%20648%20636T656%20626L657%20623Q660%20623%20684%20649Q691%20655%20699%20663T715%20679T725%20690L740%20705H746Q760%20705%20760%20698Q760%20694%20728%20561Q692%20422%20692%20421Q690%20416%20687%20415T669%20413H653Q647%20419%20647%20422Q647%20423%20648%20429T650%20449T651%20481Q651%20552%20619%20605T510%20659Q484%20659%20454%20652T382%20628T299%20572T226%20479Q194%20422%20175%20346T156%20222Q156%20108%20232%2058Q280%2024%20350%2024Q441%2024%20512%2092T606%20240Q610%20253%20612%20255T628%20257Q648%20257%20648%20248Q648%20243%20647%20239Q618%20132%20523%2055T319%20-22Q206%20-22%20128%2053T50%20252Z%22%3E%3C%2Fpath%3E%0A%3Cpath%20stroke-width%3D%221%22%20id%3D%22E1-MJMAIN-31%22%20d%3D%22M213%20578L200%20573Q186%20568%20160%20563T102%20556H83V602H102Q149%20604%20189%20617T245%20641T273%20663Q275%20666%20285%20666Q294%20666%20302%20660V361L303%2061Q310%2054%20315%2052T339%2048T401%2046H427V0H416Q395%203%20257%203Q121%203%20100%200H88V46H114Q136%2046%20152%2046T177%2047T193%2050T201%2052T207%2057T213%2061V578Z%22%3E%3C%2Fpath%3E%0A%3C%2Fdefs%3E%0A%3Cg%20stroke%3D%22currentColor%22%20fill%3D%22currentColor%22%20stroke-width%3D%220%22%20transform%3D%22matrix(1%200%200%20-1%200%200)%22%20aria-hidden%3D%22true%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-6C%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-6E%22%20x%3D%22278%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-7C%22%20x%3D%221001%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-79%22%20x%3D%221280%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-7C%22%20x%3D%221777%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-3D%22%20x%3D%222333%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJSZ2-222B%22%20x%3D%223390%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2212%22%20x%3D%224501%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-50%22%20x%3D%225279%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-28%22%20x%3D%226031%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%226420%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-29%22%20x%3D%226993%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-64%22%20x%3D%227382%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-78%22%20x%3D%227939%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMAIN-2B%22%20x%3D%228734%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%3Cg%20transform%3D%22translate(9734%2C0)%22%3E%0A%20%3Cuse%20xlink%3Ahref%3D%22%23E1-MJMATHI-43%22%20x%3D%220%22%20y%3D%220%22%3E%3C%2Fuse%3E%0A%20%3Cuse%20transform%3D%22scale(0.707)%22%20xlink%3Ahref%3D%22%23E1-MJMAIN-31%22%20x%3D%221011%22%20y%3D%22-213%22%3E%3C%2Fuse%3E%0A%3C%2Fg%3E%0A%3C%2Fg%3E%0A%3C%2Fsvg%3E#card=math&code=%5Cln%20%7Cy%7C%3D%5Cint%20-P%28x%29%5Cmathrm%20dx%20%2B%20C_1&id=uWSsp)

一阶线性非齐次微分方程

可能的正向思路

不难发现，中间得到的,正好就是对应齐次微分方程的通解，因此可以先求齐次通解再用常数变易法求解。

二阶线性解的结构

① 若为齐次的线性无关特解，则为齐次方程的通解
②若为齐次方程的通解，为非齐次方程的一个特解，则为非齐次线性方程的通解
③叠加原理，若分别为与的两个特解，则为的一个特解

二阶齐次

已知一特解求通解

将y=uv的方式推广到二阶非齐次

显然这个思路是可以推到n阶的
不过用这样的方式，求解一个重点就是与中的求解,这实际上就是求对应齐次方程的两个特解
剩下来就是联立求解。实际题目中，往往会给出齐次方程的一个特解或是通解，只需求得即可。

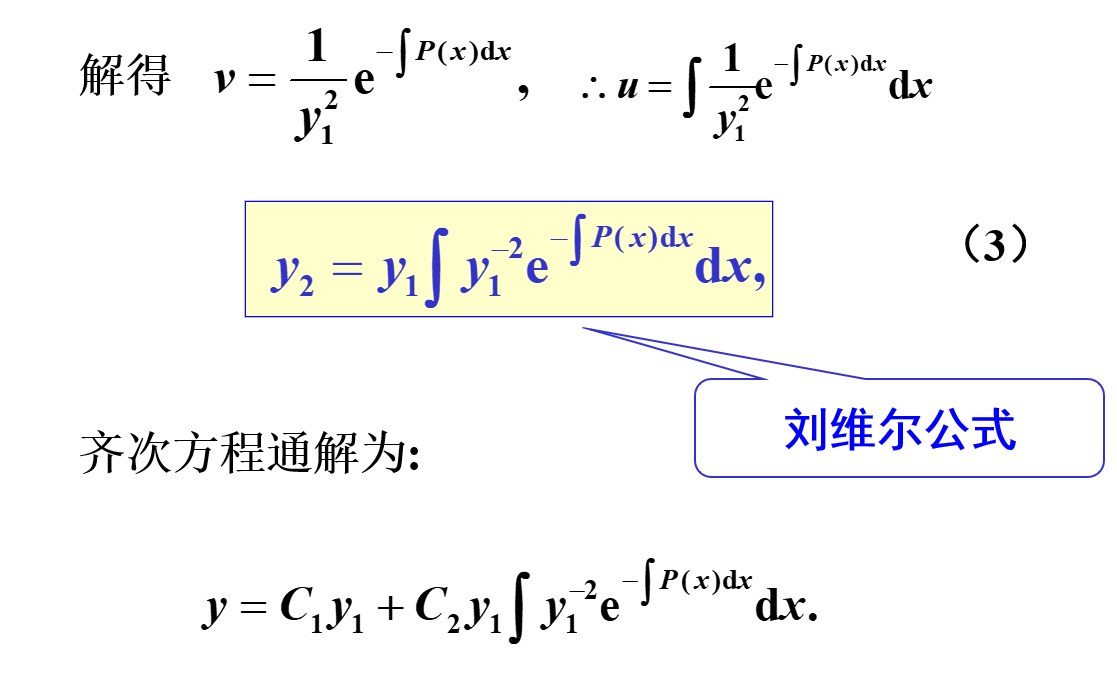
已知二阶齐次方程的通解

不正好就是这个方程的两个特解吗？
看看上面的内容，对比一下，正好就可以匹配，剩下的部分就是

可解得

已知二阶齐次方程一特解

这儿
令


代入原方程



特解可以代换


令
原方程则变成了一个一阶非齐次线性方程

二阶常系数齐次

这是二阶齐次的特殊情况，但是很具有讨论意义，均为常数，不难猜测是很符合要求的
代入原方程

特征方程
①，得两特解，通解为
②,得一特解,剩余一根，代入，其中

又

因此通解即为
得到结论另外一个特解为
③，
欧拉公式
两特解


根据解的叠加原理

即通解
结论
对于特征方程

特征根	通解

:::info


有

:::

二阶常系数非齐次

求解非齐次特解

情况一

设，其中为多项式

对于特征方程
① 不为特征方程的根
则
因此可以认为为m次多项式，即可设
② 为特征方程的单根

因此可以认为为m+1次多项式，即可设
③ 为特征方程的重根

因此可以认为为m+2次多项式，即可设
随后使用待定系数法即可得到特解

情况二

根据欧拉公式

根据解的叠加原理
可以令

则求解这两个微分方程的特解可以得到原微分方程的特解


根据情况一中的计算

如果,则
此时可设
否则
此时可设
可得

如果,则
此时可设
否则
此时可设
可得

其中
再次使用欧拉公式

因为共轭关系,可以拆开该式子消除复数部分
即
在解该类型时,可假设,随后使用待定系数法求解
推广n阶,只需考虑的变化,是与作为特征方程的根的次数有关的

欧拉方程

令

使用记号表示对求导
则


原方程转为

此时即为关于t的n阶常系数非齐次微分方程