汤家凤-函数与极限

函数

三要素

• 定义域
• 值域

• 映射关系 :::info 反函数存在，对应区间上必须(严格)单调 ::: 基本初等函数

• 

• 
• 
• 
• 

初等函数=常数与基本初等函数进行有限次的四则运算与复合运算
基本性质

• 有界

定义

• 单调

定义

• 奇偶

定义

• 周期

定义

极限

定义

case1：

case2：

case3：



:::warning 明确

①
x趋近于a，意味着x永远取不到a
eg:

②
eg:

③ 去心领域

是这两个开区间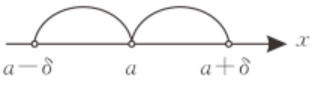

④
⑤ 关于
以上各种各样的定义中，承担的是一个误差的角色，因为是任意取的，要多小有多小，如果有也就是，与的距离，要多小有多小，也就是两者是无限接近的!自然而然有，那么我们不必拘泥于极限定义，核心是极限的本质，无限接近。我们也可以用其本质去重新定义极限，不过是可以但没必要 :::

无穷小

定义

:::warning ① 0 是不是无穷小?

② 是不是无穷小?

从上面两个，可以看出无穷小的本质，是函数 :::

无穷小的层次

设
①

②
:::info eg:



::: ③

极限的性质

一般性质

① 唯一性，指若函数在某点的极限存在，则必唯一，否则极限不存在
② 保号性，设 :::info eg:

::: ③ 有界性(数列)
:::info

/ :::

存在性质

① 准则一：夹逼定理 :::info eg:




:::

类型一，n项和求极限

① 先和后极限 :::info eg:

::: ② 夹逼定理 :::info eg1:

eg2:

::: ③ 定积分定义(分子分母均齐次，分母多一次)
:::info eg1:

eg2:

::: ②准则二：单调有界的数列，必有极限

• 
• 

  类型二，极限存在性证明

  :::info eg:
  ，证明
  
  
  数学归纳法
  
  注意:此处2的取值是值得讨论的,考虑为什么是2
  
  
  
  
  
  
  
  eg:
  
  
  
  
  
  eg:
  
  
  

得到一个模板
证明极限存在的核心是
找到其单调性与对应的一个上界或下界
① 找出可能的递推关系
② 找出单调性

③ 找出界
不等式公式，数学归纳法
④ 可能的话可以求出极限
当极限存在时，可以根据递推关系求 :::

无穷小的性质

一般性质
①
②
③
等价性质
①
②
常用等价




拓展等价，较为重要(快速解题必备，需要经验积累

:::info 一些结论



:::

两个重要极限

类型三，不定型极限

应对策略
①适当的变形
提取，分子有理化等

②等价无穷小 :::info 等价无穷小使用时机，乘法是安全，随便用，加减法不安全，多加考虑 ::: ③洛必达
:::info eg:
:::
:::info eg:
:::
:::info



:::
转换为

连续与间断

定义

连续
①
②
间断

① 第一类

• 可去间断点=左右极限存在且相等
• 跳跃间断点=左右极限存在但不等

② 第二类

• 无穷间断点= 左右极限中至少有一个为无穷大
• 振荡间断点= 振荡不存在，如
• other

  类型四，间断点分类

  闭区间连续的性质

  

  最值

  

  有界

  

  零点定理

  

  界值定理

  
  

:::info ① ，开区间，可以考虑使用零点定理
② ，闭区间或是函数值之和，可以考虑界值定理 :::

小结

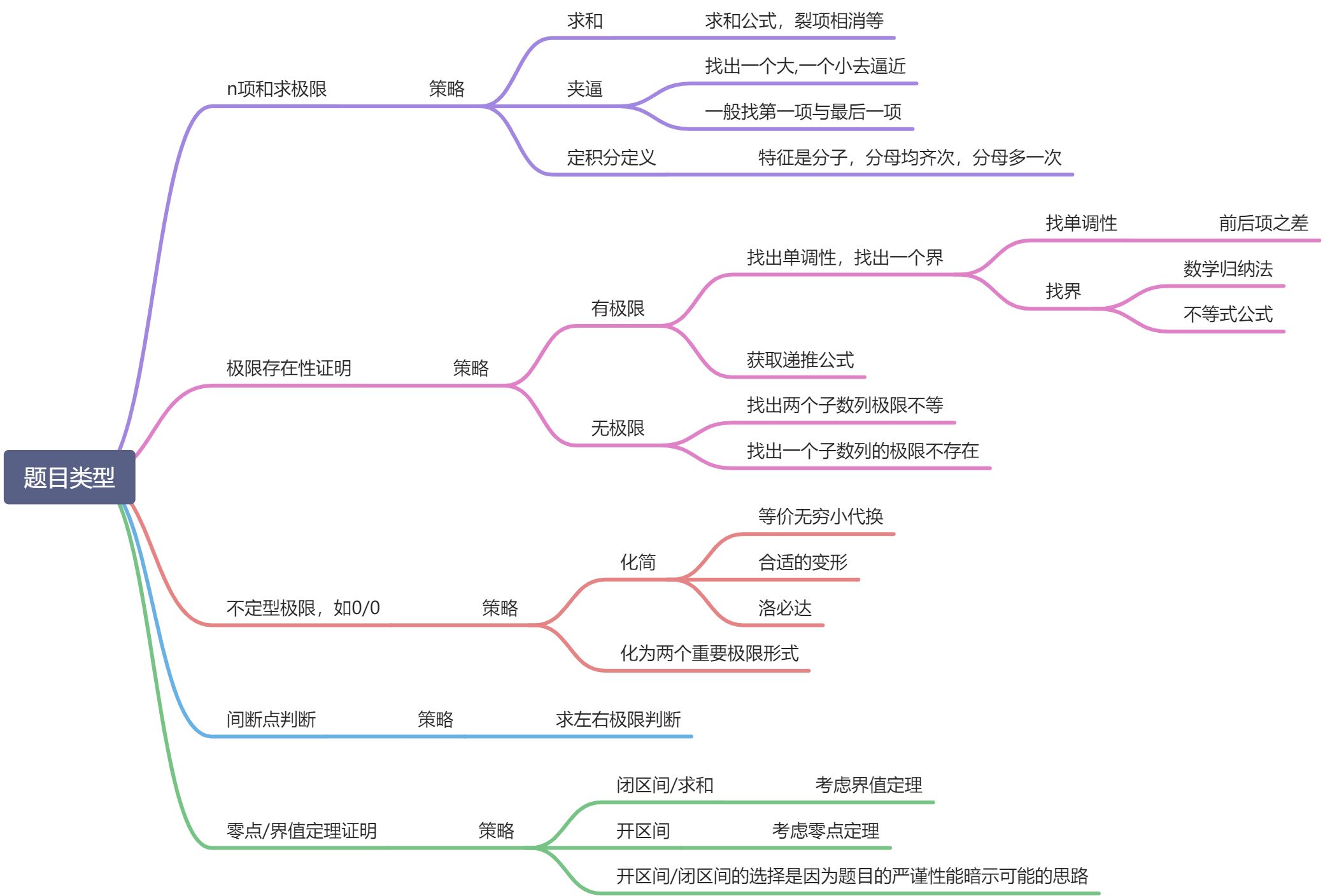:::info some tips
面对极限中的根式，可以考虑将其部分有理化，也可以考虑使用不等式公式将根号去掉 :::