單變數：y = mx + b
如鞋碼和身高的關係
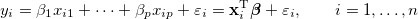
image.png

多變數：

image.png

Least Squares Fitting 最小二乘擬合

需要兩個矩陣 matX 和 matY，matX 保存訓練集的所有輸入，matY 保存理想輸出

因為矩陣中每個輸入都附帶一個常數 1，便於計算「截距」，因此行數等於輸入維度 + 1
matY 保存的是輸出，因此只有 1 行

用到「矩陣分解」

將攝氏度轉為華氏度的訓練資料：

  1. 0        -> 32
  2. 100    -> 212

matX

  1. 0.0, 1.0
  2. 100.0, 1.0

matY

  1. 32.0
  2. 212.0

根據 matY，用 QR 分解來分解 matX，得到矩陣：

  1. 1.8
  2. 32.0

因此 f = c * 1.8 + 32

Anscombe’s Quartet 安斯庫姆四重奏

一個指出線性回歸問題所在的資料集：

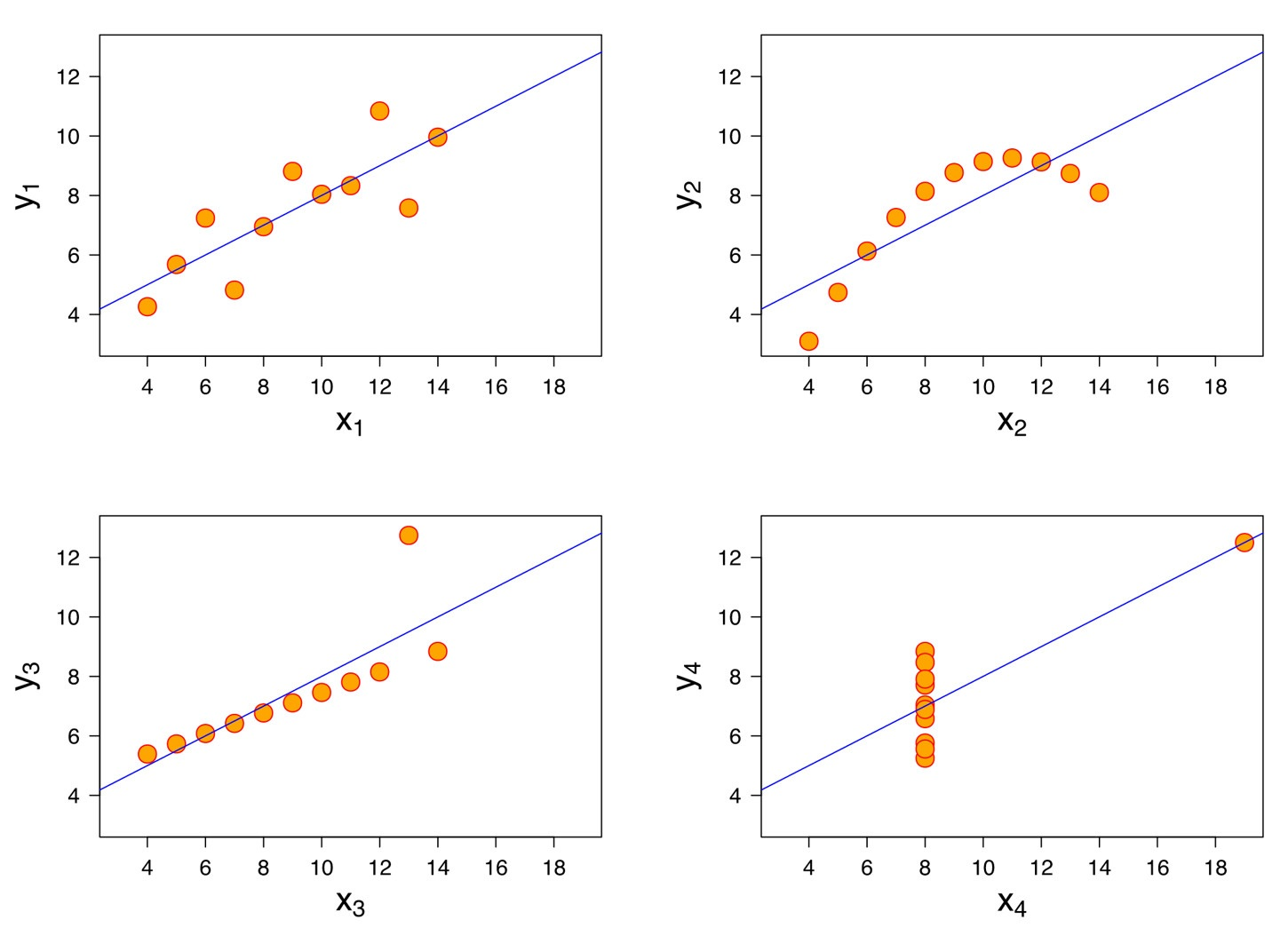
image.png
上述四個資料集線性回歸擬合出的結果是相同的

X1 是一般的線性回歸，X2 的資料為非線性
X3 和 X4 表示「離群值」的影響