TSP 是傳統迭代演算法難以求解的 NP-Hard 問題，因此經常用模擬退火演算法來解決。
問題描述
有一個旅行商，在指定的多個城市中，從任意一個開始，分別經過其他城市，並最終回到起點，除了起點之外的城市能且僅能經過一次。求最短的路徑。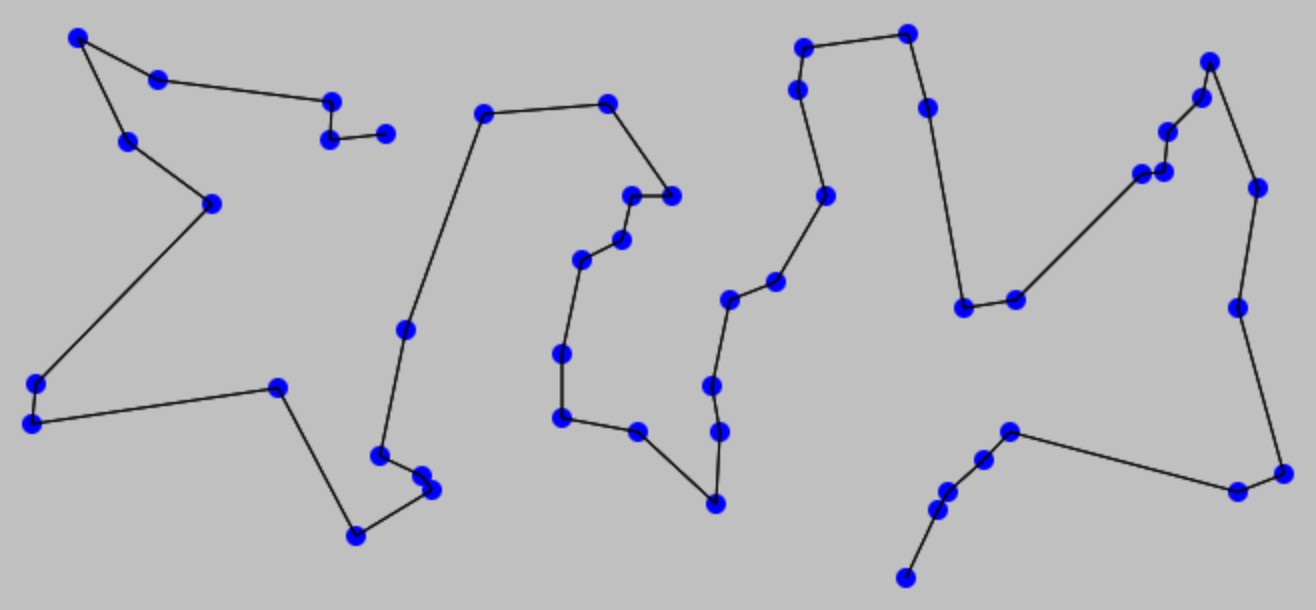
還有一些變體，如不需回到起點，可以多次經過同一個城市，或是城市之間的雙向路徑成本不同……
這裡我們只探討每個城市僅經過一次，且不返回起點的情況。
如果採用蠻力，則相當於全排列，需要搜索的數量是 n!
模擬退火法
考慮模擬退火法，對於連續型資料，我們是在當前解的某個或某幾個維度上加一個隨機值。
而對於離散型資料，則是要選擇一條與當前解接近的旅行路徑
依然是先生成一個初始隨機解，也就是一個有序列表，之後可以通過交換兩個城市的順序來生成新的解。
三要素：
- 評估方法：經過的距離，越小越好
- 生成隨機解：隨機生成
- 從當前解構造新解：交換數組中兩個元素
The Knapsack Problem背包問題
問題描述
一個背包，在商店裡，如何組合貨物，使背包中物品的價值最高？
物品具有重量和價值兩個屬性，背包有負重上限
背包問題的常見形式是所選物品的數目固定，且每樣物品最多選一次，被稱為 「0-1 背包問題」
模擬退火法
解的形式是一個向量，維度等於可以放進背包的物品數量，向量中每個物品對應的元素代表該物品的取用數量（都是整數）
- 評估函數：最小化問題，因此計算理論上的最大總價值和當前總價值的差，優化這個差值最小。此外還要考慮重量，如果重量超過上限，就將評估分數置為一個最大值。
- 生成隨機解：向空背包一個個的放入物品，直到超過上限
- 從當前解構造新解：放入一個之前沒放過的物品，如果超重，就從後向前逐個取出放入的物品
若有收获，就点个赞吧
0 人点赞
