Levels of Measurement

統計學中，資料通常分為兩種類型：性質量 qualitative 和數字量 quantitative

比如描述一杯咖啡，香氣濃郁就是性質量，價格 5 元則是數字量

根據 On the Theory of Scales of Measurement. 一書中的內容，可以將上述兩種資料細分為四個子類

名義量 順序量 區間量 比率量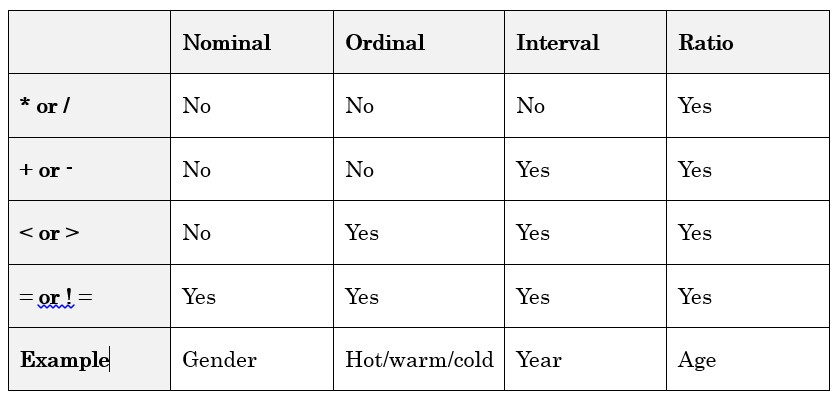
image.png
其中名義量和順序量的觀測值屬於性質量
區間量和比率量的測量值屬於數字量

多數情況下，可以通過運算對資料的適用來判斷對應的類型。

名義量，如顏色，可以判斷兩個顏色是否相等，但顏色的大小無法比較

順序量，如一杯咖啡的「熱度」，可以按照有多熱進行排序，如沸騰、較熱、溫等等

考慮一下美國的郵編，是一個五位數字，對應一個特定區域。 可以比較是否相等，但郵編的大小沒有實際意義，因此是名義量

區間量：沒有固定的 0 點，如 「2013 年」

比率量：有一個明確、固定的 0 作為起點，如年齡

開氏溫度是比率量，沒有比 0 度更低的溫度，10 度是 5 度的 2 倍熱 攝氏/華氏溫度是區間量，10 攝氏度並非 5 攝氏度的 2 倍熱

觀測值歸一化

將資料變換到特定的區間，就是歸一化，機器學習一般要求所有的值都要在某個特定區間，通常是 (-1, 1) 或 (0, 1)

名義量歸一化

一般採用 one-hot 編碼法，如鳶尾花的三種「類別」：

  • Setosa
  • Versicolor
  • Virginica

可以將其編碼為

  • [1,0,0]
  • [0,1,0]
  • [0,0,1]

順序量歸一化

順序量並不一定是數值型，但包含某種順序

如果順序無關緊要，可以採用 one-hot 編碼

若想保持順序，可以給每個類別附一個從 0 開始的整數，計算區間的寬度，用百分比來歸一化

如上學的年級，可以用 「學業完成度」這個百分比進行歸一化
共 14 個等級 f(x) = (n_H-n_L)*(x/N) + n_L
(n_L, n_H) 為歸一化的目標區間，N 原始區間寬度
Preschool (0) 0%
Kindergarten (1) 7
First grade (2) 14
Second grade (3) 21
Third grade (4) 28
Fourth grade (5) 35
Fifth grade (6) 42
Sixth grade (7) 50%
Seventh grade (8) 57
Eighth grade (9) 64
Freshman (10) 71
Sophomore (11) 78
Junior (12) 85
Senior (13) 92
100

解歸一化即為歸一化的逆操作，公式 f(x) = N*(x-n_L)/(n_H-n_L)

數字量歸一化

區間量和比率量的歸一化方法相同，需要知道資料的數值範圍，以及歸一化到的特定區間

然後採用線性插值

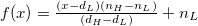
image.png

其他歸一化方法

倒數歸一化

歸一化到 (-1, 1) 之間

f(x) = 1/x

等邊編碼法 Equilateral Encoding

根據作者 2017 年的文章，他已棄用等邊編碼法，當前硬體和算力下，基本沒有提升了

等邊編碼法師 One-hot 的有力替代，有兩個優勢：

  • 輸出通道比 One-hot 少一個（10 個類別，輸出是 9 通道）
  • 傳播誤差的效果比 One-hot 要好

關於第二點的理解，可以認為，100 個類別，採用 One-hot，如果分類錯誤，則誤差主要在兩個通道上，而等邊編碼法，則可以將誤差分在多個通道上

對每個類別，其表示的編碼值可以通過算法計算出，令每組值的歐拉距離相等（因此 n 個類別需要 n-1 個通道）（是多維空間中的柏拉圖多面體！）

二分類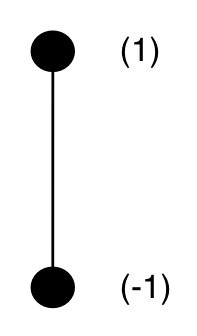
image.png
三個類別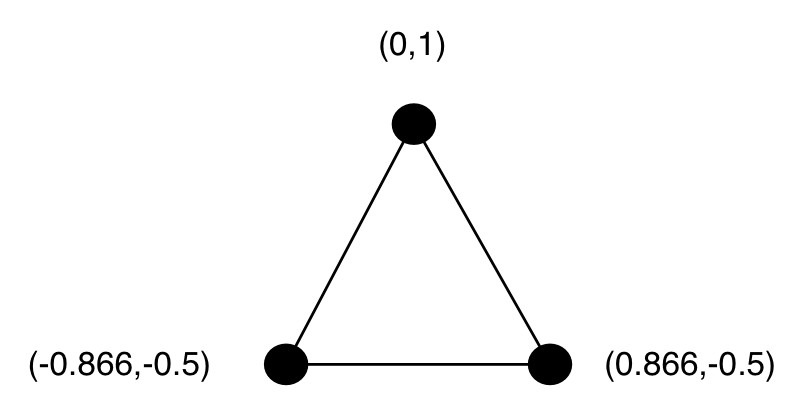
image.png
四個類別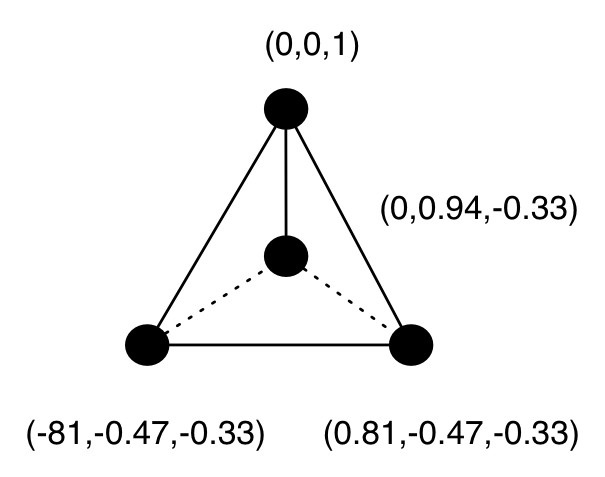
image.png
算法實現：
https://github.com/jeffheaton/aifh/blob/master/vol1/c-examples/Equilateral.c

  1. void Equilat (
  2.    int classCount,
  3.    double low,
  4.    double high,
  5.    double *outputMatrix
  6.    )
  7. {
  8.     int i, j, k, rowSize ;
  9.     double r, f ;
  10.     const double min = -1;
  11.     const double max = 1;
  13.     rowSize = classCount - 1 ;
  15.     /** Seed the initial matrix */
  16.     outputMatrix[0] = -1.0 ;
  17.     outputMatrix[rowSize] = 1.0 ;
  19.     /* Now expand the matrix one for each class */
  20.     for (k=2 ; k<classCount ; k++) {
  21.         r = (double) k;
  22.         f = sqrt ( r * r - 1.0 ) / r ; 
  23.         for (i=0 ; i<k ; i++) {        
  24.             for (j=0 ; j<k-1 ; j++) {     
  25.                 outputMatrix[i*rowSize+j] *= f ;
  26.             }
  27.         }
  28.         r = -1.0 / r ;
  29.         for (i=0 ; i<k ; i++) {
  30.             outputMatrix[i*rowSize+k-1] = r ;
  31.         }
  33.         for (i=0 ; i<k-1 ; i++) {
  34.             outputMatrix[k*rowSize+i] = 0.0 ;
  35.         }
  37.         outputMatrix[k*rowSize+k-1] = 1.0 ;
  38.     }
  40.     /* scale to correct range */
  41.     for (i = 0; i < (rowSize*classCount); i++) {
  42.         outputMatrix[i] = ((outputMatrix[i] - min) / (max - min))
  43.                         * (high - low) + low;
  44.     }
  45. }