種群適應度選擇

理解種群

本書中，種群是解決問題的一組潛在方法。同一問題的一組解，構成的就是所謂的種群。

初始種群

種群規模通常不會隨著算法的進行而改變，是一個硬性限制。如果有 5 個人出生，則必須有 5 個人死亡。

初始種群數目等於種群規模，一般隨機生成初始種群

種群可以是競爭的，也可以是合作的。
競爭種群會創造後代來進行迭代。
合作種群永遠不會添加或刪除成員。

自然界中的種群既有競爭又有合作，而我們受自然啟發的演算法則只能選其一，要麼是競爭的，要麼是合作的

競爭種群

競爭種群的演算法包括遺傳演算法和遺傳編程。

每個個體會被評分，分數較高的個體更有機會被選去交配並留下後代

可能會發生後代的最高分要低於上一代的情況，導致最優解的分數下降

於是一般採用「精英」的設置，選擇一定數目的最優秀個體，直接複製到下一代。這樣演算法永遠都會保留最優解，不會倒退到較差的分數。

合作種群

合作種群的演算法包括粒子群優化（Particle Swarm Optimization, PSO）和蟻群優化（Ant Colony Optimization, ACO）

基因型和表現型

島嶼種群

島嶼的概念最常用於競爭種群，將潛在解分為多個種群，各自獨立發展。島嶼間偶爾可以進行交互。

多元種群也可用於合作種群，類似多個團隊合作解決同一問題。

實際用途：多元種群與分佈式計算非常兼容，同步問題是分佈式計算中最困難的問題之一，但由於種群之間彼此獨立，不需要同步，因此很容易在並行系統上實現。

適應度函數

適應度函數用於評估種群並指定分數，函數必須提供一個可以相互比較的數字分數

計分通常是演化演算法的性能瓶頸

選擇 / 抽樣

「選擇」是從種群中挑選一個或多個潛在解的過程，也叫「抽樣」

截斷選擇

根據適應度對種群排序，然後按分數選取一定比例的個體作為育種種群。在育種種群取樣潛在解，來產生下一代。
image.png
由於要不斷排序，嚴重限制了演算法的並行能力

此外，育種種群只產生後代，而沒有加入下一代，因此可能沒有孩子達到或超過上一代的最優解。因此需要挑選「精英」直接複製到下一代。

聯賽選擇

通過一系列的輪數進行，獲勝者進入下一輪

第一輪隨機選兩個個體，之後每輪都由上一輪的勝者與一個新的隨機個體進行比較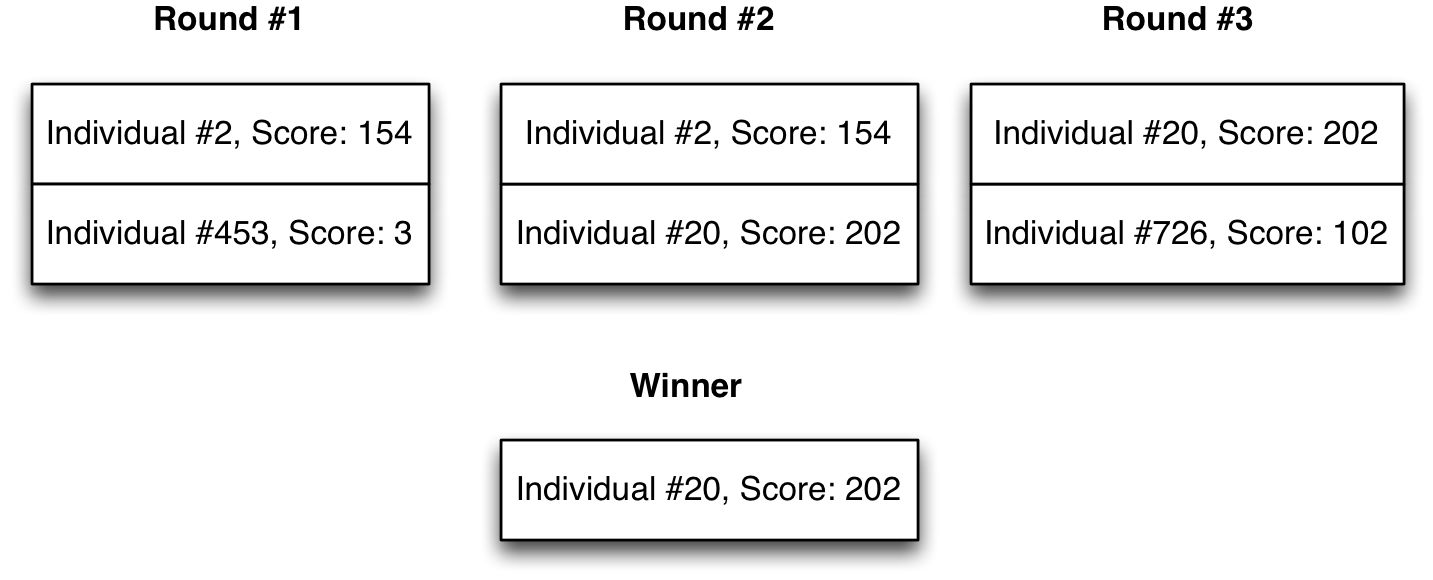
image.png

「反轉聯賽」指在種群中選擇不適應的個體

不需要排序，對並行處理非常有效

聯賽選擇還可以打破演化運算元常用的典型世代模型，就像人類一樣，每時每刻都有人出生，也有人死亡，世代的起止沒有明確的時刻

打破世代模型的具體做法：聯賽選擇兩個親本，生一個孩子，反轉聯賽選一個不適應的個體，將其「殺死」，由前面的孩子代替。不需要精英，因為最優解永遠不會被取代，反轉聯賽必不可能選到最優解。

選擇輪數

輪數作為超參數，一般通過反複試驗得出。

我通常設置種群數量 1000，輪數為 5

適應度比例選擇 / 輪盤賭選擇

個體佔據輪盤的一部分，得分越高，佔的越多，旋轉輪盤時被選到的幾率就越大。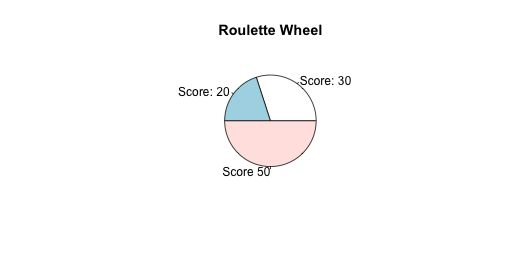
image.png
輪盤賭可以選到最差的個體，而截斷和聯賽不可能選到最差的。選擇最差的不一定是壞事，它可以增加基因的多樣性，最差的個體可能也會有一些優秀的基因

具體實現依然要進行排序或遍歷整個種群，很難並行運行

隨機遍歷抽樣

Stochastic Universal Sampling, SUS

選取單個隨機數，按照均勻的間隔選擇個體

如下圖，下面那條線，最左側的點就是生成的隨機數，之後每間隔 f/N 取一個個體

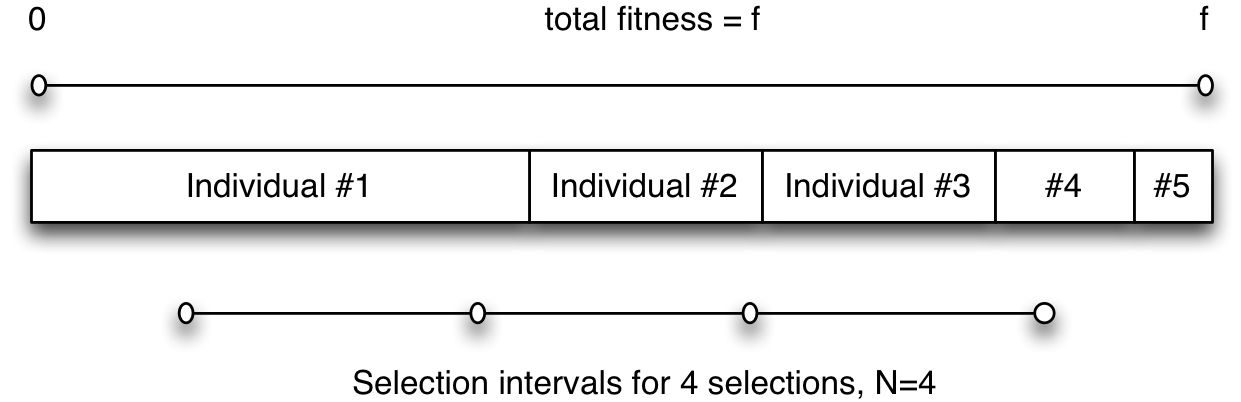
image.png
可能會多次選擇同一個個體

SUS 需要計算種群的總分數，也要排序

我該如何選擇？

我總是使用聯賽選擇，快速，可擴展。缺點在於非常弱的個體很早被淘汰，沒有辦法優化自身的基因，種群可能止步於已有的最高分數。