Processing #P5JS #CellularAutomaton #LifeGame

二維 CA 會引入額外的複雜度，每個細胞有更多的鄰居，同時也為更多的應用場景開啟了大門.

首先，我們需要一個二細胞維矩陣，而不是一行細胞

狀態依然是 0 或 1，代表「死」或「生」

現在我們有 9 個鄰居細胞

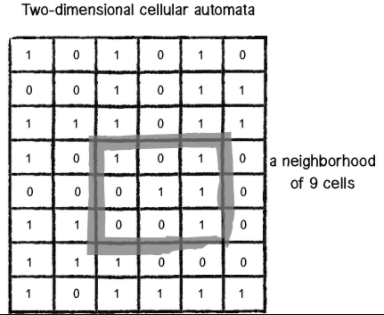
Pasted image 20210214231738.png

在只有 3 個鄰居時，狀態組合可以用一個 3 位的二進制數表示，是 8 種可能

現在有 9 個鄰居，有 512 種可能的狀態組合，分別定義規則是不可行的

規則

生命遊戲根據鄰居的一般特征制定了一套規則：

  1. 死亡：活著的細胞在一下情況下回變成死亡狀態:
    • 群體過剩：細胞有 4 個及以上的鄰居處於活著的狀態
    • 孤獨：活著的鄰居數少於等於 1 個
  2. 新生：處於死亡的細胞，如果周圍剛好有 3 個活著的鄰居，則會變為活著的狀態
  3. 靜止：其他情況
    • 保持活著：周圍有 2 個或 3 個活著的鄰居
    • 保持死亡：周圍活著的鄰居不等於 3

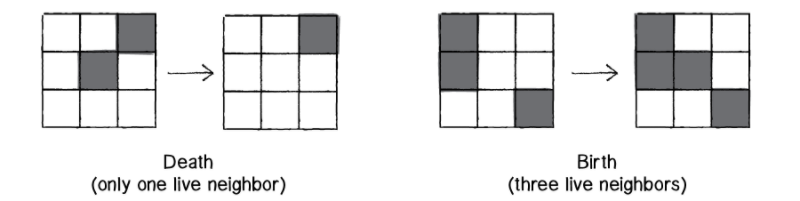
Pasted image 20210214232628.png

一些圖案

生命遊戲具有一個有趣的特性：某些初始圖案能帶來奇妙的結果:

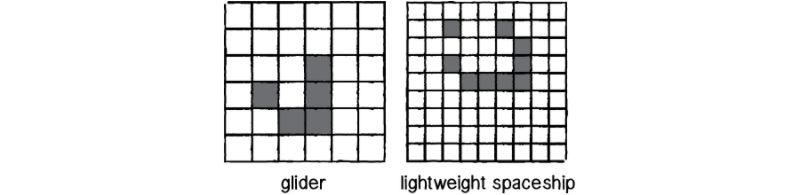
  • 以下圖案會保持靜止，不會發生任何改變
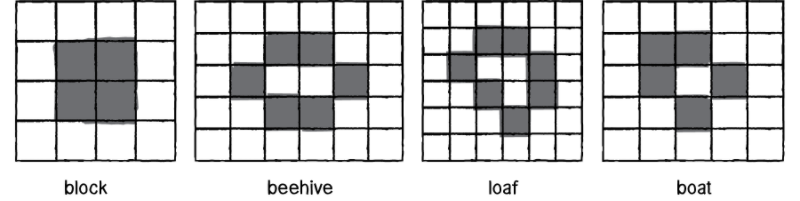
    Pasted image 20210214232756.png
  • 在兩個狀態之間交替出現
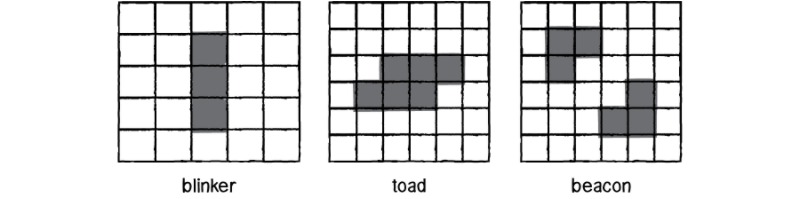
    Pasted image 20210214232848.png
  • 發生移動(移動是生死交替的結果，細胞本身沒有移動)，一般稱為「飛船」
    Pasted image 20210214232901.png

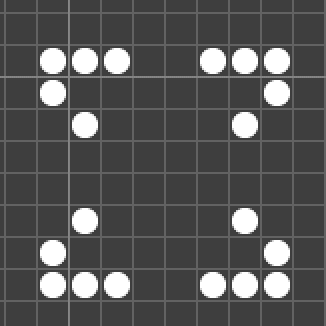image.png 四個「滑翔機」
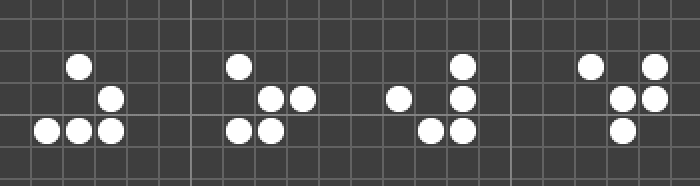image.png 滑翔機的四個階段

  • 需要大量迭代才能收斂的圖案稱為「瑪士撒拉 Methuselah」，下圖為一個簡單的瑪士撒拉，在收斂之前的壽命為 23314 次迭代

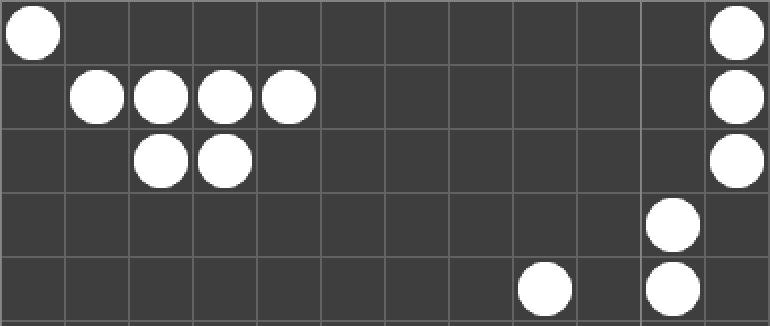
image.png


編寫生命遊戲

在生命遊戲中，所有規則都只涉及 “活著” 的細胞數量，因此引入一個鄰居計數器變數，每次發現一個”活著”的鄰居，就遞增這個變量，從而得到”活著”的鄰居的總數

傳統 CA 的變化

  1. 非矩形網格

Pasted image 20210215114242.png

  1. 概率性: CA 的規則不一定產生確定的結果
  2. 連續的: 細胞的狀態可以是 0~1 的浮點數
  3. 圖像處理: 大部分圖像處理算法和 CA 規則類似
  4. 歷史性: 我們記錄細胞的當前狀態和上一代狀態, 可以用數組存放更多的歷史狀態
  5. 移動細胞: 細胞的位置可以使不固定的, 可以在熒幕上移動
  6. 嵌套: 複雜系統還有一個特性, 即系統之間可以互相嵌套. 我們的現實世界就具有這樣的特性: 城市是由人組成的複雜系統, 人是由器官組成的複雜系統, 器官是由細胞組成的複雜系統…