8. Optimization Training

• Hill Climbing 爬山法
• Simulated Annealing 模擬退火
• Nelder Mead 演算法

  爬山法

在貪心隨機算法中，每次都隨機獲取一個長期記憶，無法通過微調來漸進優化

爬山法則在當前的記憶向量上進行優化，隨機初始化在一個「山腰」位置，每次朝著一個更高/更低的位置前進一步，最後到達一個局部最高點/最低點

最終的結果也許不是全局最優的（除非是一個非常簡單的模型，否則很難找到一個全局的最優解）

如果發現訓練陷入了某個區域，可以考慮再次隨機選取一個「山腰」

具體實現中有多重策略

模擬退火法

「退火」是冶金學的一個過程，將金屬加熱，然後緩慢冷卻。

模擬退火算法，從某個「高溫點」開始，此時長期記憶在一個很大的區間隨機取值。

隨著訓練過程的進行，溫度開始下降，長期記憶的變化範圍也跟著變小

模擬退火依然是「貪心」的，保存的還是已知的最優解

基於當前位置，考慮下一步的行動
隨機選擇一個「下一步」，如果效果更好，則移動到新位置
如果效果更差，則會根據概率決定是否移動（概率與「溫度」有關），溫度越高，移動的概率就越大

冷卻進度

用來描述迭代期間「溫度」下降的速度，初期較高，逐漸減小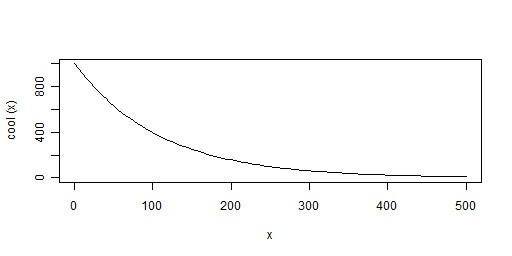

給定初始溫度和目標溫度（不能為 0），可以用下述公式計算：

退火概率

接受三個輸入：

• 當前誤差
• 前一步的誤差
• 當前溫度

溫度越高，P 越大

返回值在 (0, 1) 之間，返回 1 表示選擇更壞的結果的概率為 100%

將 P 和隨機生成的一個數字進行比較，若隨機數更大，則接受這個更壞的結果

Nelder-Mead 演算法

也叫 「下山單純性法」，「變形蟲法」

首先構造一個「單純形」（在碰撞檢測中有提到過），假設求解的問題是 N 維的，則該單純形就有 N+1 個頂點

單純形本質上是一組可能解的集合，算法總是保存著 N+1 個可能的解，隨著訓練進行，形狀會不斷改變。到訓練後期，這個單純形會變得很小，此時選擇表現最好的頂點作為解即可。

Nelder-Mead 演算法最初會假定一個解向量（可以隨機生成一個解），如果之前有進行過一次 Nelder-Mead 演算法，可以取其解作為初值，進一步優化。

初始的解向量會作為起始的單純形的一個頂點，因此還需要 N 個頂點，將初始向量的 N 個維度分別改變一定的量，即可得到餘下的 N 個頂點。

通常情況，初始單純形的各邊都是等長的。

以二維空間中的一個三頂點單純形為例：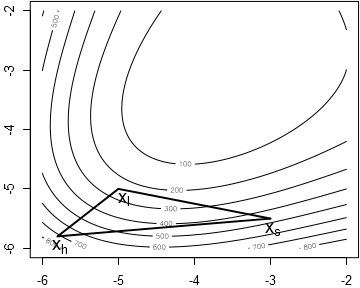

可以將頂點視為登山隊員，每個隊員都在尋找地圖上的最優點，演算法則是根據更好的兩個隊員，來把最差的隊員移動到更好的位置上。

演算法一次迭代包含以下步驟：

1. 找出最差，次差和最佳的頂點
2. 把最差的點向更好的一側「反射」
3. 反射成功，則擴張
4. 反射失敗，則收縮

比較古老的實現中會有一個「萎縮」的步驟，不過後來發現多此一舉

反射 Reflection

如圖所示，最差的點是 Xh，c 為 Xs 和 XI 的中點。Xh 要沿著虛線方向前進，這裡選取了一個很遠的目標點 Xr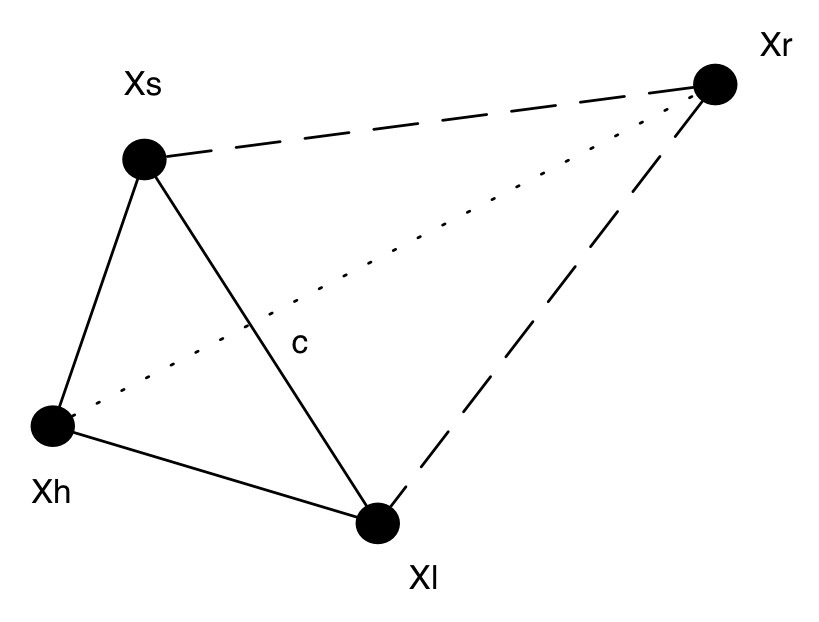

之後要對 Xr 進行評估，判斷其表現是否有進步

擴張 Expansion

隊員 Xh 發現移動到 Xr 效果更好，然後他貪了，想跑的更遠一些，於是他選擇走到 Xe 處。本次迭代結束。

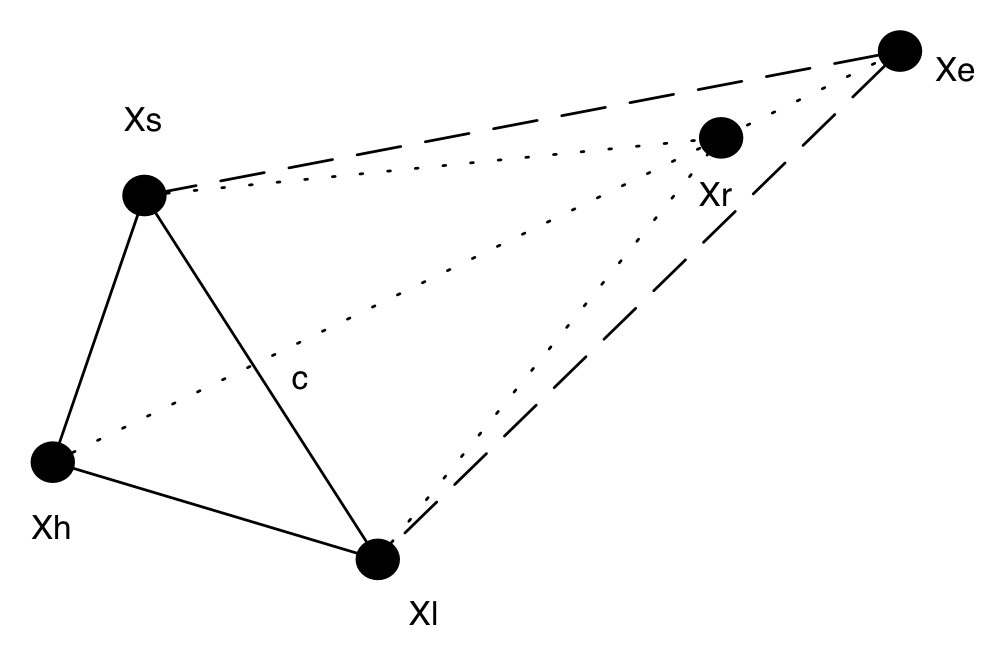
收縮 Contraction

發現跑到 Xr 效果並不如 Xh，所以更好的選擇雖然是向 Xs 和 XI 繼續靠攏，但移動不超過 C 點。本次迭代結束。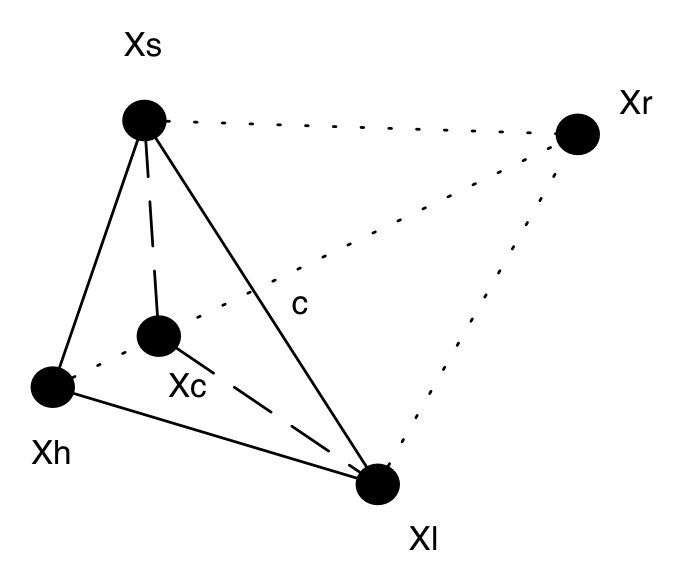

終止條件

對於這類迭代演算法，何時終止很重要，一般有 3 個獨立的判斷標準：

1. 迭代次數超過最大值
2. 結果足夠好
3. 各頂點距離足夠近

倘若頂點擠作一團，可以選擇將最佳頂點作為頂點之一，重新構造一個單純形，再運行一遍算法

Nelder-Mead 演算法每次迭代只需要重新評估一個頂點，因此效率較高。