Processing #P5JS #CellularAutomaton

本章將構建另一個複雜系統，但我們要簡化系統的組成元素：系統的元素不是物理世界的實體，而是最簡單的數字——位元（比特）。一個位元位稱為元胞，它的值（0 或 1）稱為狀態。使用這些簡單的元素能幫助我們深入理解複雜系統和其中的實現技術

元胞自動機是由「元胞」物件組成的系統，它具有以下特性:

• 元胞存在於網格中（任意維度）
• 每個元胞都有一個狀態，但可能出現的狀態數量是有限的，最簡單的情況就是 1 和 0（開和關，或者生和死）
• 每個元胞都有「鄰居」，定義鄰居的方式有多種，通常指鄰近的元胞

在元胞自動機領域，最有意義（且篇幅最長）的科學研究是 Stephen Wolfram 於 2002 年發表的著作 New Kind of Science，共計 1280 ⻚。該書宣告，CA 並不是一種簡單的遊戲，它和生物學，化學，物理學以及各個科學分支都密切相關

Wolfram 初等元胞自動機

Elementary Cellular Automaton，是一維的

CA 的三大要素:

• 網格: 一行細胞
• 狀態集: 0 和 1
• 鄰居: 左右的細胞

我們可以根據鄰居先前的狀態來計算細胞新的狀態:

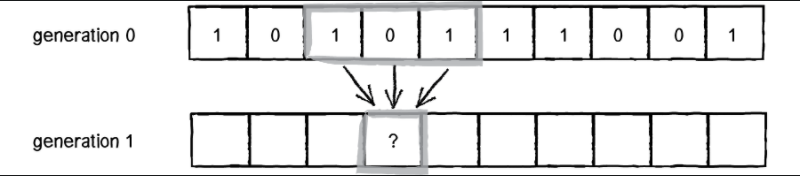
舉個簡單的例子，考慮只有一個元胞的自動機，時間步 時該元胞的狀態為整數 ，初始 。 設定規則 ，每執行一步，元胞的值都 +1，該 CA 執行的就是所謂的計數操作。 不過通常 CA 的狀態是有限的，我們假設一個元胞的狀態只有 0 和 1 兩種，規則改為 %5C%252#card=math&code=x_%7Bi%2B1%7D%3D%28x_i%20%2B%201%29%5C%252&id=zu48U)，這樣該元胞的行為是每步都在 0 和 1 之間進行切換。 這個簡單的例子中只有一個元胞，可以看作是零維的，接下來的內容都是圍繞一維 CA 的，二維的 CA 將在下一篇中進行介紹。 大多的 CA 都是確定性的，規則中不存在隨機要素，對於相同的初始狀態，產生的結果也是相同的。但也存在一些不確定的 CA，我們很快就可以看到。

Wolfram 發表了一系列論文，對一維 CA 進行了系統的研究。他確定了四類行為，每一類都比上一類更有趣。其中元胞排列在晶格中（可以視為一個一維數組），每個元胞附近有兩個元胞，晶格可以是有限的、無限的、或是環裝的。

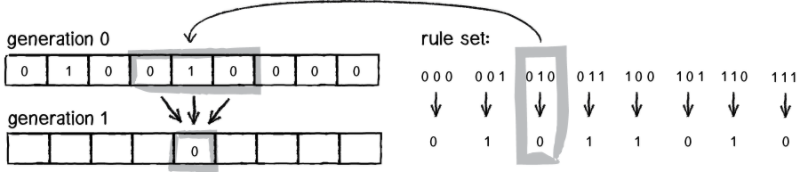
每個元胞依然是有 0 和 1 兩種狀態，決定一個元胞下一步的狀態的規則是基於其相鄰的兩個元胞的，也就是說一個三元胞組決定中間元胞下一步的值。

舉個例子：

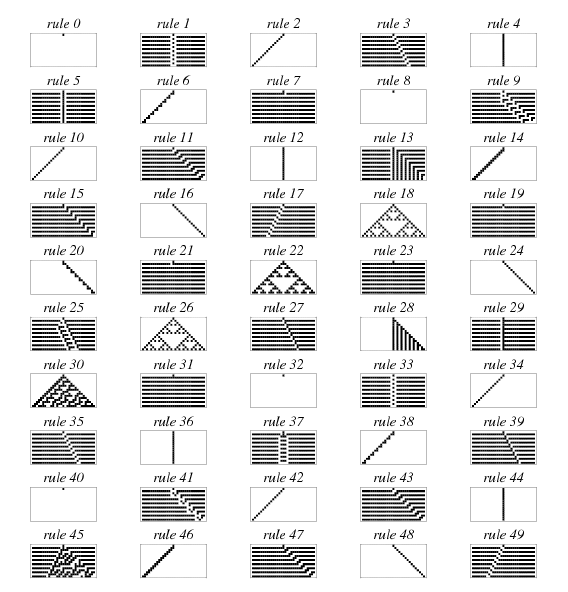
輸入狀態只有 8 種，因此規則最多有 種，將 next 作為一個二進位數字來對規則進行命名，上面的例子可以稱為「rule 50」

CA 的分類

Wolfram 將 256 種 CA 分為四類：

簡單

第一類是最簡單且最無趣的 CA，不論從何種狀態開始，它們都會迅速演變為一個穩定的模式，初始模式中的任何隨機性都會消失。比如「rule 0」，不論初始狀態如何，經過一步後，都是一個全 0 的空模式。

重複

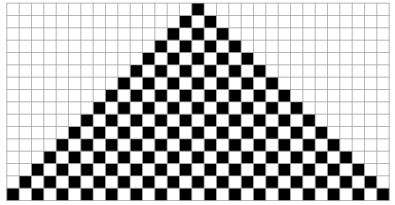
前面的「rule 50」屬於第二類，是具有嵌套結構的簡單模式，「rule 18」同樣如此，類似 Sierpiński 三角形的結構。但相對於後面兩類，依然是比較簡單的。

隨機

第三類 CA 則包含隨機性，幾乎所有的初始形態將會演變成一個偽隨機或混沌的形式。任何穩定的結構很快會被周圍的噪音破壞。在初始模式的局部變化有無限蔓延的傾向。「rule 30」如下圖所示

左側是是相同的圖樣，但右側產生了大小和位置都沒有規律的三角形，如果將取中間的一列取出來，很難將其與一般的隨機序列區分開，它可以通過許多隨機性的統計測試。

自然界中的 rule 30：

宇宙飛船

第四類 CA 更令人驚嘆，幾乎所有的初始模式都將演變成相互作用的複雜和有趣的結構，並且局部結構的形成能夠長時間存在。它們大部分是圖靈完備的（Wolfram 猜的），這意味著可以執行任何計算，也稱為普適性，其中最著名的是「rule 110」

嘗試從一個隨機序列開始，經歷 600 步后：

經過大約 100 步後，背景形成了一個簡單的重複模式，其中有一些長期存在的結構，一些是穩定的，它們看起來像垂直的線，另一些則在空間中進行平移，比如那些不同角度的斜綫，這些結構被稱為宇宙飛船 spaceships。

飛船間的碰撞會產生不同的結果，這取決於其類型和碰撞時所處的狀態。有些碰撞摧毀了兩艘船，一些只剩下了一艘船（未發生改變），還有一些碰撞產生了一艘或多艘新的的船。

在 「Rule110」中，這些碰撞是計算的基礎。如果您將飛船視為在空間中傳播的訊號，將碰撞視為邏輯運算的門，就可以看到 CA 執行着怎樣的運算。

普適性 Universality

這一節可以不看，只是簡單介紹下普適性是什麽以及一些相關的歷史。 關於圖靈機與可計算性的科普個人推薦 Crash Course 電腦科學中的相關影片 個人理解的話，說「Rule 110」具有普適性，就是說用它的那些飛船可以構造出各種邏輯門，從而執行任何運算和程式。

為了理解普適性，我們必須理解可計算性理論，它是關於計算模型及其計算內容的理論。

最通常的計算模型之一是圖靈機，它是由 Alan Turing 在 1936 年提出的一種抽象計算機。圖靈機是一個一維 CA，在兩個方向上都是無限的，並帶有一個讀寫頭。在任何時候，頭部都位於單個元胞上，它可以讀取該元胞的狀態（通常只有兩種），也可以向元胞中寫入新值。

此外，機器還有一個寄存器，用來記錄機器的狀態（有限個狀態之一）和一個規則錶。對於每個機器狀態和元胞狀態，該錶會指定一個操作，包括修改頭部所在的元胞，向左或向右移動一格。

圖靈機模擬了常見的計算機體系結構，對於在真實電腦上運行的給定程式，可以（至少在原則上）構造一個執行等效計算的圖靈機。

圖靈機可以描述一個可以被圖靈機計算的函數的集合，這些函數就是「圖靈可計算的 Turing Computable」。

說圖靈機器可以計算任何圖靈可計算函數是一個重言式：定義上來說沒毛病。但圖靈可計算性要更加有趣。

事實證明，任何人提出的任何一個合理的計算模型都是「圖靈完備的」；也就是說，它可以計算出與圖靈機器完全相同的函數集。其中一些模型，如 lamdba 運算元，與圖靈機非常不同，因此它們的等價性令人驚訝。

這一觀察結果產生了 Church-Turing 理論，該理論認為這些可計算性的定義包含了一些更基本的東西，獨立於任何特定的計算模型。

「Rule 110」CA 也是一種計算模型，它以簡單著稱，它也是圖靈完備的，這也支持了 Church-Turing 的理論。

基於 P5.JS 實現一維 CA

原程式碼：https://github.com/IsumiAlice/Cellular-Automaton-Ground

處理邊界

如何處理沒有左右鄰居的邊界細胞? 有如下三種方案:

1. 讓邊界的狀態保持常量 0 或 1
2. 邊界環繞，變成一個環
3. 為邊界創建新的規則，會引入許多額外程式碼，收益卻很少

採用第一種方案，實現也很簡單，只需要讓循環從下標 1 開始，並提前一個元素結束

雙數組

我們不能直接覆蓋數組的值，因此需要兩個數組

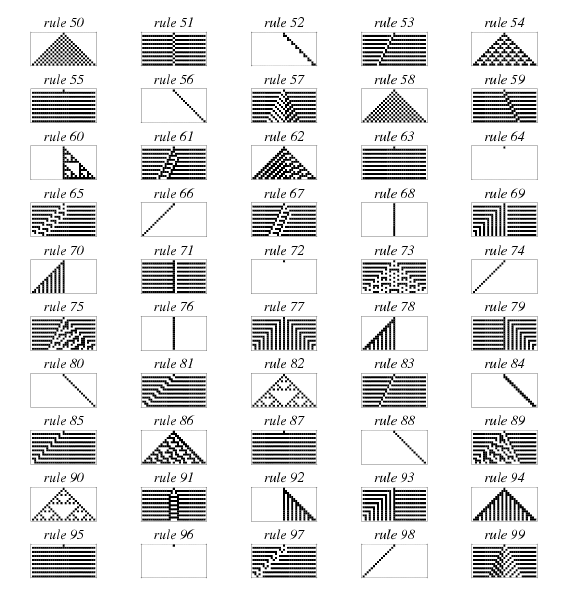
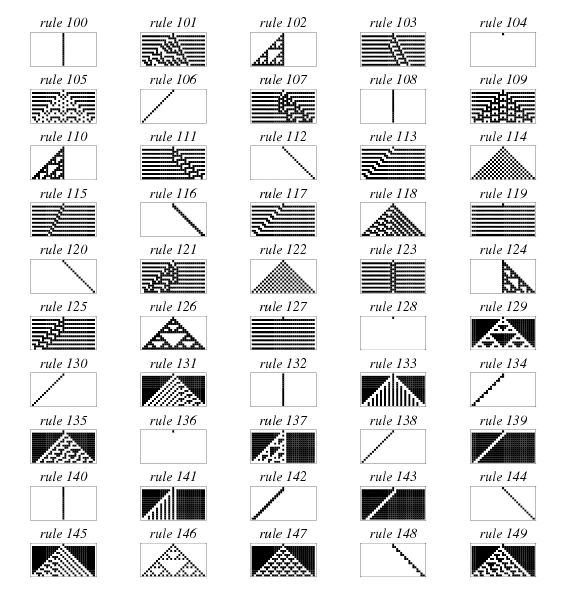
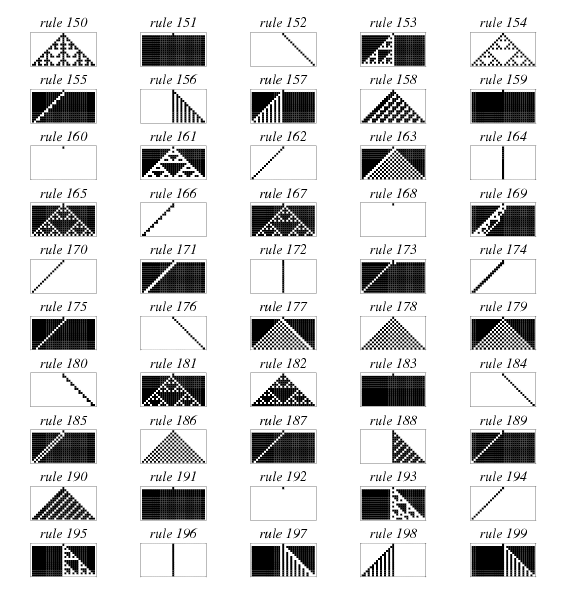
256 種 ECA

https://mathworld.wolfram.com/ElementaryCellularAutomaton.html