章节8 正则化

过拟合问题(Over-fitting)

• 线性回归中的表现
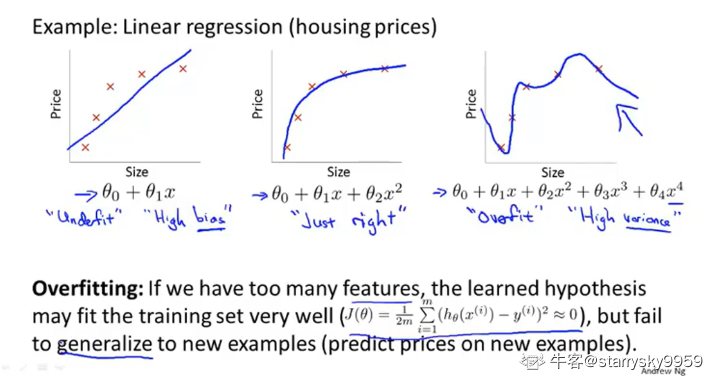
  下图中的三张分别展示了用不同数量参数拟合房价问题的情况 | | 左边 | 中间 | 右边 | | —- | —- | —- | —- | | 特征数量 | 少 | 适中 | 多 | | 拟合情况 | 欠拟合 | 恰当 | 过拟合 | | 表现总结 | 高偏差 | 准确 | 高方差 |

过拟合: 用了过多特征, 虽然假设函数对于当前数据集的描述十分准确, 甚至可以说是几乎经过了所有样本点, 代价函数 %5Capprox0#card=math&code=J%28%5Ctheta%29%5Capprox0) , 但是显然这个假设函数并不能很好地泛化到新的样本. 通常来说是因为特征太多而样本太少而导致的

• 逻辑回归中的表现
  简单看一下上述三种情况在逻辑回归中的表现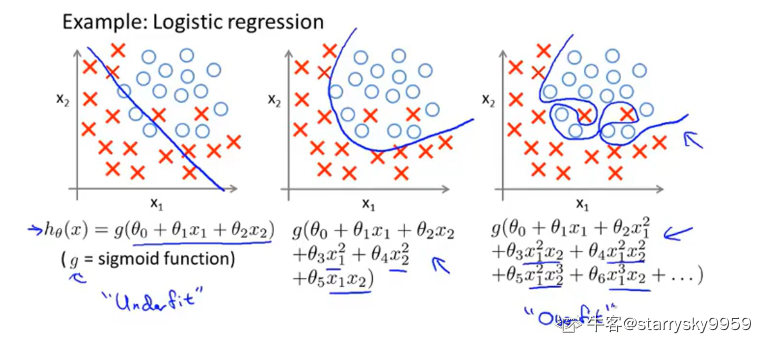
  

• 处理过拟合问题

  1. 减少特征数量
     可以人工选择剔除不重要的特征, 也可以用算法来自动选择保留哪些特征.
     当然, 减少特征的同时也就意味着舍弃了一部分描述问题的信息.
  2. 正则化(Regularization)
     保留全部的特征, 但减小数值的量级
     可以回想一下线性代数中矩阵的正则化

代价函数的正则化

先通过一个例子来理解一下正则化背后的思想.

首先我们优化目标: 最小化均方误差代价函数 #card=math&code=J%28%5Ctheta%29)
既然只包含 3 个特征的二次函数的拟合效果不错, 那么我们来简单修改一下 #card=math&code=J%28%5Ctheta%29), 引入一种惩罚机制来降低新增的两个参数 和 对于包含 5 个特征的四次函数的影响.
简言之, 就是使这个四次函数的高次项参数尽可能小, 从而使它更像原来的二次函数

%3D%5Cmin%7B%5Ctheta%7D%7B%5Cfrac%7B1%7D%7B2m%7D%5Csum%7Bi%3D1%7D%5E%7Bm%7D(h%5Ctheta(x%5E%7B(i)%7D)-y%5E%7B(i)%7D)%5E2%2B1000%5Ctheta_3%5E2%2B1000%5Ctheta_4%5E2%7D#card=math&code=J%28%5Ctheta%29%3D%5Cmin%7B%5Ctheta%7D%7B%5Cfrac%7B1%7D%7B2m%7D%5Csum%7Bi%3D1%7D%5E%7Bm%7D%28h%5Ctheta%28x%5E%7B%28i%29%7D%29-y%5E%7B%28i%29%7D%29%5E2%2B1000%5Ctheta_3%5E2%2B1000%5Ctheta_4%5E2%7D)

由于有了新增的两项 和 , 为了得到尽可能小的 #card=math&code=J%28%5Ctheta%29), 和 也需要尽可能小. 我们想要的效果就达到了

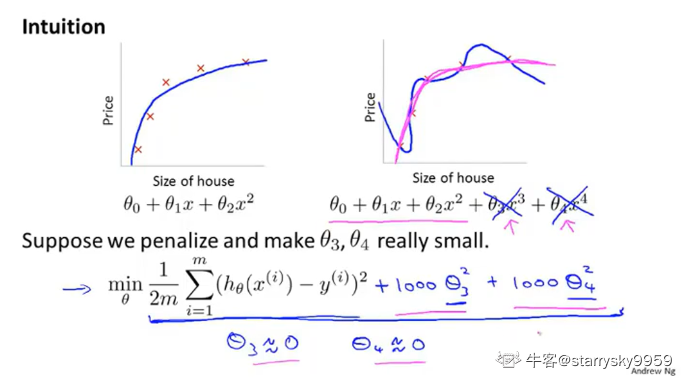
从上述例子上, 我们可以体会到正则化背后的思想: 较小的参数数值意味着较简单的假设函数模型以及较少的过拟合

而实际中我们所做的, 就是对所有参数项都加上正则项来缩小所有参数

被称为正则化参数, 用于控制原代价函数项和正则项这两个之间权重的取舍
过小意味可能出现过拟合; 而 过大意味着可能出现欠拟合

线性回归的正则化

用正则化优化之前学过的的梯度下降和正规矩阵法

通常对于第一项 不做正则化处理

• 推广到梯度下降
  现在我们对进行了正则化的代价函数 #card=math&code=J%28%5Ctheta%29) 使用梯度下降, 直观的效果就是每次更新都让 先缩小一些, 然后进行梯度下降

• 推广到正规矩阵
  添加一个 维的对角矩阵(但第一行第一列也为0)作为正则项, 同时这可以保证括号内的矩阵是可逆的

逻辑回归的正则化

与线性回归同理, 不过注意两者 #card=math&code=h_%5Ctheta%28x%29) 含义的不同