章节7 Logistic 回归

分类(Classification)

• 二元(本节讨论)

  
  0 表示负类(Negative Class)
  1 表示正类(Positive Class)

• 多分类问题(后续详细讨论)

  

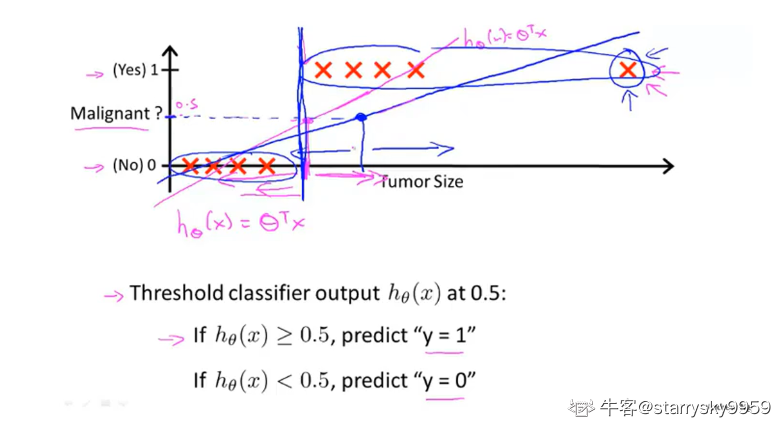
如果将线性回归应用于分类问题,如设置阈值对结果进行分类,
当增加新的样本后, 拟合曲线发现变化可能导致原来的阈值不再适用
通常, 即使所有训练样本的标签都是 , 算法的输出值也会远大于1或远小于0

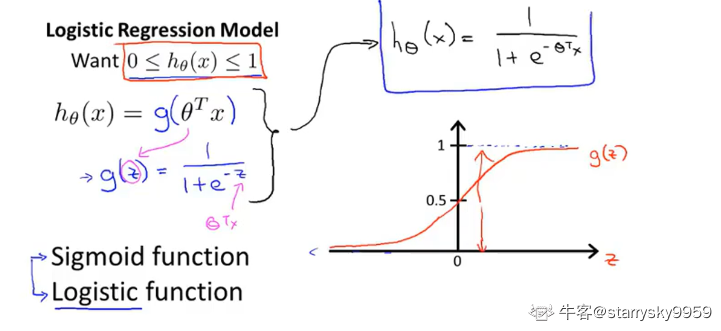
逻辑回归(Logistic regression)

sigmoid/logistic function, 保证输出值 %5Cin%5B0%2C1%5D#card=math&code=h_%5Ctheta%28x%29%5Cin%5B0%2C1%5D):

%3D%5Cfrac%7B1%7D%7B1%20%2B%20e%5E%7B-z%7D%7D#card=math&code=g%28z%29%3D%5Cfrac%7B1%7D%7B1%20%2B%20e%5E%7B-z%7D%7D)

假设陈述

假设函数 #card=math&code=h_%5Ctheta%28x%29) 表示对于参数矩阵 , 当输入的特征向量为 时, 输出结果 的概率

决策界限(Decision boundary)

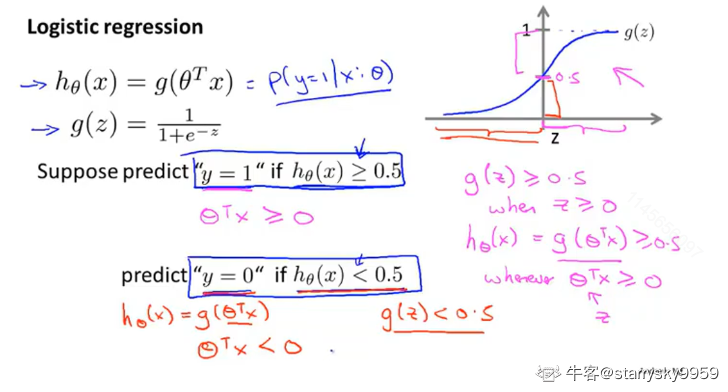
既然假设函数 #card=math&code=h_%5Ctheta%28x%29) 表示概率, 那么我们可以通过这个输出对于最终的分类结果这样界定

%20%5Cgeq%200.5#card=math&code=h%5Ctheta%28x%29%20%5Cgeq%200.5) , 则
%20%3C%200.5#card=math&code=h_%5Ctheta%28x%29%20%3C%200.5) , 则

又因为 %20%3D%20g(%5Ctheta%5ETx)#card=math&code=h_%5Ctheta%28x%29%20%3D%20g%28%5Ctheta%5ETx%29), 且 #card=math&code=g%28z%29) 的函数图像我们已知,那么

• 线性的决策边界
  对于下图的例子,现在我们先假定已经选好参数 , 根据上述的推导关系, 我们可以很快知道
  代表 的范围和坐标系中满足条件 的区域是一样的
  这条直线就是图中两个簇的决策界限(Decision boundary)
  决策界限是假设函数的一个属性, 决定于其参数 而非数据集,
  后续将讨论如何通过数据集拟合参数 , 而一旦参数确定下来, 也就有了完全确定的决策界限,
  实际上我们并不需要通过绘制数据集来确定决策界限
  

• 非线性的决策边界
  通过添加高阶多项式, 我们可以得到更加复杂的决策边界
  

代价函数(Cost function)

复杂的非线性函数sigmoid使代价函数 #card=math&code=J%28%5Ctheta%29) 成为一个非凸函数(Non-convex function), 这样就不能使用梯度下降算法

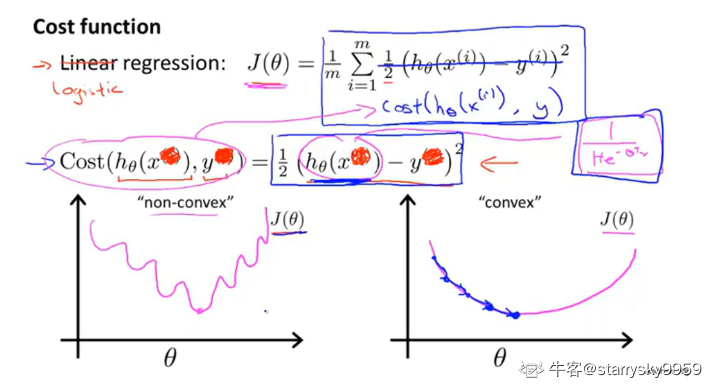
%2C%20y)#card=math&code=Cost%28h%5Ctheta%28x%29%2C%20y%29) 函数可以理解为惩罚函数
下面这张图很直观地体现了它的作用(此时正确答案 , 的情况同理)
观察 %3D1%5Crightarrow0#card=math&code=h%5Ctheta%28x%29%3D1%5Crightarrow0) 的过程, 可以发现, 随着 预测值#card=math&code=h_%5Ctheta%28x%29) 的值偏离正确答案 , 惩罚函数 Cost 的值也从 , 以此来迫使预测值向正确值修正

简化代价函数和梯度下降

首先来化简一下代价函数的写法, 避免分类讨论的麻烦

%2C%20y)%3D-ylog(h%5Ctheta(x))%20-%20(1-y)log(1-h%5Ctheta(x))#card=math&code=Cost%28h%5Ctheta%28x%29%2C%20y%29%3D-ylog%28h%5Ctheta%28x%29%29%20-%20%281-y%29log%281-h%5Ctheta%28x%29%29)
%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%7Bi%3D1%7D%5E%7Bm%7D%7BCost(h%5Ctheta(x_i)%2C%20y_i)%7D#card=math&code=J%28%5Ctheta%29%3D%5Cfrac%7B1%7D%7Bm%7D%5Csum%7Bi%3D1%7D%5E%7Bm%7D%7BCost%28h%5Ctheta%28x_i%29%2C%20y_i%29%7D)
)%20%2B%20(1-y_i)log(1-h%5Ctheta(xi))%7D)#card=math&code=%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%5C%20%3D-%5Cfrac%7B1%7D%7Bm%7D%28%5Csum%7Bi%3D1%7D%5E%7Bm%7D%7Byilog%28h%5Ctheta%28xi%29%29%20%2B%20%281-y_i%29log%281-h%5Ctheta%28x_i%29%29%7D%29)

接下里, 为了拟合参数 , 需要求解 %7D#card=math&code=%5Cmin_%7B%5Ctheta%7D%7BJ%28%5Ctheta%29%7D), 方法依然是梯度下降

其中 %20%3D%20%5Csum%7Bi%3D1%7D%5E%7Bm%7D%7B(h%5Ctheta(xj%5E%7B(i)%7D)-y%5E%7B(i)%7D)x_j%5E%7B(i)%7D%7D#card=math&code=%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%5Ctheta_j%7DJ%28%5Ctheta%29%20%3D%20%5Csum%7Bi%3D1%7D%5E%7Bm%7D%7B%28h%5Ctheta%28x_j%5E%7B%28i%29%7D%29-y%5E%7B%28i%29%7D%29x_j%5E%7B%28i%29%7D%7D)
虽然参数更新的规则一样, 和线性回归中的不同的是
在线性回归中, %3D%5Ctheta%5ETx#card=math&code=h%5Ctheta%28x%29%3D%5Ctheta%5ETx)
在逻辑回归中, %3D%5Cfrac%7B1%7D%7B1%2Be%5E%7B-%5Ctheta%5ETx%7D%7D#card=math&code=h_%5Ctheta%28x%29%3D%5Cfrac%7B1%7D%7B1%2Be%5E%7B-%5Ctheta%5ETx%7D%7D)

高级优化算法

• Conjugate gradient
• 共轭梯度法BFGS, L-BFGS

都采用了线搜索算法,自动尝试不同的学习率
不需要手动选择学习率 , 且通常快于梯度下降

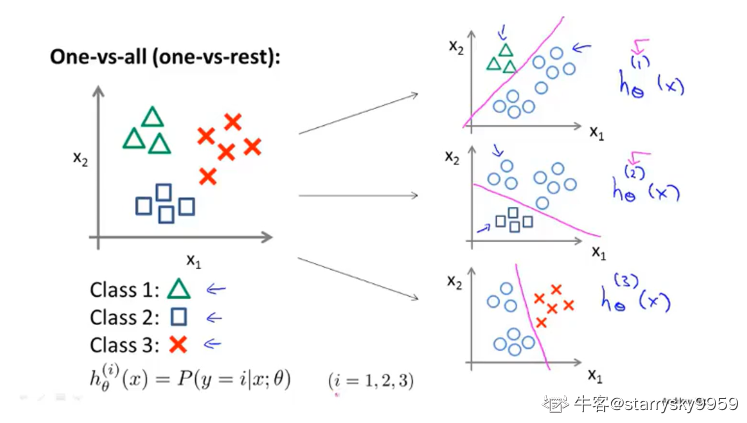
多元分类: 一对多(one-vs-all/rest)

如下图例子, 我们将一个三元分类问题转化为 3 个独立的二元分类问题
对于每一个类 , 训练一个分类器来预测数据集中各个样本 的概率
在 3 个分类器中依次输入样本 的值, 选择 %7D(x)%7D#card=math&code=%5Cmax%7Bi%7D%7Bh%5Ctheta%5E%7B%28i%29%7D%28x%29%7D) 对应的第 类作为答案, 即概率最高的那一类