进行第一次神经网络搭建, 训练的实战
任务: 用数据点拟合关系曲线

实现过程

  1. 导入模块

导入一下要用到各个模块, Variable 在我用的版本中已经弃用了, 和 tensor 一致.

  1. import torch
  2. from torch.autograd import Variable # 当前版本已经不需要了
  3. import torch.nn.functional as F     # 激励函数
  4. import matplotlib.pyplot as plt     # 画图工具
  1. 生成原始数据

linspace(-1, 1, 100) 用于生成从 -1 到 1 之间 100 个 均匀分布 的数据
因为 torch 的特性， 我们用 unsqueeze 方法将这一组数据变成矩阵
我们的目标函数是 关系拟合(回归) - 图1, 当然要在其基础上用随机函数加上一些 噪点 

  1. # 造数据
  2. # x 轴数据(tensor) shape = (100, 1)
  3. # 把数组变为矩阵, torch 只能处理二维的数据
  4. x = torch.unsqueeze(torch.linspace(-1, 1, 100), dim= 1)
  5. # y 轴数据(tensor) shape = (100, 1)
  6. # y = x^2 + 噪声
  7. y = x.pow(2) + 0.2*torch.rand(x.size())
  1. 画出散点图

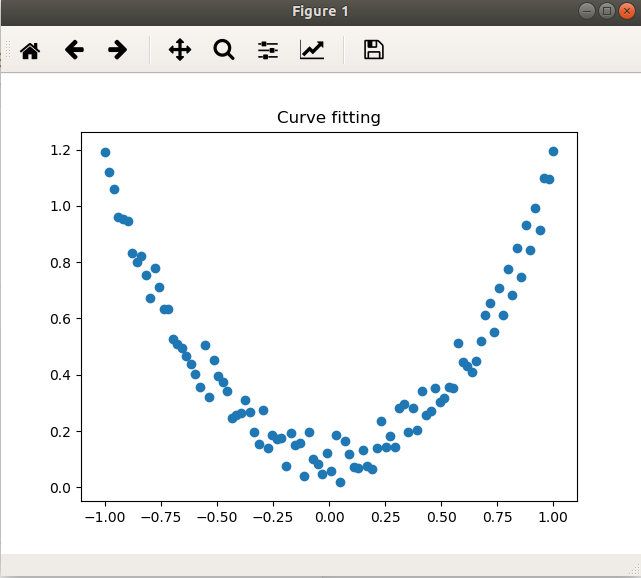
先画出散点图, 对前一步生成的数据点进行可视化

  1. plt.title("Curve fitting")
  2. # 绘制散点图
  3. # 或者 plt.plot(x.numpy(), y.numpy(), "o")
  4. plt.scatter(x.numpy(), y.numpy())
  5. plt.show()

效果如下图

图片.png

  1. 搭建神经网络

搭建网络前, 首先要继承 torch.nn.Module 这个官方的模块. torch.nn 是 torch 提供的 神经网络工具箱, 而 Module 是其中的 核心模块 , 它是一个抽象的概念, 既可以表示神经网络中的一层, 可以表示包含多层的神经网络.(此处参考陈云老师的《深度学习框架PyTorch: 入门与实践》) 因此在搭建网络前先继承这一父类可以帮助我们实现很多基础功能.以及在编写 __init__ 方法是时, 首先写上super(Net, self).__init__(), 这也是官方步骤. 然后就可以定义我们自己的网络了.
用 torch.nn.Linear 定义我们的 隐藏层 (本例中只用了 1 层) hidden 和 输出层 predict , 两个参数分别表示 输入特征 和 输出特征 的数量, 即定义了一个用于描述两层神经元之间映射关系的参数矩阵关系拟合(回归) - 图3, 输入特征,输出特征的数量描述了矩阵的大小.

然后定义 前向传播算法 的实现. 对隐藏层用 relu 激活函数, 对输出层就不再用激活函数. 因为通常来说最终结果的范围会在关系拟合(回归) - 图4之间, 用激活函数反而会限制答案的范围, 在本例中也适用. Linear 类已经实现了装有方法 __call__() , 所以实例 hidden 和 predict 可以像方法一样使用, Net 类也有性质, 查看 Linear 类的源码可以发现, 它和我们自己编写的 Net 类一样都继承自 Moudle
显然, 输入特征只有x轴坐标, 输出只有y轴坐标, 隐藏层神经元的数量可以自己定, 跟着莫烦老师一起用 10 个吧. 后续可以自己调参看看效果.
关于参数的 初始化 , 这一点 torch 已经帮我们做好了, 不用担心, 好像用的是 均匀分布(uniform distribution) , 有待考证. 

  1. # 定义我的神经网络
  2. class Net(torch.nn.Module): # 继承 torch 的 Module 模块
  3.     def __init__(self, nFeature, nHidden, nOutput):
  4.         # 继承父类的__init__ 的功能, 官方步骤
  5.         super(Net, self).__init__()
  6.         # 定义每层的形式
  7.         self.hidden = torch.nn.Linear(nFeature, nHidden)    # 隐藏层线性输出
  8.         self.predict = torch.nn.Linear(nHidden, nOutput)    # 输出层线性输出
  10.     # 前向传播
  11.     def forward(self, x):
  12.         x = F.relu(self.hidden(x))
  13.         x = self.predict(x)
  14.         return x
  16. net = Net(1, 10, 1)
  17. print(net)

一下便是输出结果, 可以大致一窥我们的神经网络的架构

  1. Net(
  2.   (hidden): Linear(in_features=1, out_features=10, bias=True)
  3.   (predict): Linear(in_features=10, out_features=1, bias=True)
  4. )
  1. 选择代价函数和优化方法

这里选择了随机梯度下降法, 学习率取 0.2, 代价函数的计算方法选择均方差, 即关系拟合(回归) - 图5

  1. # 准备训练网络
  2. # 优化器, 采用随机梯度下降法
  3. optimizer = torch.optim.SGD(net.parameters(), lr= 0.2)
  4. # 预测值和真实值的误差计算公式, 采用均方差
  5. lossFunc = torch.nn.MSELoss()
  1. 训练网络

计算预测值, 计算误差, 误差的反向传播(记得清零), 更新参数. 整一套神经网络学习的流程, 非常标准. 这里我们先迭代 100 次.

  1. for i in range(100):
  2.     # 给 net 训练数据 x, 输出预测值
  3.     prediction = net(x)
  4.     # 计算误差
  5.     loss = lossFunc(prediction, y)
  6.     # 清空上一步的残留更新参数值
  7.     optimizer.zero_grad()
  8.     # 误差反向传播, 计算参数更新值
  9.     loss.backward()
  10.     # 将参数更新值加到 net 的参数上
  11.     optimizer.step()
  1. 拟合曲线的可视化

完成前 6 步之后我们的神经网络就已经训练好了, 可以直接输出每次循环中的 prediction 与样本的因变量 y 进行对比, 或者输出 loss 来查看偏差值. 当然这种效果很难让人接受. 因此我们还需要 matplotlib 来帮助我们实现可视化
每迭代 5 次就用 predict 拟合一次曲线查看学习效果

  1.     if (i%5 ==0):
  2.         # 清除活动轴
  3.         plt.cla()
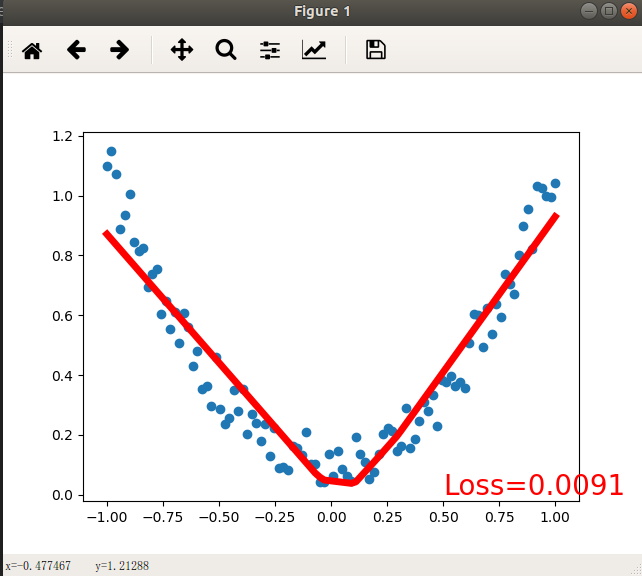
  4.         # 绘制原始数据散点图
  5.         plt.scatter(x.data.numpy(), y.data.numpy())
  6.         # 绘制拟合曲线
  7.         plt.plot(x.data.numpy(), prediction.data.numpy(), "r", lw=5)
  8.         # 打印误差
  9.         plt.text(0.5, 0.0, "Loss={:.4f}".format(loss.data), fontdict={"size": 20, "color": "red"})
  10.         plt.pause(0.15)
  11.         print(prediction)
  1. 最终效果

图片.png

总结

总的来说整个实现过程真的非常方便, 传递过程中的矩阵运算等细节不需要去管, 之前学的梯度检测也没有用上, 毕竟 PyTorch 肯定已经实现好了正确的反向传播. 而自己更多地是关注流程控制,参数选择以及 可视化 这种辅助工作上.

关系拟合(回归).py