在解决过拟合问题时，虽然简化模型和增大数据集是有效的方法，但是实际中并不常用，简化模型意味着有些特征被丢弃，增大数据集面临数据获取难的问题。权重衰减（weight decay）是一种更为常用的方法。
    权重衰减等价于 L2 范数正则化（regularization），教程中这样说，那么本节的内容可以参考吴恩达机器学习中关于正则化的部分。但是我不知道什么 L2 范数，先学一下这个新概念。
    关于 L2 范数参考链接：https://www.jianshu.com/p/4bad38fe07e6
    理论知识看教程复习即可。重点用代码实现看一下正则化的效果。

    • 生成数据集

    原始数据的函数关系为，p 表示特征向量的维数：
    3.12 权重衰减 - 图1
    为了制造过拟合的现象，减少训练集的大小，增加特征的数量。

    1. # 生成数据集
    2. elem_type = torch.float
    3. train_size = 20
    4. test_size = 100
    5. feature_size = 200
    6. true_w = torch.ones((feature_size, 1)) * 0.01
    7. true_b = 0.05
    8. features = torch.randn((train_size + test_size, feature_size))
    9. labels = torch.mm(features, true_w) + true_b
    10. labels += torch.normal(0, 0.01, labels.size(), dtype=elem_type)
    • 训练模型

    与前一节的函数类似，但是这次加上 wd 表示 L2 范数惩罚项的系数3.12 权重衰减 - 图2

    1. def fit_and_plot(train_features, train_labels, test_features, test_labels, wd):
    2.     """
    3.     训练模型并可视化训练结果和测试结果.
    4.     Args:
    5.         train_features: 训练集的特征
    6.         train_labels: 训练集的标签
    7.         test_features: 测试集的特征
    8.         test_labels: 测试集的标签
    9.         wd:
    10.     Returns:
    11.         无
    12.     Raises:
    13.         无
    14.     """
    15.     # 训练准备
    16.     iterate_num = 100
    17.     loss_func = torch.nn.MSELoss()
    18.     net = torch.nn.Linear(train_features.shape[-1], 1)
    19.     nn.init.normal_(net.weight, mean=0, std=1)
    20.     nn.init.normal_(net.bias, mean=0, std=1)
    21.     # PyTorch 默认对权重和偏差同时衰减, 这里只让权重衰减
    22.     optimizer_w = torch.optim.SGD(params=[net.weight], lr=0.01, weight_decay=wd)
    23.     optimizer_b = torch.optim.SGD(params=[net.bias], lr=0.01)
    24.     batch_size = min(10, train_labels.shape[0])
    25.     train_set = torch_data.TensorDataset(train_features, train_labels)
    26.     train_set_iter = torch_data.DataLoader(train_set, batch_size, shuffle=True)
    27.     # 存放学习后的误差数据点
    28.     train_lose_array, test_lose_array = [], []
    30.     for i in range(iterate_num):
    31.         for x, y in train_set_iter:
    32.             y_output = net(x)
    33.             current_lose = loss_func(y_output, y.view(y_output.size()))
    34.             optimizer_w.zero_grad()
    35.             optimizer_b.zero_grad()
    36.             current_lose.backward()
    37.             optimizer_w.step()
    38.             optimizer_b.step()
    39.         train_lose_array.append(loss_func(net(train_features), train_labels).mean().item())
    40.         test_lose_array.append(loss_func(net(test_features), test_labels).mean().item())
    41.         print("第{0}次迭代后, 训练误差={1:.4f}, 泛化误差={2:.4f}".format(
    42.               i + 1, train_lose_array[-1], test_lose_array[-1]))
    43.     print("矩阵范数={0}".format(net.weight.data.norm().item()))
    44.     d2lzh_pytorch.semilogy(range(1, iterate_num + 1), train_lose_array, 'epochs', 'loss',
    45.                            range(1, iterate_num + 1), test_lose_array, ['train', 'test'])
    • 效果展示

    先看一下不加权重衰减的表现，即 惩罚项系数 wd=0 

    1. # 无权重衰减
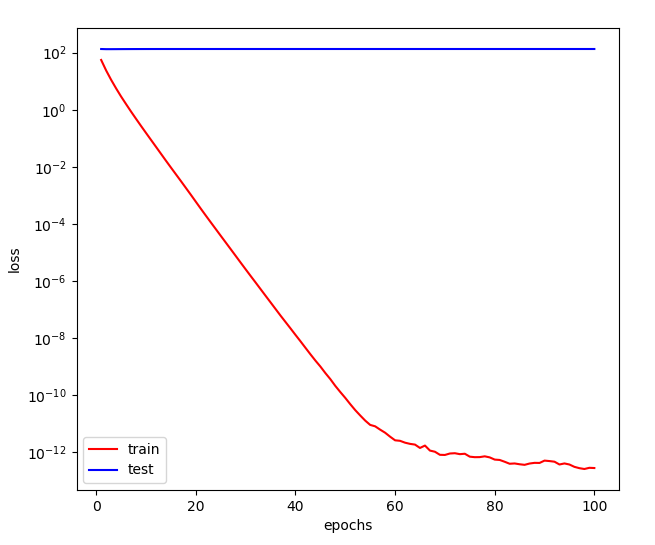
    2. fit_and_plot(features[:train_size, :], labels[:train_size],
    3.              features[train_size:, :], labels[train_size:],
    4.              wd=0)

    尽管训练误差近似为 0，但泛化误差高居不下。

    1. 第100次迭代后, 训练误差=0.0000, 泛化误差=134.0383
    2. 矩阵范数=12.42329216003418

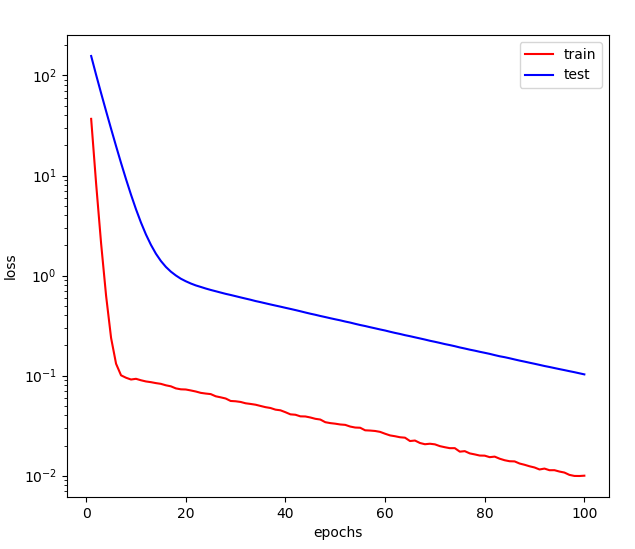
    图片.png
    再来看一下加上权重衰减后的效果，

    1. # 加上权重衰减
    2. fit_and_plot(features[:train_size, :], labels[:train_size],
    3.              features[train_size:, :], labels[train_size:],
    4.              wd=10)

    可以看到，泛化误差已经大大降低了，最终得到的矩阵范数也比较小。

    1. 第100次迭代后, 训练误差=0.0100, 泛化误差=0.1028
    2. 矩阵范数=0.07206203788518906

    图片.png
    3.12.2 高维线性回归实验.py