先只利用Tensor和autograd来实现一个线性回归的训练，先感受一下不用框架的工作量。
体验一下早期研究者的生活。3.2 线性回归的从零开始实现 - 图1

3.2.1 生成数据集和可视化

我们先设定好真实的模型参数3.2 线性回归的从零开始实现 - 图2以及服从 (0, 0.01) 正态分布的噪点3.2 线性回归的从零开始实现 - 图3(想到了CV中的高斯噪声)，显然标签3.2 线性回归的从零开始实现 - 图4满足一下公式
3.2 线性回归的从零开始实现 - 图5

  1. # 生成数据集
  2. # 统一类型
  3. elem_type = torch.float32
  4. # 特征个数
  5. feature_size = 2
  6. # 样本数量
  7. example_size = 1000
  8. # 真实的模型参数 (w, b)
  9. true_w = torch.tensor([[2, -3.4]]).t()
  10. true_b = torch.tensor(4.2)
  11. print(true_w, true_b)
  12. # 输入特征
  13. features = torch.randn(example_size, feature_size, dtype=elem_type)
  14. # 标签, 需要加上正态分布的噪点
  15. labels = torch.mm(features, true_w) + true_b
  16. labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=elem_type)
  17. print(features[0], labels[0])
  19. # 可视化
  20. # 设置图片大小
  21. base.set_figsize((10, 10))
  22. plt.scatter(features[:, 0], labels, s=5)
  23. plt.show()

运行结果

  1. tensor([[ 2.0000],
  2.         [-3.4000]]) tensor(4.2000)
  3. tensor([ 0.5475, -2.4344]) tensor([13.5706])

自己动手计算一下，数据生成无误。
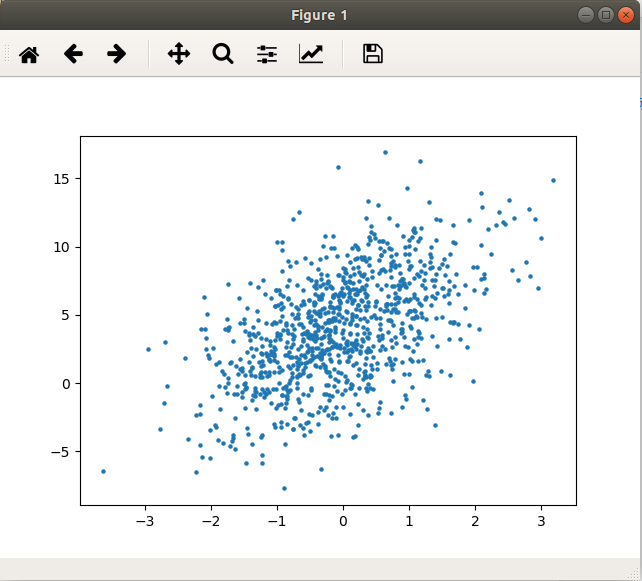
以下是取了3.2 线性回归的从零开始实现 - 图6,3.2 线性回归的从零开始实现 - 图7作为横纵轴来，大致可以看出两者的线性关系
图片.png
把作者提供的 d2lzh_pytorch模块放到可以搜寻到的路径下， 或者通过 sys.append() 来添加也可，这个包帮助我们实现了一些基础功能。

3.2.2 读取数据

用于小批量随机梯度下降算法中选取样本。

  1. # 已在 d2lzh_pytorch 包中的 data_iter 实现
  2. def data_iter(batch_size, features, labels):
  3.     """
  4.     从训练集中每次返回指定数量的随机序列样本.
  5.     Args:
  6.         batch_size: 返回的随机序列样本大小
  7.         features: 训练集的输入特征
  8.         labels: 训练集的标签
  9.     Returns:
  10.         随机序列样本, 大小为 batchSize
  11.     Raises:
  12.         无
  13.     """
  14.     example_size = len(features)
  15.     indices = list(range(example_size))
  16.     random.shuffle(indices)
  17.     for i in range(0, example_size, batch_size):
  18.         j = torch.LongTensor(indices[i:min(i + batch_size, example_size)])    # 防止溢出
  19.         yield features.index_select(0, j), labels.index_select(0, j)
  21. batch_size = 10
  22. for x, y in data_iter(batch_size, features, labels):
  23.     print(x, '\n', y)
  24.     break

运行结果

  1. tensor([[-0.0151, -0.3958],
  2.         [-0.0945, -0.7227],
  3.         [ 0.1960, -0.3565],
  4.         [ 0.3286,  0.1862],
  5.         [ 0.9063, -0.3101],
  6.         [-1.1899, -0.4032],
  7.         [-0.9397, -0.2831],
  8.         [-0.0709, -0.6024],
  9.         [-1.3366, -1.0776],
  10.         [ 2.3408,  0.6169]]) 
  11.  tensor([[5.5169],
  12.         [6.4762],
  13.         [5.7843],
  14.         [4.2247],
  15.         [7.0719],
  16.         [3.1794],
  17.         [3.2786],
  18.         [6.0992],
  19.         [5.1948],
  20.         [6.7959]])

3.2.3 初始化模型参数

参数随机初始化， 不要取同样的值，这在已经之前的笔记中讲过了。

  1. # 初始化模型参数
  2. w = torch.tensor(np.random.normal(0, 0.01, (feature_size, 1)), dtype=elem_type, requires_grad=True)
  3. b = torch.zeros(1, dtype=elem_type, requires_grad=True)
  4. print(w, '\n', b)

运行结果

  1. tensor([[0.0054],
  2.         [0.0009]], requires_grad=True) 
  3.  tensor([0.], requires_grad=True)

3.2.4 定义模型

  1. # 定义模型
  2. # 已在 d2lzh_pytorch 包中的 linreg 实现
  3. def linear_regression(x, w, b):
  4.     """
  5.     用矢量计算表达式描述线性回归的模型
  6.     Args:
  7.         x: 特征向量 x
  8.         w: 模型参数权重 w
  9.         b: 模型参数偏差 b
  10.     Returns:
  11.         预测的标签值
  12.     Raises:
  13.         无
  14.     """
  15.     return torch.mm(x, w) + b

3.2.5 定义损失函数

这次我们用的是 平方误差 函数。

  1. # 定义损失函数
  2. # 已在 d2lzh_pytorch 包中的 squared_loss 实现
  3. def lossfunc_square(y_predict, y):
  4.     """
  5.     计算当前参数下, 损失函数的数值
  6.     Args:
  7.         y_predict: 预测的标签值
  8.         y: 真是的标签值
  9.     Returns:
  10.         当前损失函数的值
  11.     Raises:
  12.         无
  13.     """
  14.     return (y_predict-y.view(y_predict.size())) ** 2 / 2

3.2.6 定义优化算法

我们采用小批量随机梯度下降， 关于击中常见的梯度下降算法， 可以查看此处

  1. # 定义优化算法
  2. # 已在 d2lzh_pytorch 包中的 sgd 实现
  3. def mbgd(params, lr, batch_size):
  4.     """
  5.     采用小批量样本 + 随机梯度下降算法来优化模型
  6.     Args:
  7.         params: 模型的参数
  8.         lr: 学习率
  9.         batch_size: 样本批次的规模
  10.     Returns:
  11.         无
  12.     Raises:
  13.         无
  14.     """
  15.     for param in params:
  16.         param.data -= lr * param.grad / batch_size

3.2.7 训练模型

在一个 迭代周期 中，我们将完整遍历一遍data_iter函数，即对训练数据集中 所有样本 都使用一次（假设样本数能够被批量大小整除）。
这里的迭代次数 iterate_num 和学习率lr都是 超参数 ，在实践中，大多超参数都需要通过反复试错来不断调节，也就是我们常常说的 调参工作 。虽然迭代周期数设得越大模型可能越有效，但是训练时间可能过长。而有关学习率对模型的影响，后续会再讲，之间的笔记中也有一定涉及。
选好我们的模型、损失函数(代价函数)，优化方法。当然现在我们也没得选，都是之前定义好的那些。框架的一大意义就在于它已经帮你将各种模型、损失函数、优化方法都已经帮你高效且正确地实现了，而你只需要根据实际问题需求选用。
每一次迭代后打印一下当前的损失值，查看一下训练效果，当然用 matplotlib可视化出来更好。

  1. # 训练模型
  2. # 学习率
  3. lr = 0.03
  4. # 迭代次数
  5. iterate_num = 5
  6. # 选择学习模型, 损失函数, 优化方法
  7. net = linear_regression
  8. lossfunc = lossfunc_square
  9. optimizer = mbgd
  11. # 开始迭代
  12. for i in range(iterate_num):
  13.     # 每一次迭代中都要使用训练集中全部样本一次
  14.     # x, y 分别是样本的特征和标签
  15.     for x, y in data_iter(batch_size, features, labels):
  16.         # 调用 sum(), 使结果用标量表示, 计算小批次样本的损失
  17.         current_lose = lossfunc(net(x, w, b), y).sum()
  18.         # 小批次样本的损失进行梯度反向传播
  19.         current_lose.backward()
  20.         # 优化模型参数
  21.         optimizer([w, b], lr, batch_size)
  22.         # 每次执行后梯度清零
  23.         w.grad.data.zero_()
  24.         b.grad.data.zero_()
  25.     # 计算整个训练集的损失, 查看学习效果
  26.     trainset_lose = lossfunc(net(features, w, b), labels).sum()
  27.     print("第{0}次训练和的损失={1:.4f}".format(i + 1, trainset_lose))

运行结果

  1. 第1次训练和的损失=35.7206
  2. 第2次训练和的损失=0.1288
  3. 第3次训练和的损失=0.0461
  4. 第4次训练和的损失=0.0461
  5. 第5次训练和的损失=0.0460

可以看出，训练得非常快，迭代 3 次后基本就稳定下来了。

最终结果

打印一下我们训练完的模型的参数。

  1. print("训练完成, 最终模型参数为")
  2. print("w =", w)
  3. print("b =", b)

运行结果

  1. w = tensor([[ 1.9997],
  2.         [-3.4002]], requires_grad=True)
  3. b = tensor([4.1998], requires_grad=True)

可以看到和我们生成数据时用的参数已经基本一致了。

小结

仅仅使用Tensor和autograd 这些基础模块，我们已经能比较方便地实现一个简单的线性回归了。接下来我们将利用 PyTorch 中更多更加方便的功能来进一步提高效率。

3.2 线性回归的从零开始实现.py