3.11.1 训练误差和泛化误差

从前面三个模型的训练结果可以发现，随着学习模型的迭代，当结果在训练集中的损失函数越来越趋向最小值，准确率越来越高，但是在测试集却不一定是绝对朝最优解发展的。这就涉及到训练误差(training error)和泛化误差(generalization error)的概念了。
训练误差：指模型在 训练数据集 上表现出的误差。
泛化误差：指模型在任意一个 测试数据样本 上表现出的误差的期望，并常常通过 测试数据集 上的误差来近似。
在机器学习里，通常假设训练集和测试集里的每一个样本都是 独立同分布的，基于该假设，给定任意一个机器学习模型，两种误差的期望是相同的。
在训练模型时，我们应该更多关注降低泛化误差。
**

3.11.2 模型的选择

模型选择(model selection)：评估候选模型并选出最佳模型的过程。
候选模型：可以是有着不同超参数的同类模型，比如隐藏层的层数、神经元数量、所用的激活函数。
验证数据集(validation data set)：独立于训练集和测试集，用于模型评估的一组数据，实际中由于数据不易获取，分隔界限可能会模糊。
K 折交叉验证(K-fold cross-validation)：将训练集分成 K 个划分，取一个做验证集，剩余 K-1 个做训练集，并进行轮换，最后对 K 次验证结果取平均。此法用于改善数据不够的情况。

3.11.3 欠拟合和过拟合

本节可参看吴恩达机器学习笔记
关于欠拟合和过拟合的现象在之前学习过，简单总结一下。
欠拟合（underfitting）：模型无法得到较低的训练误差。
过拟合（overfitting）：模型的训练误差远小于泛华误差。
常见影响因素包括模型复杂度，数据集规模。
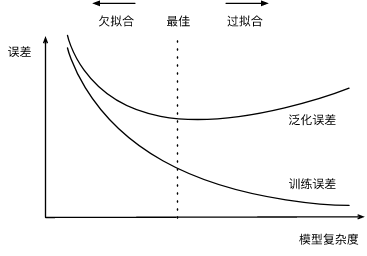
模型复杂度：以 K 阶多项式函数拟合3.11 模型选择、欠拟合和过拟合 - 图1为例，K 越大意味着模型参数越多，函数的选择空间越大，这样的模型有更高的复杂度。通过一张图看一下模型复杂度与两种现象的关系。更详细的信息传送门。
图片.png

3.11.4 多项式函数拟合实验

  • 生成数据集

我们的目标函数如下，当然在生成数据集时要加上噪点3.11 模型选择、欠拟合和过拟合 - 图3 。
3.11 模型选择、欠拟合和过拟合 - 图4

  1. # 生成数据集
  2. elem_type = torch.float
  3. train_size = test_size = 100
  4. true_w = torch.tensor([[1.2, -3.4, 5.6]]).t()
  5. true_b = 5
  6. feature_size = 3
  7. x = torch.randn((train_size + test_size, 1))
  8. features = torch.cat((x, torch.pow(x, 2), torch.pow(x, 3)), 1)
  9. labels = torch.mm(features, true_w) + true_b
  10. labels += torch.normal(0, 0.01, size=labels.size(), dtype=elem_type)
  11. print(x[:2], '\n', features[:2], '\n', labels[:2])

看一下前两组样本。

  1. tensor([[ 1.4096],
  2.         [-0.0016]]) 
  3.  tensor([[ 1.4096e+00,  1.9871e+00,  2.8011e+00],
  4.         [-1.5639e-03,  2.4457e-06, -3.8249e-09]]) 
  5.  tensor([[10.6364],
  6.         [-0.0203]])
  • 绘图函数

用红蓝两色分别画出两组数据的曲线并显示图例。

  1. def semilogy(x_label, y_label, x1_vals, y1_vals, x2_vals, y2_vals, legend):
  2.     """
  3.     绘制两条曲线和图例.
  4.     Args:
  5.         x_label: x 轴标签
  6.         y_label: y 轴标签
  7.         x1_vals: 第 1 组 x 轴数据
  8.         y1_vals: 第 1 组 y 轴数据
  9.         x2_vals: 第 2 组 x 轴数据
  10.         y2_vals: 第 2 组 y 轴数据
  11.         legend: 图例名称
  12.     Returns:
  13.         无
  14.     Raises:
  15.         无
  16.     """
  17.     plt.xlabel(x_label)
  18.     plt.ylabel(y_label)
  19.     # y 轴取 log
  20.     plt.semilogy(x1_vals, y1_vals, "r")
  21.     plt.semilogy(x2_vals, y2_vals, "b")
  22.     # 绘制图例
  23.     plt.legend(legend)
  24.     plt.show()
  • 训练模型
  1. def fit_and_plot(train_features, train_labels, test_features, test_labels):
  2.     """
  3.     训练模型并可视化训练结果和测试结果.
  4.     Args:
  5.         train_features: 训练集的特征
  6.         train_labels: 训练集的标签
  7.         test_features: 测试集的特征
  8.         test_labels: 测试集的标签
  9.     Returns:
  10.         无
  11.     Raises:
  12.         无
  13.     """
  14.     # 训练准备
  15.     iterate_num = 100
  16.     loss_func = torch.nn.MSELoss()
  17.      net = torch.nn.Linear(train_features.shape[-1], 1)
  18.     optimizer = torch.optim.SGD(net.parameters(), lr=0.01)
  19.     batch_size = min(10, train_labels.shape[0])
  20.     train_set = torch_data.TensorDataset(train_features, train_labels)
  21.     train_set_iter = torch_data.DataLoader(train_set, batch_size, shuffle=True)
  22.     # 存放学习后的误差数据点
  23.     train_lose_array, test_lose_array = [], []
  25.     for i in range(iterate_num):
  26.         for x, y in train_set_iter:
  27.             y_output = net(x)
  28.             current_lose = loss_func(y_output, y.view(y_output.size()))
  29.             optimizer.zero_grad()
  30.             current_lose.backward()
  31.             optimizer.step()
  32.         train_lose_array.append(loss_func(net(train_features), train_labels).item())
  33.         test_lose_array.append(loss_func(net(test_features), test_labels).item())
  34.         print("第{0}个训练周期后: 训练误差={1:.4f}, 泛化误差={2:.4f}".format(
  35.               i + 1, train_lose_array[-1], test_lose_array[-1]))
  36.     print("训练后结果:weight={0}, bias={1}".format(
  37.           net.weight.data, net.bias.data))
  38.     semilogy("epochs", "lose",
  39.              range(1, iterate_num + 1), train_lose_array,
  40.              range(1, iterate_num + 1), test_lose_array,
  41.              ["train", "test"])
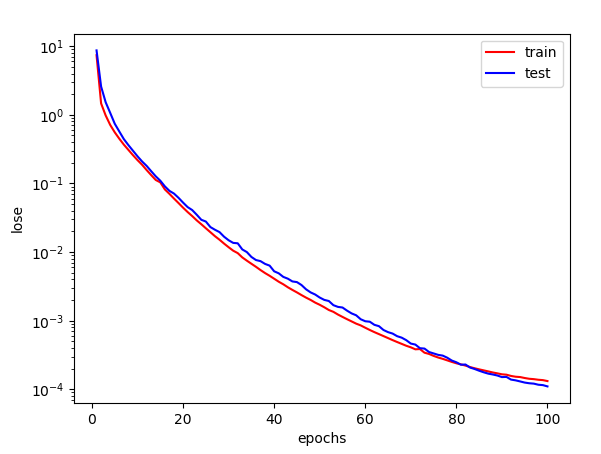
  1. 正常拟合
    1. # 正常拟合
    2. fit_and_plot(features[:train_size, :], labels[:train_size],
    3.           features[train_size:, :], labels[train_size:])

两者基本上相差不大。

  1. 第100个训练周期后: 训练误差=0.0001, 泛化误差=0.0002
  2. 训练后结果:
  3. weight=tensor([[ 1.1941, -3.3993,  5.6009]]),
  4.  bias=tensor([4.9984])

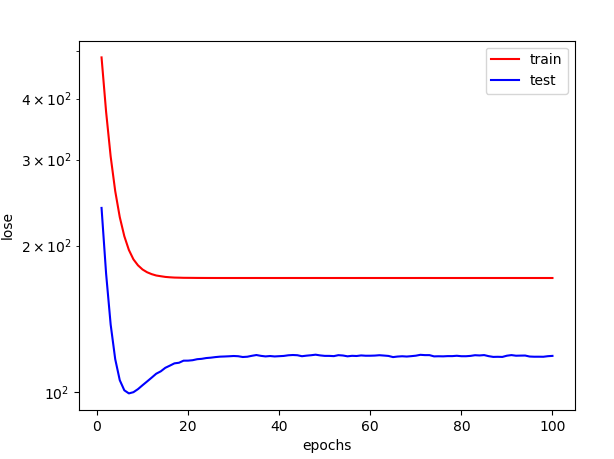
图片.png

  1. 欠拟合

这次我们做点手脚，只用一阶 x 这一个特征。

  1. # 欠拟合
  2. fit_and_plot(x[:train_size, :], labels[:train_size],
  3.              x[train_size:, :], labels[train_size:])

显然，这样一来模型就过于简单了，训练一段时间后，误差就基本不再下降。
可能由于模型实在太简单了，我遇到了训练误差比泛化误差小的情况。

  1. 第96个训练周期后: 训练误差=171.6151, 泛化误差=118.3576
  2. 第97个训练周期后: 训练误差=171.6150, 泛化误差=118.3711
  3. 第98个训练周期后: 训练误差=171.6153, 泛化误差=118.3389
  4. 第99个训练周期后: 训练误差=171.6140, 泛化误差=118.6643
  5. 第100个训练周期后: 训练误差=171.6144, 泛化误差=118.8265
  6. 训练后结果:
  7. weight=tensor([[20.9044]]),
  8.  bias=tensor([0.3815])

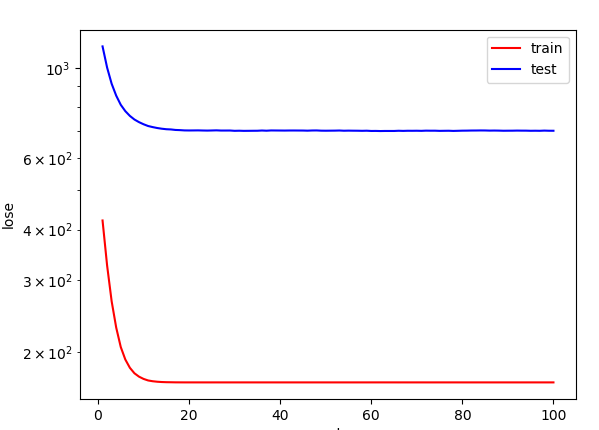
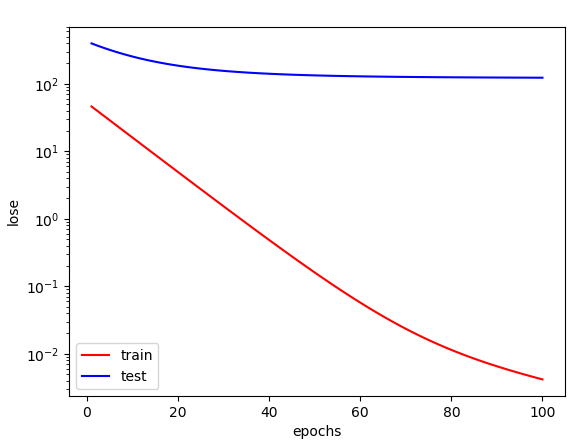
图片.png图片.png

  1. 过拟合

这一次我们减少训练数据，只给 2 个。

  1. # 过拟合
  2. fit_and_plot(features[0:2, :], labels[0:2],
  3.              features[train_size:, :], labels[train_size:])

尽管学习后的模型对这两个样本的拟合非常优秀，但是泛化能力也大大降低。

  1. 第100个训练周期后: 训练误差=0.0042, 泛化误差=122.9024
  2. 训练后结果:
  3. weight=tensor([[1.4418, 2.1822, 2.5563]]),
  4.  bias=tensor([1.9778])

图片.png
3.11.4 多项式函数拟合实验.py