2.3.2 Tensor

requires_grad=True 的 Tensor 其上的所有操作将被 追踪 ，完成计算后，可以调用 backward() 完成所有梯度计算。
每个Tensor都有一个.grad_fn属性，该属性表示该 Tensor 是不是通过某些运算得到的，若是，则grad_fn返回一个 与这些运算相关的对象 ，否则是 None 。

# 创建一个 Tensor 并设置 requires_grad=True 表示需要求导
a = torch.ones((2, 2), requires_grad=True)
print(a)
print(a.grad_fn)
b = a + 2
print(b)
print(b.grad_fn)

运行结果

tensor([[1., 1.],
        [1., 1.]], requires_grad=True)
None
tensor([[3., 3.],
        [3., 3.]], grad_fn=<AddBackward0>)
<AddBackward0 object at 0x7f8e1cdb4d90>

a 是直接创建的，所以它没有grad_fn, 而 b 是通过一个加法操作创建的，所以它有一个为<AddBackward0>的grad_fn。
a 这类不依赖其他 Tensor 的 Tensor ， 又被称为叶子节点。

# 叶子节点
print(a.is_leaf)    # True
print(b.is_leaf)    # False

再来看一些稍微复杂的运算， 可以看出grad_fn 属性描述了梯度函数，即 Tensor 是通过何种运算创建而来。

c = b * b * 3
d = c.mean()
print(c)
print(d)

运行结果

tensor([[27., 27.],
        [27., 27.]], grad_fn=<MulBackward0>)
tensor(27., grad_fn=<MeanBackward0>)

通过 requires_grad_() 来设置 require_grad 属性

# 改变 require_grad 属性
# 缺省时 require_grad = False
a = torch.randn((2, 2))
a = (a * 3)/(a - 1)
print(a.requires_grad)  # False
a.requires_grad_(True)
print(a.requires_grad)  # True

2.3.2 Tensor.py

2.3.3 梯度

1. 理解 backward() 和 **tensor.grad**

**

• Tensor 执行自身的 backward() 函数，此时之前参与运算并生成当前 Tensor 的 叶子节点 将会保存其梯度在 叶子节点 的 grad 属性中。 backward() 函数接受参数，表示 在特定位置求梯度值 ，该参数应和调用 backward() 函数的 Tensor 的 维度相同 ，或者是可 broadcast 的维度。默认为 torch.tensor(1.) ，也就是在当前梯度为标量 1 的位置求 叶子节点的梯度 。
• 默认同一个运算得到的 Tensor 仅能进行一次 backward() 。再次运算得到的 Tesnor ，可以再次进行 backward() 。
• 当多个 Tensor 从相同的源 Tensor 运算得到，这些运算得到的 Tensor 的 backwards() 方法将向源 Tensor 的 grad 属性中进行数值累加。
• 我们不允许张量对张量求导，只允许标量对张量求导，求导结果是和自变量同形的张量。
• 假设 x 经过一番计算得到 y ，那么 y.backward(w) 求的不是 y 对 x 的导数，而是 torch.sum(y*w) 对 x 的导数， w 可以视为 y 的各分量的权重。这里的乘法 * 是 矩阵点乘
• x 和 x.grad 是同形 Tensor

参考链接1 参考链接2

out 是一个标量， 所以调用 backward() 时不需要指定求导变量

# 计算梯度
x = torch.ones(2, 2, requires_grad=True)
y = x + 2
z = y * y * 3
# 标量 out
out = z.mean()
print(out)
# 相当于 out.backward(torch.tensor(1.))
out.backward()
# out 关于 x 的梯度
print(x.is_leaf, y.is_leaf, z.is_leaf, out.is_leaf)
print(x.grad)
print(y.grad)
print(z.grad)
print(out.grad)

在 x.grad 中我们可以看到 out 关于 x 的梯度， 即，

运行结果

tensor(27., grad_fn=<MeanBackward0>)
True False False False
tensor([[4.5000, 4.5000],
        [4.5000, 4.5000]])
None
None
None

关于数学的补充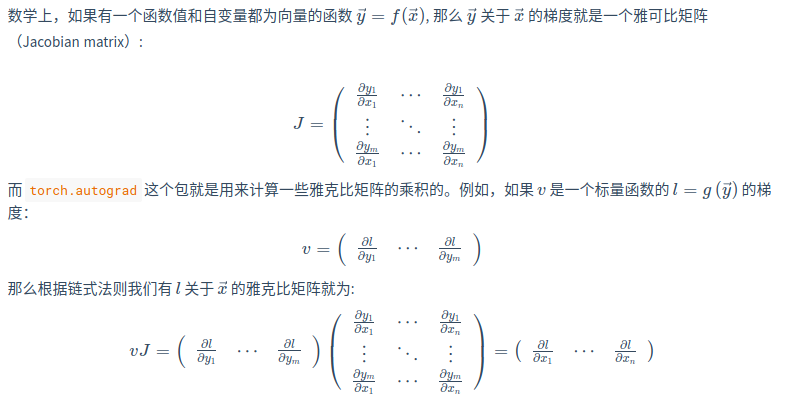

grad 在反向传播过程中是 累加的(accumulated) ，这意味着每一次运行反向传播，梯度都会累加之前的梯度，所以一般在反向传播之前需把梯度清零。

# 再来一次反向传播
out2 = x.sum()
out2.backward() # 梯度为 1
print(x.grad)
out3 = x.sum()
x.grad.zero_()
x.grad.detach().zero_()
out3.backward()
print(x.grad)

运行结果

tensor([[5.5000, 5.5000],
        [5.5000, 5.5000]])
tensor([[1., 1.],
        [1., 1.]])

现在我们通过一个例子深入理解一下 backward() 在计算什么

# 理解 backward() 的计算
x = torch.tensor([1., 2., 3., 4.], requires_grad=True)
y = 2 * x
z = y.view(2, 2)
print(z)
# z 不是标量， 传入一个同形 Tensor
v = torch.tensor([[1., 0.1],
                  [0.01, 0.001]], dtype=torch.float)
z.backward(v)
print(x.grad)

运行结果

tensor([[2., 4.],
        [6., 8.]], grad_fn=<ViewBackward>)
tensor([2.0000, 0.2000, 0.0200, 0.0020])

还原一下计算的过程

x.grad 中的
所以最终

1. 中断梯度追踪 ```python

   中断梯度追踪

   x = torch.tensor(1.0, requires_grad=True) y1 = x ** 2

   被包围的代码块将停止追踪

   with torch.no_grad(): y2 = x ** 3

y3 = y1 + y2 y3.backward() print(x, x.requires_grad, x.is_leaf) print(y1, y1.requires_grad, y1.is_leaf) print(y2, y2.requires_grad, y2.is_leaf) print(y3, y3.requires_grad, y3.is_leaf) print(x.grad) print(y2.grad)

RuntimeError: element 0 of tensors does not require grad and does not have a grad_fn

y2.backward()

运行结果
```python
tensor(1., requires_grad=True) True True
tensor(1., grad_fn=<PowBackward0>) True False
tensor(1.) False True
tensor(2., grad_fn=<AddBackward0>) True False
tensor(2.)
None

都是通过 x 经过各种运算的到的 y1 y2 y3 ，但只有 y2 是不需要追踪的， 且 y2 也被视为 叶子节点。
此时 y3 执行反向传播，计算梯度时与 y2 相关的部分会被完全忽略。
像 y2 这样 require_grad=True 的 Tensor 是不能执行 backward() 方法的，否则会报错。

1. 对 tensor.data 进行操作

如果我们想要修改tensor的数值，但是又不希望被autograd记录（即不会影响反向传播），那么我们可以对tensor.data进行操作。

教程那个的例子我并没有看懂， 这样求梯度本来就是一个常数 2，我觉得也谈不上什么影响不影响，后续再说 mark一下

# 对 data 进行操作
x = torch.ones(1, requires_grad=True)
# x.data 是一个独立于计算图之外的 Tensor
print(x.data, x.data.requires_grad)
y = x ** 2
x.data *= 100
y.backward()
# 更改数值影响原 tensor 
print(x)
print(x.grad)
# x.data.grad 不受影响
print(x.data.grad)

运行结果

tensor([1.]) False
tensor([100.], requires_grad=True)
tensor([200.])
None

2.3.3 梯度.py