1 损失函数简介
** 损失函数**是用来估量模型的**预测值f(x)**与**真实值Y**的不一致程度,它是一个**非负实值函数**,通常使用**L(Y, f(x))**来表示,损失函数越小,模型的鲁棒性就越好。损失函数是**经验风险函数**的核心部分,也是**结构风险函**数重要组成部分。**损失函数**分为**经验风险损失函数**和**结构风险损失函数**。**经验风险损失函数**指预测结果和实际结果的差别,**结构风险损失函数**是指经验风险损失函数加上正则项。通常可以表示成如下式子:<br /> 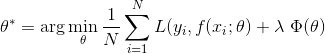<br /> 其中,前面的**均值函数**表示的是**经验风险函数**,L代表的是**损失函数**,后面的Φ是**正则化项**或者叫**惩罚项**,它可以是**L1**,也可以是**L2**,或者其他的**正则函数**。整个式子表示的意思是找到**使目标函数最小时的θ值**。下面主要列出几种常见的损失函数:
- log对数损失函数(逻辑回归)
- 平方损失函数(最小二乘法)
- 指数损失函数(Adaboost)
- Hinge损失函数(SVM)
- 0-1损失
绝对值损失
2 log对数损失函数(逻辑回归)
**Logistic回归**的**损失函数**就是**对数损失函数**,在Logistic回归的推导中,它假设样本服从**伯努利分布(伯努利分布**亦称“零一分布”、“两点分布”。称随机变量X有伯努利分布, 参数为p(0<p<1),如果它分别以概率**p**和**1-p**取1和0为值。EX= p,DX=p(1-p)**)**分布,然后求得满足**该分布的似然函数**,接着**用对数求极值**。**Logistic回归**并没有求对数似然函数的最大值,而是把极大化当做一个思想,进而推导它的风险函数为最小化的负的似然函数。从损失函数的角度上,它就成为了log损失函数,其标准形式: <br /> 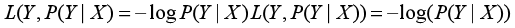<br />Logistic回归目标式子如下:<br /> 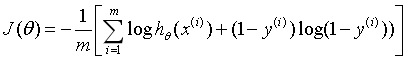<br />逻辑回归模型详见:[https://blog.csdn.net/weixin_39910711/article/details/81607386]()
3 平方损失函数(最小二乘法, Ordinary Least Squares )
**最小二乘法**是**线性回归**的一种方法,它将回归的问题转化为了**凸优化的问题**。最小二乘法的基本原则是:**最优拟合曲线**应该使得所有点到回归直线的距离和最小。通常用**欧式距离**进行距离的度量。当样本个数为n时,此时的损失函数变为:<br /> 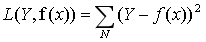<br /> ** Y-f(X)**表示的是**残差**,整个式子表示的是残差的平方和,而我们的目的就是**最小化这个目标函数值**(注:该式子未加入正则项),也就是最小化残差的平方和。<br /> 而在实际应用中,通常会使用**均方差(MSE)**作为一项衡量指标,公式如下:<br /> 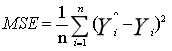
4 指数损失函数(Adaboost)
学过Adaboost算法的人都知道,它是前向分步加法算法的特例,是一个加和模型,损失函数就是指数函数。在Adaboost中,经过m此迭代之后,可以得到:<br /> <br /> Adaboost每次迭代时的目的是为了找到最小化下列式子时的**参数 α**和**G**:<br /> <br /> ** 指数损失函数(exp-loss)**的标准形式如下:<br /> 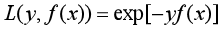<br /> 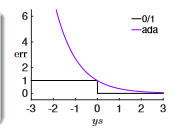<br /> 可以看出,Adaboost的目标式子就是指数损失,在给定**n个样本**的情况下,Adaboost的损失函数为:<br /> 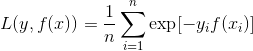
5 Hinge损失函数(SVM)
在机器学习算法中,**hinge损失函数**和**SVM**是息息相关的。在**线性支持向量机**中,最优化问题可以等价于下列式子:<br /> <br /> 下面来对式子做个变形,令:<br /> 于是,原式就变成了:<br /> 式子就可以表示成: <br /> 可以看出,该式子与下式非常相似:<br /> <br /> 其中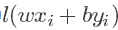就是**hinge损失函数**,后面相当于**L2正则项**。 <br /> Hinge loss用于**最大间隔(maximum-margin)分类**,其中最有代表性的就是支持向量机SVM。<br />** Hinge函数的标准形式:**<br /> 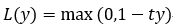<br /> 其中,**t为目标值(-1或+1)**,y是**分类器**输出的预测值,并不直接是**类标签**。其含义为,当t和y的符号相同时(表示y预测正确)并且|y|≥1时,hinge loss为0;当t和y的符号相反时,hinge loss随着y的增大线性增大。<br />SVM详见:[https://blog.csdn.net/weixin_39910711/article/details/82356973]()
6 0-1损失函数
在分类问题中,可以使用**函数的正负号**来进行**模式判断**,函数值本身的大小并不是很重要,**0-1损失函数**比较的是**预测值**与**真实值**的符号是否相同,**0-1损失**的具体形式如下:<br /> 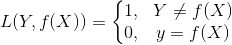
7 绝对值损失函数
绝对损失函数的意义和平方损失函数差不多,只不过是取了**绝对值**而不是求平方,差距不会被平方放大,其形式为:<br /> 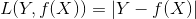<br />

