机器学习需要的数学基础

机器学习是近几年炙手可热的话题。每天都有新的应用和模型进入人们的视野。世界各地的研究人员每天所公布的实验结果都显示了机器学习领域所取得的巨大进步。
技术工作者参加各类课程、搜集各种资料，希望使用这些新技术改进他们的应用。但在很多情形下，要理
解机器学习需要深厚的数学功底。这就为那些虽然具有良好的算法技能，但数学概念欠佳的程序员们设置了较高的门槛。
为了掌握它们背后的动机和理论，有必要回顾并建立所有基本推理知识体系，包括统计、概率和微积分。
下面先从一些基本的统计概念开始。

1.3.1　统计学——不确定性建模的基本支柱

统计学可以定义为使用数据样本，提取和支持关于更大样本数据结论的学科。考虑到机器学习是研究数据属性和数据赋值的重要组成部分，本书将使用许多统计概念来定义和证明不同的方法。

描述性统计学——主要操作

接下来将从定义统计学的基本操作和措施入手，并将基本概念作为起点。

（1）平均值（Mean）
这是统计学中直观、常用的概念。给定一组数字，该集合的平均值是所有元素之和除以集合中元素的数量。
平均值的公式如下。

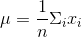
虽然这是一个非常简单的概念，但本书还是提供了一个Python代码示例。在这个示例中，我们将创建样本集，并用线图表示它，将整个集合的平均值标记为线，这条线应该位于样本的加权中心。它既可以作为Python语法的介绍，也可以当作Jupyter Notebook的实验。代码如下。

import matplotlib.pyplot as plt #Import the plot library
def mean(sampleset):  #Definition header for the mean function
    total=0
    for element in sampleset:
        total=total+element
    return total/len(sampleset)
myset=[2.,10.,3.,6.,4.,6.,10.] #We create the data set
mymean=mean(myset) #Call the mean funcion
plt.plot(myset)  #Plot the dataset
plt.plot([mymean] * 7)  #Plot a line of 7 points located on the mean

该程序将输出数据集元素的时间序列，然后在平均高度上绘制一条线。
如图1.6所示，平均值是描述样本集趋势的一种简洁（单值）的方式。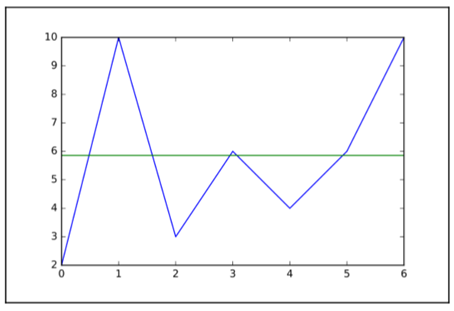

图1.6　用平均值描述样本集趋势
因为在第一个例子中，我们使用了一个非常均匀的样本集，所以均值能够有效地反映这些样本值。
下面再尝试用一个非常分散的样本集（鼓励读者使用这些值）来进行实验，如图1.7所示。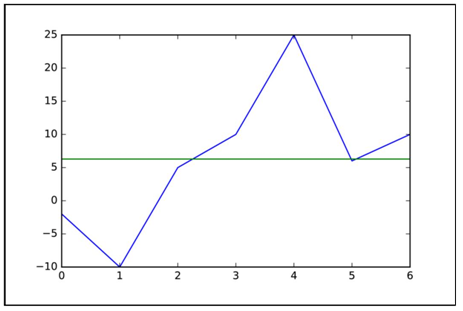

图1.7　分散样本集的趋势

（2）方差（Variance）
正如前面的例子所示，平均值不足以描述非均匀或非常分散的样本数据。
为了使用一个唯一的值来描述样本值的分散程度，需要介绍方差的概念。它需要将样本集的平均值作为起点，然后对样本值到平均值的距离取平均值。方差越大，样本集越分散。
方差的规范定义如下。

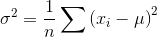
下面采用以前使用的库，编写示例代码来说明这个概念。为了清楚起见，这里重复mean函数的声明。代码如下。

import math #This library is needed for the power operation
def mean(sampleset):  #Definition header for the mean function
    total=0
    for element in sampleset:
        total=total+element
    return total/len(sampleset)
def variance(sampleset):  #Definition header for the mean function
    total=0
    setmean=mean(sampleset)
    for element in sampleset:
        total=total+(math.pow(element-setmean,2))
    return total/len(sampleset)
myset1=[2.,10.,3.,6.,4.,6.,10.]  #We create the data set
myset2=[1.,-100.,15.,-100.,21.]
print "Variance of first set:" + str(variance(myset1))
print "Variance of second set:" + str(variance(myset2))

前面的代码将输出以下结果。

Variance of first set:8.69387755102
Variance of second set:3070.64

正如上面的结果所示，当样本值非常分散时，第二组的方差要高得多。因为计算距离平方的均值是一个二次运算，它有助于表示出它们之间的差异。

（3）标准差（Standard Deviation）
标准差只是对方差中使用的均方值的平方性质进行正则化的一种手段。它有效地将该项线性化。这个方法可以用于其他更复杂的操作。
以下是标准差的表示形式。

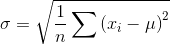
1.3.2　概率与随机变量

概率与随机变量对于理解本书所涉概念极为重要。

概率（Probability）是一门数学学科，它的主要目标就是研究随机事件。从实际的角度讲，概率试图从可能发生的所有事件中量化事件发生的确定性（或者不确定性）。

1．事件

为了理解概率，我们首先对事件进行定义。在给定的实验中，执行确定的动作可能出现不同的结果。事件就是该实验中所有可能结果的子集。
关于事件的一个例子就是摇骰子时出现的特定数字，或者装配线上出现的某种产品缺陷。

（1）概率
按照前面的定义，概率是事件发生的可能性。概率被量化为0～1之间的实数。当事件发生的可能性增加时，概率P也按照接近于1的趋势增加。事件发生概率的数学表达式是P(E)。

（2）随机变量和分布
在分配事件概率时，可以尝试覆盖整个样本，并为样本空间中的每个可能分配一个概率值。
这个过程具有函数的所有特征。对于每一个随机变量，都会为其可能的事件结果进行赋值。这个函数称为随机函数。
这些变量有以下两种类型。

• 离散（Discrete）：结果的数量是有限的或可数无穷的。
• 连续（Continuous）：结果集属于连续区间。

这个概率函数也称为概率分布（Probability Distribution）。

2．常用概率分布

在多种可能的概率分布中，有些函数由于其特殊的性质或它们所代表问题的普遍性而被研究和分析。
本书将描述那些常见的概率分布。它们对机器学习的发展具有特殊的影响。

（1）伯努利分布（Bernoulli Distribution）
从一个简单的分布开始：像抛硬币一样，它具有二分类结果（binary outcome）。
这个分布表示单个事件。该事件中1（正面）的概率为p，0（反面）的概率为1−p。
为了实现可视化，可以使用np（NumPy库）生成大量伯努利分布的事件，并绘制该分布的趋势。它有以下两种可能的结果。代码如下。

plt.figure()
distro = np.random.binomial(1, .6, 10000)/0.5
plt.hist(distro, 2 , normed=1)

下面通过图1.8中的直方图显示二项分布（Binomial Distribution），可以看出结果概率的互补性质。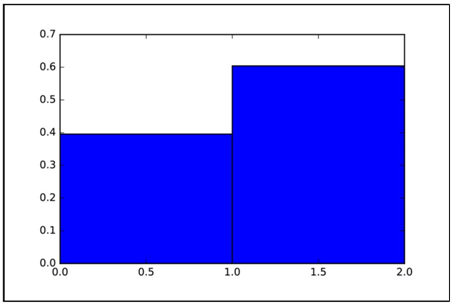

图1.8　二项分布

可能结果的概率互补趋势非常明显。现在用更多的可能结果来补充模型。当结果的数目大于2时，采用多项式分布（Multinomial Distribution）。代码如下。

plt.figure()
distro = np.random.binomial(100, .6, 10000)/0.01
plt.hist(distro, 100 , normed=1)
plt.show()

结果如图1.9所示。

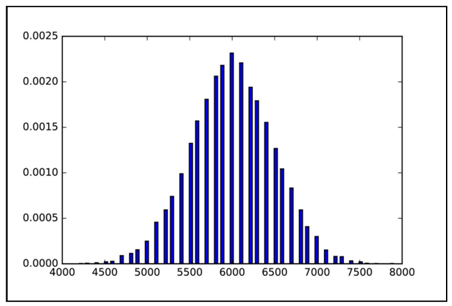
图1.9　100种可能结果的多项式分布

（2）均匀分布（Uniform Distribution）
这种非常常见的分布是本书出现的第一个连续分布。顾名思义，对于域的任何区间，它都有一个恒定的概率值。
a和b是函数的极值，为了使函数积分为1，这个概率值为1/(b−a)。
下面用一个非常规则的直方图生成样本均匀分布的图。代码如下。

plt.figure()
uniform_low=0.25
uniform_high=0.8
plt.hist(uniform, 50, normed=1)
plt.show()

结果如图1.10所示。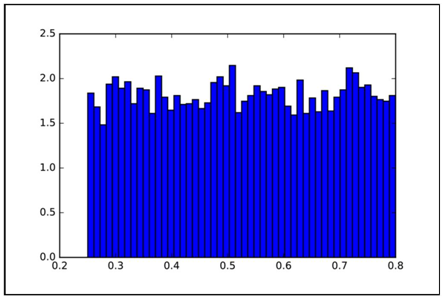

图1.10　均匀分布
（3）正态分布（Normal Distribution）
这是一种常见的连续随机函数，也称作高斯函数（Gaussian Function）。虽然表达式有些复杂，但它只需要用均值和方差来定义。
这是函数的标准形式。

查看下面的代码。

import matplotlib.pyplot as plt #Import the plot library
import numpy as np
mu=0.
sigma=2.
distro = np.random.normal(mu, sigma, 10000)
plt.hist(distro, 100, normed=True)
plt.show()

图1.11所示为生成的分布直方图。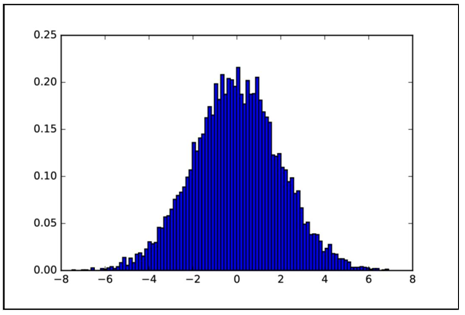

图1.11　正态分布

（4）Logistic分布（Logistic Distribution）

它类似于正态分布，但在形态上与正态分布存在较大差异，其具有细长的尾部。它的重要性在于积累分布函数（Cumulative Distribution Function，CDF），下面的章节中将会使用到它，读者会觉得它看起来很熟悉。
下面这段代码表示了它的基本分布。

import matplotlib.pyplot as plt #Import the plot library
import numpy as np
mu=0.5
sigma=0.5
distro2 = np.random.logistic(mu, sigma, 10000)
plt.hist(distro2, 50, normed=True)
distro = np.random.normal(mu, sigma, 10000)
plt.hist(distro, 50, normed=True)
plt.show()

结果如图1.12所示。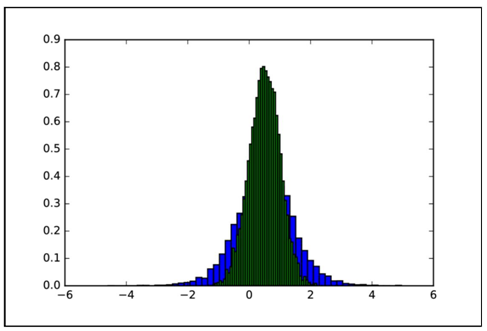

图1.12　Logistic分布（绿）和正态分布（蓝）[1]

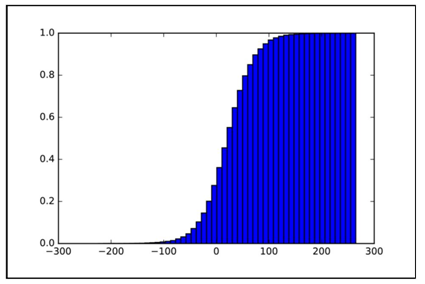
如前所述，计算Logistic分布的积累分布函数时，读者将看到一个非常熟悉的图形，即Sigmoid曲线。后面在回顾神经网络激活函数时，还将再次看到它。代码如下。

plt.figure()
logistic_cumulative = np.random.logistic(mu, sigma, 10000)/0.02
plt.hist(logistic_cumulative, 50, normed=1, cumulative=True)
plt.show()

结果如图1.13所示。

图1.13　逆Logistic分布

1.3.3　概率函数的统计度量

这一节中，将看到概率中常见的统计度量。首先是均值和方差，其定义与前面在统计学中看到的定义没有区别。

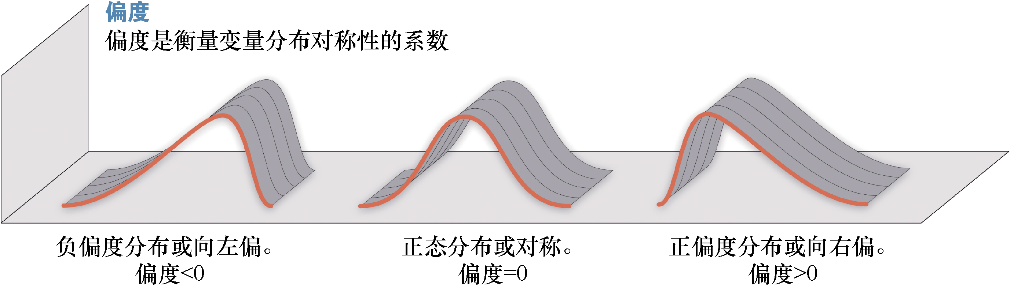
1．偏度（Skewness）

它表示了一个概率分布的横向偏差，即偏离中心的程度或对称性（非对称性）。一般来说，如果偏度为负，则表示向右偏离；如果为正，则表示向左偏离。

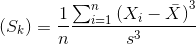
图1.14描绘了偏度的统计分布。

图1.14　分布形状对偏度的影响

2．峰度（Kurtosis）

峰度显示了分布的中心聚集程度。它定义了中心区域的锐度，也可以反过来理解，就是函数尾部的分布方式。
峰度的表达式如下。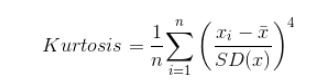

由图1.15可以直观地理解这些新的度量。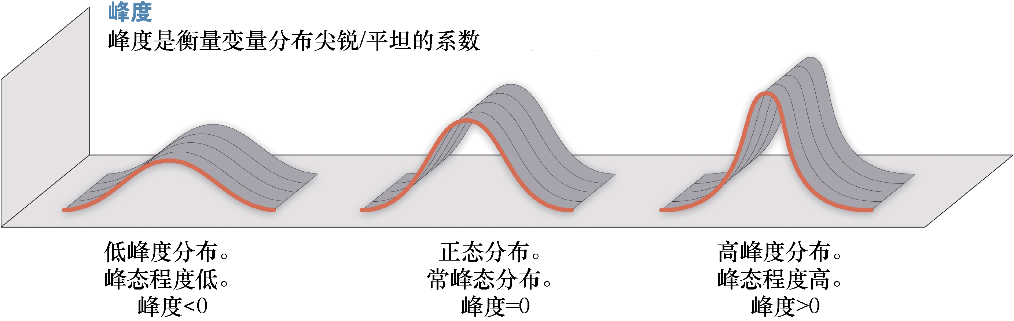

图1.15　分布形状对峰度的影响

1.3.4　微分基础

为了覆盖机器学习的基础知识，尤其是像梯度下降（Gradient Descent）这样的学习算法，本书将介绍微分学所涉及的概念。

1.3.5　预备知识

介绍覆盖梯度下降理论所必需的微积分术语需要很多章节，因此我们假设读者已经理解连续函数的概念，如线性、二次、对数和指数，以及极限的概念。
为了清楚起见，我们将从一元函数的概念开始，然后简单地涉及多元函数。

1．变化分析——导数

在前一节中介绍了函数的概念。除了在整个域中定义的常值函数之外，所有函数的值都是动态的。这意味着在x确定的情况下，f(x1)与f(x2)的值是不同的。
微分学的目的是衡量变化。对于这个特定的任务，17世纪的许多数学家（莱布尼兹和牛顿是杰出的倡导者）努力寻找一个简单的模型来衡量和预测符号定义的函数如何随时间变化。
这项研究将引出一个奇妙的概念—— 一个具有象征性的结果，在一定条件下，表示在某个点上函数变化的程度，以及变化的方向。这就是导数的概念。

在斜线上滑动

如果想测量函数随时间的变化，首先要取一个函数值，在其后的点上测量函数。第一个值减去第二个值，就得到函数随时间变化的程度。代码如下。

import matplotlib.pyplot as plt
import numpy as np
 %matplotlib inline
def quadratic(var):
    return 2* pow(var,2)
x=np.arange(0,.5,.1)
plt.plot(x,quadratic(x))
plt.plot([1,4], [quadratic(1), quadratic(4)], linewidth=2.0)
plt.plot([1,4], [quadratic(1), quadratic(1)], linewidth=3.0,
label="Change in x")
plt.plot([4,4], [quadratic(1), quadratic(4)], linewidth=3.0,
label="Change in y")
plt.legend()
plt.plot (x, 10*x -8 )
plt.plot()

前面的代码示例首先定义了一个二次方程（2×x2），然后定义arange函数的域（0～0.5，步长0.1）。
定义一个区间，测量y随x的变化，并画出测量的直线，如图1.16所示。

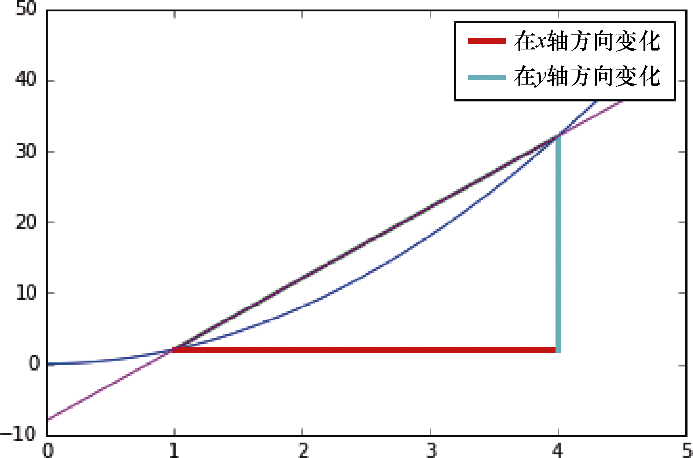
图1.16　求导操作起始设置的初始描述

在x=1和x=4处测量函数，并定义这个区间的变化率。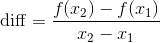

根据公式，示例程序的运行结果是(36−0)/3=12。
这个方法可以用来近似测量，但它太依赖于测量的点，并且必须在每个时间间隔都进行测量。
为了更好地理解函数的动态变化，需要能够定义和测量函数域中每个点的瞬时变化率。因为是测量瞬时变化，所以需要减少域x值之间的距离，使各点之间的距离尽量缩短。我们使用初始值x和后续值x + Δx来表示这个方法。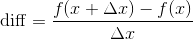

下面的代码中，通过逐步减小Δx来逼近差分值。代码如下。

initial_delta = .1
x1 = 1
for power in range (1,6):
    delta = pow (initial_delta, power)
    derivative_aprox= (quadratic(x1+delta) - quadratic (x1) )/
    ((x1+delta) - x1 )
    print "del    ta: " + str(delta) + ", estimated derivative: " +
    str(derivative_aprox)

在上面的代码中，首先定义了初始增量Δ，从而获得初始近似值。然后在差分函数中，对0.1进行乘方运算，幂逐步增大，Δ的值逐步减小，得到如下结果。

delta: 0.1, estimated derivative: 4.2
delta: 0.01, estimated derivative: 4.02
delta: 0.001, estimated derivative: 4.002
delta: 0.0001, estimated derivative: 4.0002
delta: 1e-05, estimated derivative: 4.00002

随着Δ值的逐步减小，变化率将稳定在4左右。但这个过程什么时候停止呢？事实上，这个过程可以是无限的，至少在数值意义上是这样。

这就引出了极限的概念。在定义极限的过程中，使 Δ 无限小，得到的结果称之为f(x)的导数或f ‘ (x)，公式如下。

但是数学家们并没有停止烦琐的计算。他们进行了大量的数值运算（大多是在17世纪手工完成的），并希望进一步简化这些操作。

现在构造一个函数，它可以通过替换x的值来得到相应的导数。对于不同的函数族，从抛物线(y=x2+b)开始，出现了更复杂的函数（见图1.17），这一巨大的进步发生在17世纪。

图1.17　复杂函数

2．链式法则

在函数导数符号确定后，一个非常重要的结果就是链式法则。莱布尼茨在1676年的一篇论文中首次提到这个公式。它可以通过非常简单优雅的方式求解复合函数的导数，从而简化复杂函数的求解。
为了定义链式法则，假设有一个函数f，F=f (g(x))，那么导数可以定义如下。

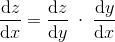
链式法则允许对输入值为另一个函数的方程求导。这与搜索函数之间关联的变化率是一样的。链式法则是神经网络训练阶段的主要理论概念之一。因为在这些分层结构中，第一层神经元的输出将是下一层的输入。在大多数情况下，复合函数包含了一层以上的嵌套。

偏导数（Partial Derivative）

到目前为止，本书一直使用单变量函数。但是从现在开始，将主要介绍多变量函数。因为数据集将不止包含一个列，并且它们中的每一列将代表不同的变量。

在许多情况下，需要知道函数在一个维度中的变化情况，这将涉及数据集的一列如何对函数的变化产生影响。
偏导数的计算包括将已知的推导规则应用到多变量函数，并把未被求导的变量作为常数导出。
看一看下面的幂函数求导法则。

f(x, y) = 2x3y

当这个函数对x求导时，y作为常量。可以将它重写为3 ∙ 2 y x2，并将导数应用到变量x，得到以下结果。

d/dx(f(x, y)) = 6y * x2

使用这些方法，可以处理更复杂的多变量函数。这些函数将是特征集的一部分，通常由两个以上的变量组成。