一、数据质量分析
数据质量分析的主要任务是检查原始数据中是否存在脏数据,脏数据一般是指不符合要 求,以及不能直接进行相应分析的数据。在常见的数据挖掘工作中,脏数据包括如下内容。
1)缺失值。
2)异常值。
3)不一致的值。
4)重复数据及含有特殊符号(如#、¥、*)的数据。
1.1 缺失值分析
(1)缺失值产生的原因
(2)缺失值的影响
(3)缺失值的分析
从总体上来说,缺失值的处理分为删除存在缺失值的记录、对可能值进行插补和不处理 3种情况,
1.2 异常值分析
异常值分析是检验数据是否有录入错误以及含有不合常理的数据
(1)简单统计量分析
(2)3阿尔法原则
(3)箱型图分析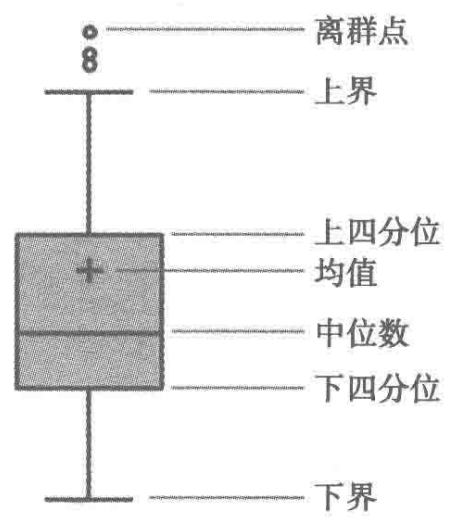
异常值通常被定义为小于QL - 1.5IQR 或 大于 QU+1.5IQR的值。
QL称为下四分位数,表示全部观察值中有四分之一的数据取值比它小;
QU称为上四分位数,表示全部观察值中有四分之一的数据取值比 它大;
IQR称为四分位数间距,是上四分位数QU与下四分位数 QL之差,其间包含了全部观察值的一半。
1.3 一致性分析
数据不一致性是指数据的矛盾性、不相容性。
二、数据特征性分析
2.1 分析分布
2.1.1 定量数据的分布分析
对于定量变量而言,选择“组数”和“组宽”是做频率分布分析时最主要的问题,一般 按照以下步骤进行。
1) 求极差。
2) 决定组距与组数。
3) 决定分点。
4 )列出频率分布表。
5)绘制频率分布直方图。
遵循的主要原则如下。
1) 各组之间必须是相互排斥的。
2)各组必须将所有的数据包含在内。
3)各组的组宽最好相等。
2.1.2 定性数据的分布分析
对于定性变量,常常根据变量的分类类型来分组,可以采用饼图和条形图来描述定性变 量的分布。
2.2 对比分析
对比分析是指把两个相互联系的指标进行比较,从数量上展示和说明研究对象规模的大 小,水平的高低,速度的快慢,以及各种关系是否协调。特别适用于指标间的横纵向比较、 时间序列的比较分析。在对比分析中,选择合适的对比标准是十分关键的步骤,只有选择合 适,才能做出客观的评价,选择不合适,评价可能得出错误的结论。
对比分析主要有两种形式:
(1)绝对数比较
(2)相对数比较
1)结构相对数
2)比例相对数
3)比较相对数
4)强度相对数
5)计划完成程度相对数
6)动态相对数
2.3 统计量分析
用统计指标对定量数据进行统计描述,常从集中趋势和离中趋势两个方面进行分析。
平均水平的指标是对个体集中趋势的度量,使用最广泛的是均值和中位数;反映变异程度的指标则是对个体离开平均水平的度量,使用较广泛的是标准差(方差)、四分位间距。
2.3.1 集中趋势度量
(1)均值
均值是所有数据的平均值。
如果求N个原始观察数据的平均数,计算公式为:
平均值: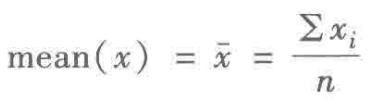
有时,为了反映在均值中不同成分所占的不同重要程度,为数据集中的每一个xi赋予wi,这就得到了加权均值的计算公式:
加权均值: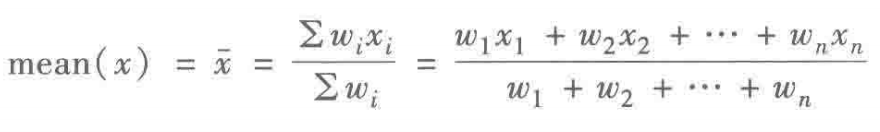
频率分布表的平均数: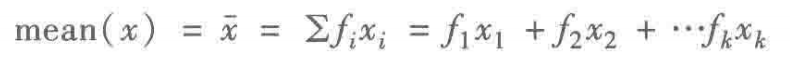

(2)中位数
中位数是将一组观察值按从小到大的顺序排列,位于中间的那个数。即在全部数据中, 小于和大于中位数的数据个数相等。
当n为奇数时:
当n为偶数时:
(3)众数
众数是指数据集中出现最频繁的值。众数并不经常用来度量定性变量的中心位置,更适 用于定性变量。众数不具有唯一性。当然,众数一般用于离散型变量而非连续型变量。
2.3.2 离中趋势度量
(1)极值
极差=最大值 - 最小值
极差对数据集的极端值非常敏感,并且忽略了位于最大值与最小值之间的数据的分布 情况。
(2)标准差
标准差度量数据偏离均值的程度,计算公式为:
(3)变异系数
变异系数度量标准差相对于均值的离中趋势,计算公式为:
变异系数主要用来比较两个或多个具有不同单位或不同波动幅度的数据集的离中趋势。
(4) 四分位数间距
四分位数包括上四分位数和下四分位数。将所有数值由小到大排列并分成四等份,处于 第一个分割点位置的数值是下四分位数,处于第二个分割点位置(中间位置)的数值是中位 数,处于第三个分割点位置的数值是上四分位数。
四分位数间距,是上四分位数与下四分位数
之差,其间包含了全部观察值的一 半。其值越大,说明数据的变异程度越大;反之,说明变异程度越小。
2.4 周期性分析
周期性分析是探索某个变量是否随着时间变化而呈现出某种周期变化趋势。时间尺度相 对较长的周期性趋势有年度周期性趋势、季节性周期趋势,相对较短的有月度周期性趋势、 周度周期性趋势,甚至更短的天、小时周期性趋势。
2.5 贡献度分析
贡献度分析又称帕累托分析,它的原理是帕累托法则,又称20/80定律。同样的投入放 在不同的地方会产生不同的效益。
2.6 相关性分析
2.6.1 直接绘制散点图
判断两个变量是否具有线性相关关系的最直观的方法是直接绘制散点图。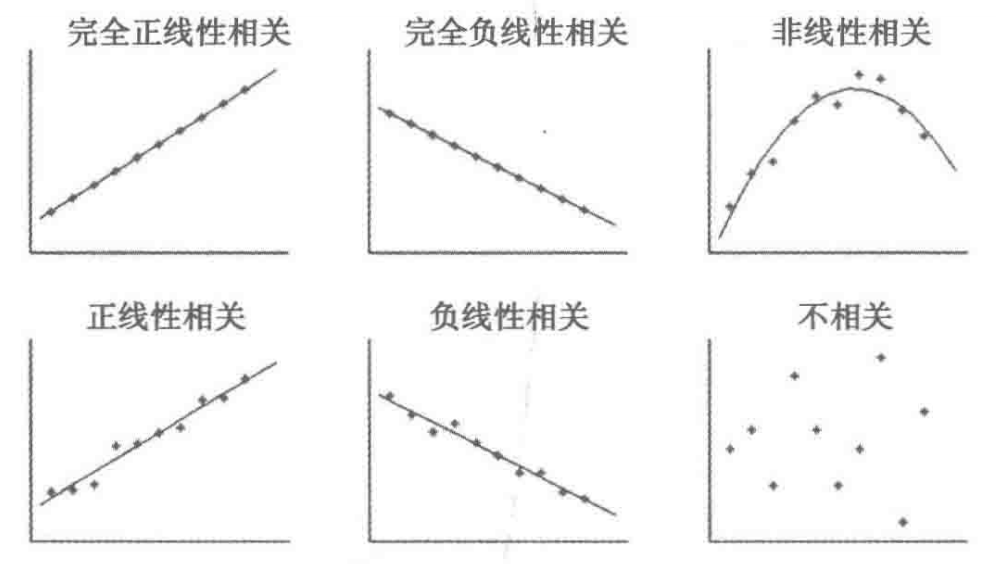
2.6.2 绘制散点图矩阵
利用散点图矩阵同时绘制各变量间的散点图,从而快速发现多个变量间的主要相关性。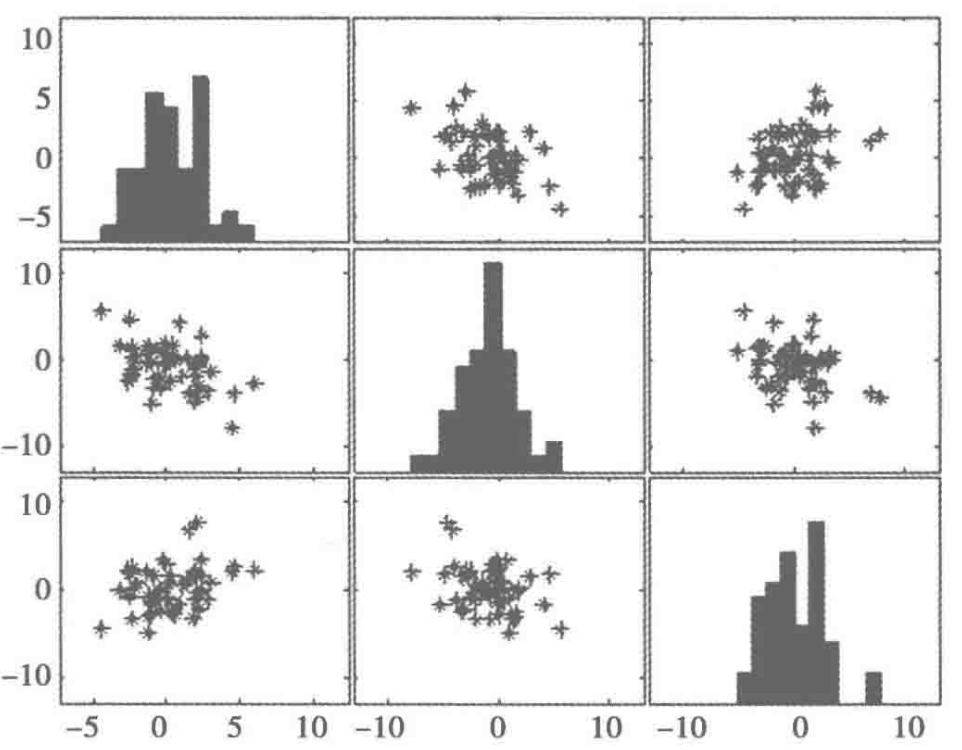
2.6.3 计算相关系数
(1) Pearson相关系数
(2)Spearman秩相关系数
Pearson线性相关系数要求连续变量的取值服从正态分布。不服从正态分布的变量、分 类或等级变量之间的关联性可采用Spearman秩相关系数,也称等级相关系数来描述。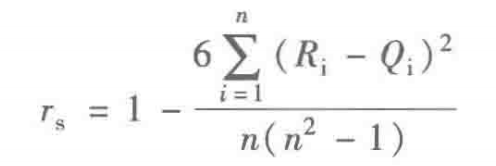
对两个变量成对的取值分别按照从小到大(或者从大到大小)顺序编秩,代表
的秩次,
代表
的秩次,
为
的秩次之差。
(3)判定系数
判定系数是相关系数的平方,用表示;用来衡量回归方程对y的解释程度。判定系数 取值范围:
。
越接近于1,表明x与y之间的相关性越强;
越接近于0,表明 两个变量之间几乎没有直线相关关系。
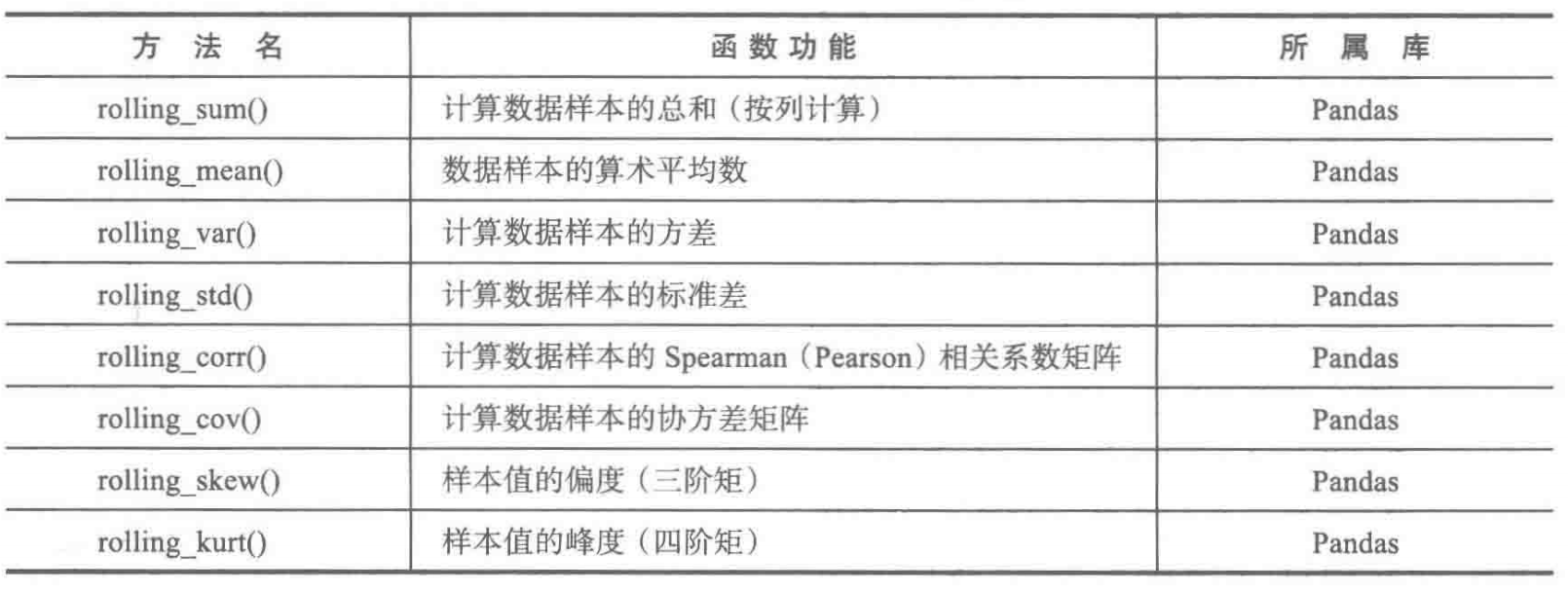
三、python主要数据探索函数
3.1 基本统计特征函数
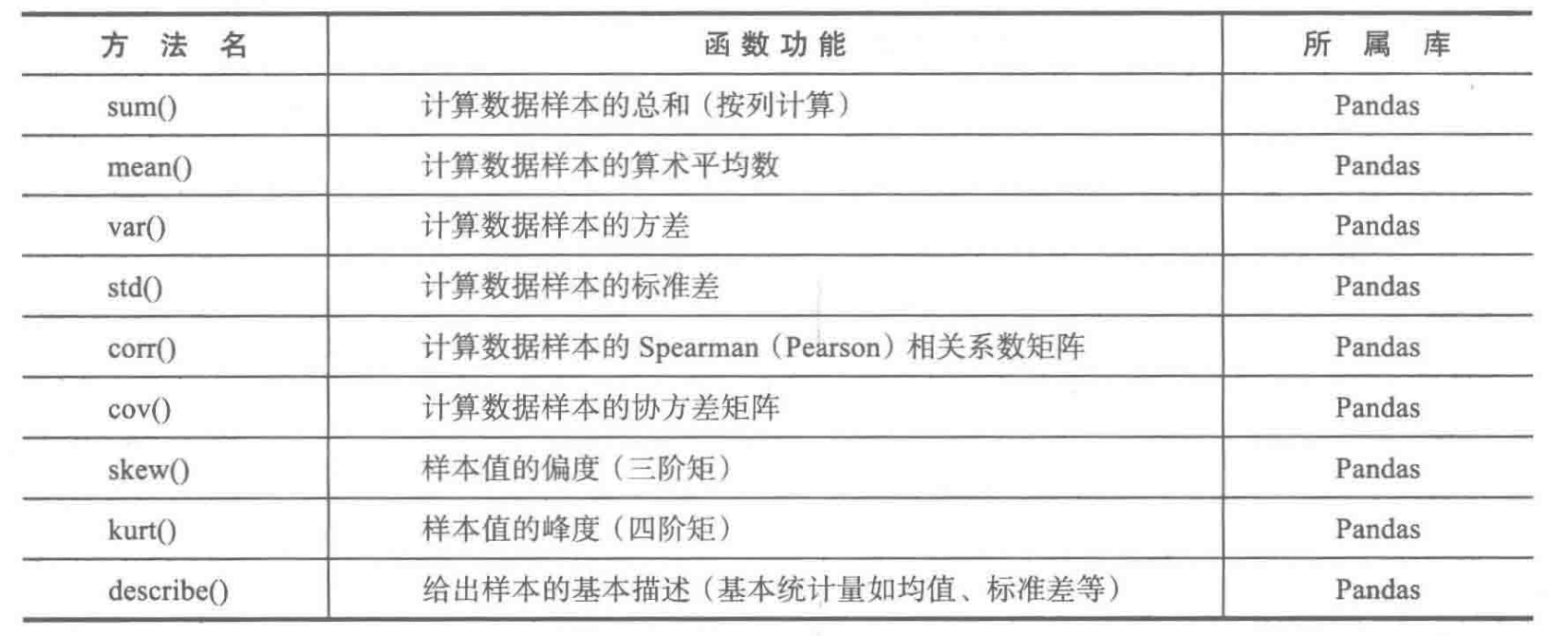
3.2扩展统计特征函数
3.3 统计作图函数