- 模型层结构
- layer(嵌入层)">1.embedding layer(嵌入层)
- 2.positional encoding(位置编码)
- 注意力机制)">3.Scaled dot-product attention(缩放的点乘注意力机制)
- 4.Multi-head attention(多头注意力)
- mask">5.Padding mask
- 6.残差连接
- 7.Layer Normalization
- 8.Position-wise Feed-Forward network
- Encoder结构
- Decoder结构
- 训练和解码
- 问题
- 参考
Transformer是一个Seq2Seq架构的模型,所以它也由Encoder与Decoder这2部分组成。但它并不是使用RNN神经网络来捕获远距离信息的,它主要采用一种自注意力机制的深度学习模型,这一机制可以按输入数据各部分重要性的不同而分配不同的权重。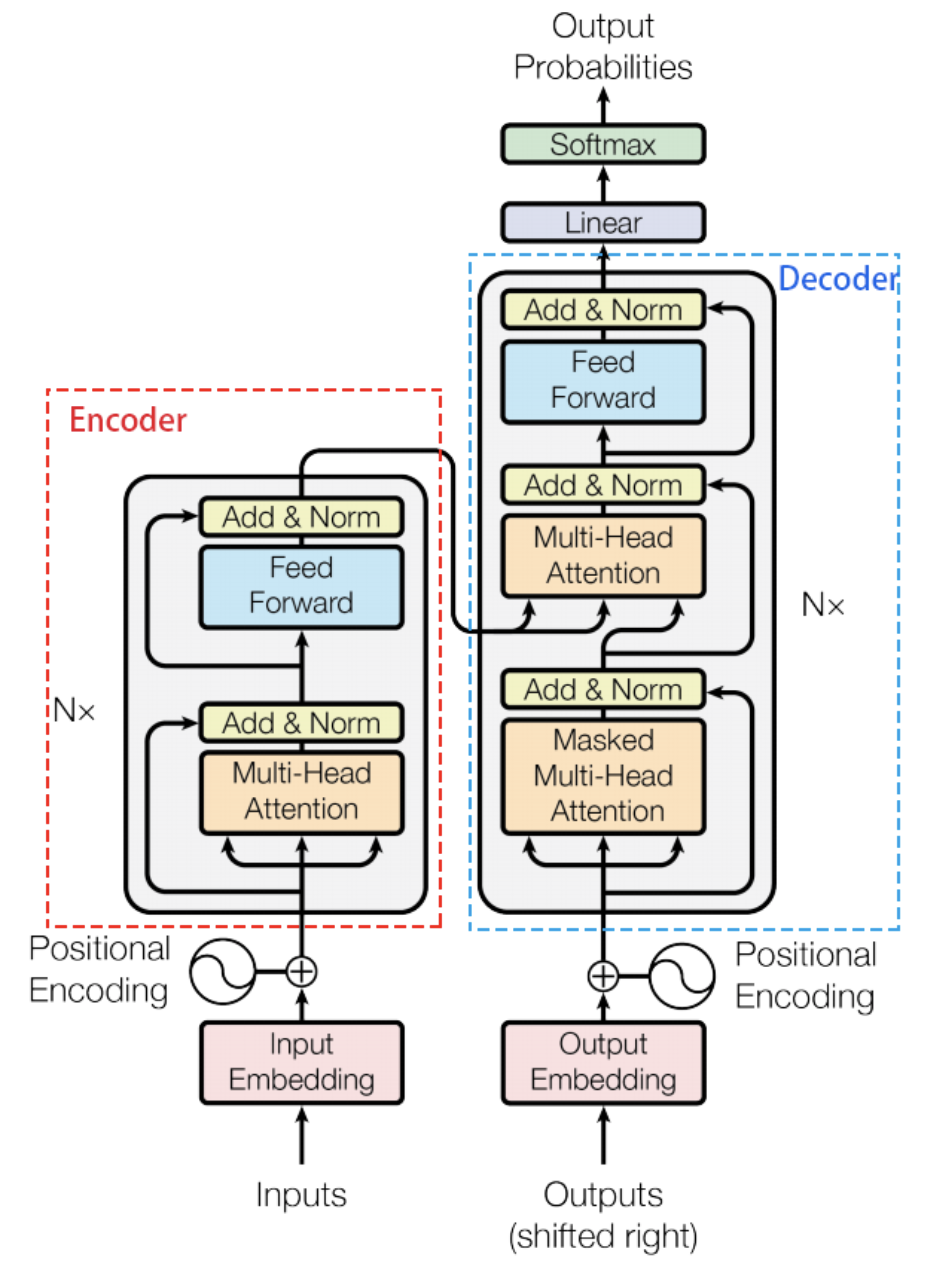
论文
代码实例分享于https://github.com/SamLynnEvans/Transformer Transformer做翻译任务
class Transformer(nn.Module):def __init__(self, src_vocab, trg_vocab, d_model, N, heads, dropout):super().__init__()self.encoder = Encoder(src_vocab, d_model, N, heads, dropout)self.decoder = Decoder(trg_vocab, d_model, N, heads, dropout)self.out = nn.Linear(d_model, trg_vocab)def forward(self, src, trg, src_mask, trg_mask):e_outputs = self.encoder(src, src_mask)d_output = self.decoder(trg, e_outputs, src_mask, trg_mask)output = self.out(d_output)return output
模型层结构
1.embedding layer(嵌入层)
d_model=512
class Embedder(nn.Module):def __init__(self, vocab_size, d_model):super().__init__()self.d_model = d_modelself.embed = nn.Embedding(vocab_size, d_model)def forward(self, x):return self.embed(x)
2.positional encoding(位置编码)
单词embedding其实是embedding + positional encoding,positional encoding和embedding的维度相同,其中pos是指当前词在句子中的位置,i是指向量中每个值的index。例如将K、V按行进行打乱,那么Attention之后的结果是一样的。但是序列信息非常重要,代表着全局的结构,因此必须将序列的token相对或者绝对position信息利用起来。
在偶数位置,使用正弦编码,在奇数位置,使用余弦编码: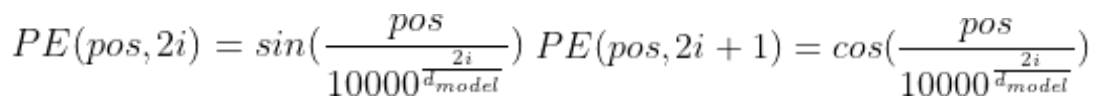
class PositionalEncoder(nn.Module):def __init__(self, d_model, max_seq_len = 200, dropout = 0.1):super().__init__()self.d_model = d_modelself.dropout = nn.Dropout(dropout)# create constant 'pe' matrix with values dependant on pos and ipe = torch.zeros(max_seq_len, d_model)for pos in range(max_seq_len):for i in range(0, d_model, 2):pe[pos, i] = math.sin(pos / (10000 ** ((2 * i)/d_model)))pe[pos, i + 1] = math.cos(pos / (10000 ** ((2 * (i + 1))/d_model)))pe = pe.unsqueeze(0)self.register_buffer('pe', pe)def forward(self, x):# make embeddings relatively larger# 这一步非必须,也可以注释掉,目的是使得embedding的值大一点,x = x * math.sqrt(self.d_model)#add constant to embeddingseq_len = x.size(1)pe = Variable(self.pe[:,:seq_len], requires_grad=False)if x.is_cuda:pe.cuda()x = x + pereturn self.dropout(x)
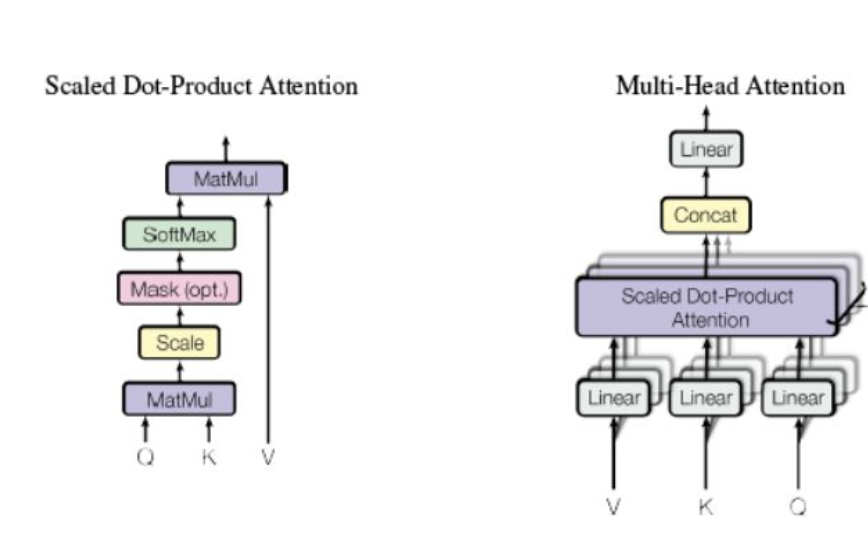
3.Scaled dot-product attention(缩放的点乘注意力机制)
输入的embedding和三个随机初始化的矩阵相乘(这个过程也可描述为经过一次线性变化)映射为维度相同的Q,K, V(映射后的维度是dq,dk,dv),然后使用self-attention(点积attention)公式计算,这三个矩阵在BP过程中会一直更新。
其中,d_k = query.size(-1)=64,d_k·h=d_model=512原因:对于很大的,点积结果增大,将softmax函数推向具有极小梯度的区域,为抵消这种影响,在Transformer中点积缩小
倍。
def attention(q, k, v, d_k, mask=None, dropout=None):scores = torch.matmul(q, k.transpose(-2, -1)) / math.sqrt(d_k)if mask is not None:mask = mask.unsqueeze(1)scores = scores.masked_fill(mask == 0, -1e9)scores = F.softmax(scores, dim=-1)if dropout is not None:scores = dropout(scores)output = torch.matmul(scores, v)return output
4.Multi-head attention(多头注意力)
multi-head attention是初始化多组Q、K、V的矩阵,这里的多头一般是指要进行h=8次,头之间参数不共享,即每次QKV进行线性变化的W都不一样,然后进行h=8次缩放点积注意力机制,tranformer最后得到的结果是8个矩阵,拼接后再映射到输出维度。结合代码。
class MultiHeadAttention(nn.Module):def __init__(self, heads, d_model, dropout = 0.1):super().__init__()self.d_model = d_modelself.d_k = d_model // headsself.h = headsself.q_linear = nn.Linear(d_model, d_model)self.v_linear = nn.Linear(d_model, d_model)self.k_linear = nn.Linear(d_model, d_model)self.dropout = nn.Dropout(dropout)self.out = nn.Linear(d_model, d_model)def forward(self, q, k, v, mask=None):bs = q.size(0)# perform linear operation and split into N headsk = self.k_linear(k).view(bs, -1, self.h, self.d_k)q = self.q_linear(q).view(bs, -1, self.h, self.d_k)v = self.v_linear(v).view(bs, -1, self.h, self.d_k)# transpose to get dimensions bs * N * sl * d_modelk = k.transpose(1,2)q = q.transpose(1,2)v = v.transpose(1,2)# calculate attention using function we will define nextscores = attention(q, k, v, self.d_k, mask, self.dropout)# concatenate heads and put through final linear layerconcat = scores.transpose(1,2).contiguous().view(bs, -1, self.d_model)output = self.out(concat)return output
5.Padding mask
padding mask 在所有的 scaled dot-product attention 里面都需要用到,因为文本的长度不同,所以我们会在处理时对其进行padding。但是注意padding是将这些位置设置为非常大的负数,这样经过softmax后的概率接近0。这么做的目的是在进行attention机制时,注意力不应该放在padding的部分。
6.残差连接
残差模块X + self-attention(X),即X经过self-attention后的结果再加上输入X,目的是为了反向传播时不会梯度消失,防止网络退化。
7.Layer Normalization
Normalization有很多种,但是它们都有一个共同的目的,那就是把输入转化成均值为0方差为1的数据。BN是在batch上计算均值和方差,而LN则是对针对同一层的所有神经元做归一化;
我们再回想下BatchNormalization,其实它是在每个神经元上对batch_size个数据做归一化,每个神经元的均值和方差均不相同。而LayerNormalization则是对所有神经元做一个归一化,这就跟batch_size无关了。哪怕batch_size为1,这里的均值和方差只和神经元的个数有关系。变长的样本,BN无法处理,BN的缺点(batch_size 和样本变长特征影响)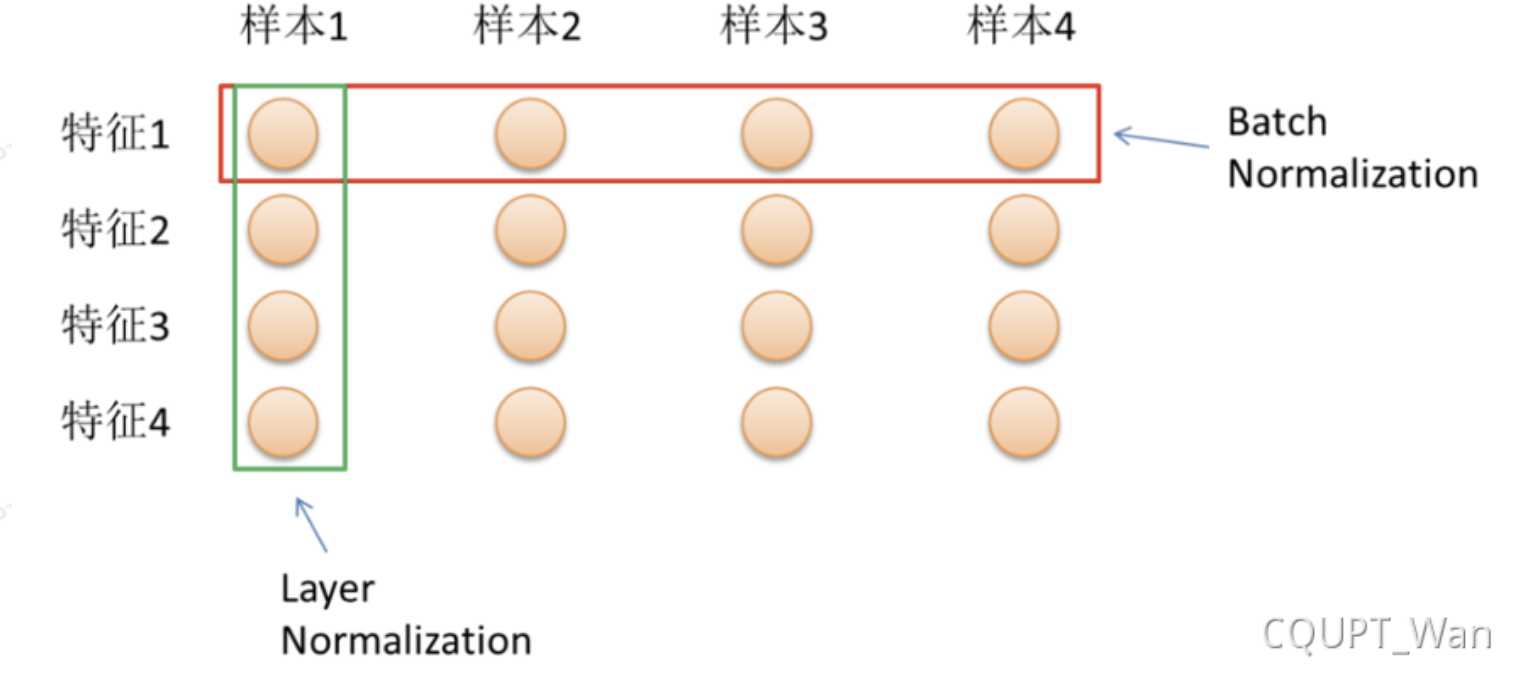
class Norm(nn.Module):def __init__(self, d_model, eps = 1e-6):super().__init__()self.size = d_model# create two learnable parameters to calibrate normalisationself.alpha = nn.Parameter(torch.ones(self.size))self.bias = nn.Parameter(torch.zeros(self.size))self.eps = epsdef forward(self, x):norm = self.alpha * (x - x.mean(dim=-1, keepdim=True)) \/ (x.std(dim=-1, keepdim=True) + self.eps) + self.biasreturn norm
8.Position-wise Feed-Forward network
Feed Forward 层比较简单,是一个两层的全连接层,第一层的激活函数为 Relu,第二层不使用激活函数。为什么需要前馈。
class FeedForward(nn.Module):def __init__(self, d_model, d_ff=2048, dropout = 0.1):super().__init__()# We set d_ff as a default to 2048self.linear_1 = nn.Linear(d_model, d_ff)self.dropout = nn.Dropout(dropout)self.linear_2 = nn.Linear(d_ff, d_model)def forward(self, x):x = self.dropout(F.relu(self.linear_1(x)))x = self.linear_2(x)return x
Encoder结构
Encoder由N = 6 个完全相同的层堆叠而成。每一层都有两个子层。第一个子层是一个multi-head self-attention机制,第二个子层是一个简单的、位置完全连接的前馈网络。我们对每个子层再采用一个残差连接,接着进行层标准化。也就是说,每个子层的输出是LayerNorm(x + Sublayer(x)),其中Sublayer(x) 是由子层本身实现的函数。为了方便这些残差连接,模型中的所有子层以及嵌入层产生的输出维度都为dmodel = 512。
class Encoder(nn.Module):def __init__(self, vocab_size, d_model, N, heads, dropout):super().__init__()self.N = Nself.embed = Embedder(vocab_size, d_model)self.pe = PositionalEncoder(d_model, dropout=dropout)self.layers = get_clones(EncoderLayer(d_model, heads, dropout), N)self.norm = Norm(d_model)def forward(self, src, mask):x = self.embed(src)x = self.pe(x)for i in range(self.N):x = self.layers[i](x, mask)return self.norm(x)def get_clones(module, N):return nn.ModuleList([copy.deepcopy(module) for i in range(N)])
encoder 结构 emb+positionemb , (归一化),多头注意力,残差+x,接归一化,输入到前馈网络,残差。
论文中是先残差再归一化,但是在 http://nlp.seas.harvard.edu/2018/04/03/attention.html#encoder中的SublayerConnection是先归一化,后残差的。论文中应该是先Add再Nrom
class EncoderLayer(nn.Module):def __init__(self, d_model, heads, dropout=0.1):super().__init__()self.norm_1 = Norm(d_model)self.norm_2 = Norm(d_model)self.attn = MultiHeadAttention(heads, d_model, dropout=dropout)self.ff = FeedForward(d_model, dropout=dropout)self.dropout_1 = nn.Dropout(dropout)self.dropout_2 = nn.Dropout(dropout)def forward(self, x, mask):x2 = self.norm_1(x)x = x + self.dropout_1(self.attn(x2,x2,x2,mask))x2 = self.norm_2(x)x = x + self.dropout_2(self.ff(x2))return x
Decoder结构
解码器同样由N = 6 个完全相同的层堆叠而成。 除了每个编码器层中的两个子层之外,解码器还插入第三个子层,该层对Encoder堆栈的输出执行multi-head attention。 与编码器类似,我们在每个子层再采用残差连接,然后进行层标准化。我们还修改解码器堆栈中的self-attention子层,以防止位置关注到后面的位置。这种掩码结合将输出嵌入偏移一个位置,确保对当前位置的预测 i只能依赖小于当前位置的已知输出。
class Decoder(nn.Module):def __init__(self, vocab_size, d_model, N, heads, dropout):super().__init__()self.N = Nself.embed = Embedder(vocab_size, d_model)self.pe = PositionalEncoder(d_model, dropout=dropout)self.layers = get_clones(DecoderLayer(d_model, heads, dropout), N)self.norm = Norm(d_model)def forward(self, trg, e_outputs, src_mask, trg_mask):x = self.embed(trg)x = self.pe(x)for i in range(self.N):x = self.layers[i](x, e_outputs, src_mask, trg_mask)return self.norm(x)
# build a decoder layer with two multi-head attention layers and# one feed-forward layerclass DecoderLayer(nn.Module):def __init__(self, d_model, heads, dropout=0.1):super().__init__()self.norm_1 = Norm(d_model)self.norm_2 = Norm(d_model)self.norm_3 = Norm(d_model)self.dropout_1 = nn.Dropout(dropout)self.dropout_2 = nn.Dropout(dropout)self.dropout_3 = nn.Dropout(dropout)self.attn_1 = MultiHeadAttention(heads, d_model, dropout=dropout)self.attn_2 = MultiHeadAttention(heads, d_model, dropout=dropout)self.ff = FeedForward(d_model, dropout=dropout)def forward(self, x, e_outputs, src_mask, trg_mask):x2 = self.norm_1(x)x = x + self.dropout_1(self.attn_1(x2, x2, x2, trg_mask))x2 = self.norm_2(x)x = x + self.dropout_2(self.attn_2(x2, e_outputs, e_outputs, \src_mask))x2 = self.norm_3(x)x = x + self.dropout_3(self.ff(x2))return x
1.sequence mask
sequence mask 是为了使得 decoder 不能看见未来的信息。也就是对于一个序列,在 time_step 为 t 的时刻,我们的解码输出应该只能依赖于 t 时刻之前的输出,而不能依赖 t 之后的输出。因此我们需要想一个办法,把 t 之后的信息给隐藏起来。
那么具体怎么做呢?也很简单:产生一个上三角矩阵,上三角的值全为0。把这个矩阵作用在每一个序列上,就可以达到我们的目的。
对于 decoder 的 self-attention,里面使用到的 scaled dot-product attention,同时需要padding mask 和 sequence mask 作为 attn_mask,具体实现就是两个mask相加作为attn_mask。
其他情况,attn_mask 一律等于 padding mask。
训练和解码
训练
def train_model(model, opt):print("training model...")model.train()start = time.time()if opt.checkpoint > 0:cptime = time.time()for epoch in range(opt.epochs):total_loss = 0if opt.floyd is False:print(" %dm: epoch %d [%s] %d%% loss = %s" % \((time.time() - start) // 60, epoch + 1, "".join(' ' * 20), 0, '...'), end='\r')if opt.checkpoint > 0:torch.save(model.state_dict(), 'weights/model_weights')for i, batch in enumerate(opt.train):src = batch.src.transpose(0, 1)trg = batch.trg.transpose(0, 1)trg_input = trg[:, :-1]src_mask, trg_mask = create_masks(src, trg_input, opt)preds = model(src, trg_input, src_mask, trg_mask)ys = trg[:, 1:].contiguous().view(-1)opt.optimizer.zero_grad()print(src.shape) #torch.Size([1, 28])print(src_mask.shape) #torch.Size([1, 1, 28])print(src_mask)print(trg.shape) #torch.Size([1, 34])print(trg_mask.shape) #torch.Size([1, 33, 33])print(trg_mask)print(preds.view(-1, preds.size(-1)).shape, ys.shape) #torch.Size([33, 663]) torch.Size([33])loss = F.cross_entropy(preds.view(-1, preds.size(-1)), ys, ignore_index=opt.trg_pad)loss.backward()opt.optimizer.step()if opt.SGDR == True:opt.sched.step()total_loss += loss.item()if (i + 1) % opt.printevery == 0:p = int(100 * (i + 1) / opt.train_len)avg_loss = total_loss / opt.printeveryif opt.floyd is False:print(" %dm: epoch %d [%s%s] %d%% loss = %.3f" % \((time.time() - start) // 60, epoch + 1, "".join('#' * (p // 5)),"".join(' ' * (20 - (p // 5))), p, avg_loss), end='\r')else:print(" %dm: epoch %d [%s%s] %d%% loss = %.3f" % \((time.time() - start) // 60, epoch + 1, "".join('#' * (p // 5)),"".join(' ' * (20 - (p // 5))), p, avg_loss))total_loss = 0if opt.checkpoint > 0 and ((time.time() - cptime) // 60) // opt.checkpoint >= 1:torch.save(model.state_dict(), 'weights/model_weights')cptime = time.time()print("%dm: epoch %d [%s%s] %d%% loss = %.3f\nepoch %d complete, loss = %.03f" % \((time.time() - start) // 60, epoch + 1, "".join('#' * (100 // 5)), "".join(' ' * (20 - (100 // 5))), 100,avg_loss, epoch + 1, avg_loss))
src.shape:torch.Size([1, 26])src_mask.shape:torch.Size([1, 1, 26])src_mask:tensor([[[True, True, True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True, True, True,True, True, True, True]]])tgr.shape:torch.Size([1, 31])tgr_mask.shape:torch.Size([1, 30, 30])tgr_mask:tensor([[[ True, False, False, False, False, False, False, False, False, False,False, False, False, False, False, False, False, False, False, False,False, False, False, False, False, False, False, False, False, False],[ True, True, False, False, False, False, False, False, False, False,False, False, False, False, False, False, False, False, False, False,False, False, False, False, False, False, False, False, False, False],[ True, True, True, False, False, False, False, False, False, False,False, False, False, False, False, False, False, False, False, False,False, False, False, False, False, False, False, False, False, False],...[ True, True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True, False],[ True, True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True, True,True, True, True, True, True, True, True, True, True, True]]])torch.Size([30, 663]) torch.Size([30])
训练解码
#输入src_seqsrc_seq: i see.sentence: ['i', 'see', '.']indexed: [8, 192, 2]beam_search 找到最优路径
- 输入:encoder的输出 & 对应i-1位置decoder的输出。
- 输出:对应i位置的输出词的概率分布
所以中间的attention不是self-attention,它的K,V来自encoder,Q来自上一位置decoder的输出。
- 解码:这里要注意一下,训练和预测是不一样的。在训练时,解码是一次全部decode出来,用上一步的ground truth来预测(mask矩阵也会改动,让解码时看不到未来的token);而预测时,因为没有ground truth了,需要一个个预测。
- 解码的区别主要是:一个是attention的输入,一个是decoder 的mask。
直到输出一个特殊符号
,表示已经完成了。对于Decoder,和Encoder一样,我们在每个Decoder的输入做词嵌入并添加上表示每个字位置的位置编码 预测解码
输入:encoder的输出 & 对应i-1位置decoder的输出。
- 输出:对应i位置的输出词的概率分布
首先tgr的第一个元素是
,直到 预测结束,每次模型输入的tgr都是将上一步的tgr 的预测结果作为输入。 如第12行所示: def beam_search(src, model, SRC, TRG, opt):# outputs是三个句子,三个句子的第一个元素是<sos>,同时预测了第二个元素,也就是目标序列的第一个词outputs, e_outputs, log_scores = init_vars(src, model, SRC, TRG, opt)# outputs:【3,80】# e_outputs:【3,3,663】# log_scores:[1, 3]print("outputs", outputs.shape) # [3,80]eos_tok = TRG.vocab.stoi['<eos>']src_mask = (src != SRC.vocab.stoi['<pad>']).unsqueeze(-2)ind = Nonefor i in range(2, opt.max_len): # 从第3个索引,也就是第二个词开始预测,trg_mask = nopeak_mask(i, opt)out = model.out(model.decoder(outputs[:, :i],e_outputs, src_mask, trg_mask)) # []out = F.softmax(out, dim=-1)print("out", out.shape) # [k, seqlength,vocab_size] #[3, 2, 663]outputs, log_scores = k_best_outputs(outputs, out, log_scores, i, opt.k)print("outputs", outputs.shape) # torch.Size([3, 80])print("log_scores",log_scores.shape)ones = (outputs == eos_tok).nonzero() # Occurrences of end symbols for all input sentences.print("ones", ones)if opt.device == 0:sentence_lengths = torch.zeros(len(outputs), dtype=torch.long).cuda()else:sentence_lengths = torch.zeros(len(outputs), dtype=torch.long)for vec in ones:i = vec[0]if sentence_lengths[i] == 0: # First end symbol has not been found yetsentence_lengths[i] = vec[1] # Position of first end symbolnum_finished_sentences = len([s for s in sentence_lengths if s > 0])# <eos>的个数等于topk 的个数,证明三个都预测完了if (outputs == eos_tok).cpu().numpy().argmax(axis=1).nonzero()[0].shape[0] == opt.k:alpha = 0.7div = 1 / (torch.tensor(((outputs == eos_tok).cpu().numpy().argmax(axis=1))).type_as(log_scores) ** alpha)_, ind = torch.max(log_scores * div, 1)ind = ind.data[0]breakif ind is None:print(eos_tok)print(outputs)print((outputs[0] == eos_tok).nonzero())length = (outputs[0] == eos_tok).nonzero()[0]return ' '.join([TRG.vocab.itos[tok] for tok in outputs[0][1:length]])else:print("res outputs", outputs)print("res nonzero", (outputs[ind] == eos_tok).nonzero())length = (outputs[ind] == eos_tok).nonzero()[0]return ' '.join([TRG.vocab.itos[tok] for tok in outputs[ind][1:length]])
问题
1.transform 的encoder和decoder的区别?
:::info 1)结构方面:encoder有两个子层,分别是多头的的自注意力网络,还有一个前馈网络,每层之间采用残差连接,然后再进行LayerNorm。decoder每个block除了编码器层中的两个子层之外,解码器还插入第三个子层,该层对Encoder堆栈的输出执行multi-head attention。
2)输入方面:decoder的时候,encoder-decoder中的attention,query 来自decoder的多层注意力输出,key和value来自encoder的输出。encoder的时候,key ,query, value 是一样的。
3)mask方面:encoder是因为文本长度不一样,padding是将超出实际长度的位置设置为非常大的负数,这样经过softmax后的概率接近0。decoder 对目标序列的self-attention,以防止位置关注到后面的位置。这种mask结合将输出嵌入偏移一个位置,确保对当前位置的预测 只能依赖小于i当前位置的已知输出。 :::2.transform 编码器和解码器中attention的区别?
:::info 在“Encoder-Decoder Attention”层,query来自上面的decoder的多头注意力层的输出,key和value来自encoder的输出。这允许Decoder中的每个位置能关注到输入序列中的所有位置。这模仿Seq2Seq模型中典型的Encoder-Decoder的attention机制。
3.Transformer为什么需要进行Multi-head Attention?
:::info 将计算结果映射到不同的子空间,使模型关注到不同方面的信息,最后再综合起来。 :::
4.为什么需要前馈?
:::info
在编码器的self-attention和前馈神经网络后分别都有,目的是
(1)防止梯度消失。
(2)解决深度学习网络的退化问题。(退化问题是指,当模型对不同的输入均给出同样的输出)
:::
5.Transformer的并行化提现在哪里?
:::info
(1)并行计算的能力。RNN系列的模型,并行计算能力很差,因为 T 时刻的计算依赖 T-1 时刻的隐层计算结果,而 T-1 时刻的计算依赖 T-2 时刻的隐层计算结果,如此下去就形成了序列依赖关系。
(2)特征提取能力更好。
:::
6.Transformer和RNN,CNN的不同?
:::info
(1)它是直接进行的长距离依赖特征的获取的,不像RNN需要通过隐层节点序列往后传,也不像CNN(局部编码)需要通过增加网络深度来捕获远距离特征。
(2)RNN系列的模型,并行计算能力很差,Transformer并性能力
(3)复杂度,当句子长度和词嵌入维度差不多的时候,复杂度差不多,
:::
- 每一层的计算复杂度
- 能够被并行的计算,用需要的最少的顺序操作的数量来衡量
- 网络中long-range dependencies的path length,在处理序列信息的任务中很重要的在于学习long-range dependencies。影响学习长距离依赖的关键点在于前向/后向信息需要传播的步长,输入和输出序列中路径越短,那么就越容易学习long-range dependencies。因此我们比较三种网络中任何输入和输出之间的最长path length
7.self-attention时间复杂度
8.全连接网络和自注意力区别
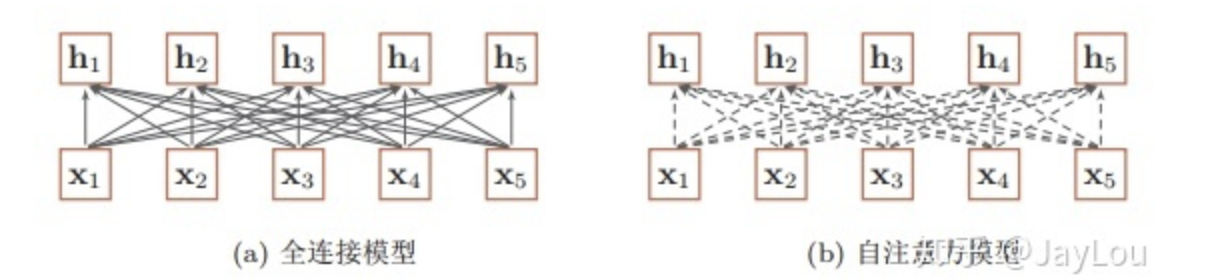 :::info
(1)全连接模型节点之间是可学习的权重,注意力模型节点之间动态生成的权重。
:::info
(1)全连接模型节点之间是可学习的权重,注意力模型节点之间动态生成的权重。
(2)全连接网络虽然是一种非常直接的建模远距离依赖的模型, 但是无法处理变长的输入序列。不同的输入长度,其连接权重的大小也是不同的。由于自注意力模型的权重是动态生成的,因此可以处理变长的信息序列。
:::
9.什么是transformer
:::info Transformer是一个Seq2Seq架构的模型,所以它也由Encoder与Decoder这2部分组成。但它并不是使用RNN神经网络来捕获远距离信息的,它主要采用一种自注意力机制的深度学习模型,这一机制可以按输入数据各部分重要性的不同而分配不同的权重。 :::
10.transformer 的结构
:::info 分别描述encoder 和decoder的结构 :::
11.transformer attention的时候为啥要除以根号D
:::info
至于attention后的权重为啥要除以 ,作者在论文中的解释是点积后的结果大小是跟维度成正比的,所以经过softmax以后,梯度就会变很小,除以
后可以让attention的权重分布方差为1,而不是
。
具体细节(简而言之就是softmax如果某个输入太大的话就会使得权重太接近于1,梯度很小)
transformer中的attention为什么scaled?1733 赞同 · 53 评论回答
:::
参考
https://www.yuque.com/kaiba-20hbu/aev2fm/yexiqv
https://www.yuque.com/kaiba-20hbu/aev2fm/yexiqv#so66x
哈弗团队 pytorch版本代码 http://nlp.seas.harvard.edu/2018/04/03/attention.html



