实现

python版本

class Trie:
    # word_end = -1
    def __init__(self):
        """
        Initialize your data structure here.
        """
        self.root = {}
        self.word_end = -1
    def insert(self, word):
        """
        Inserts a word into the trie.
        :type word: str
        :rtype: void
        """
        curNode = self.root
        for c in word:
            if not c in curNode:
                curNode[c] = {}
            curNode = curNode[c]
        curNode[self.word_end] = True
    def search(self, word):
        """
        Returns if the word is in the trie.
        :type word: str
        :rtype: bool
        """
        curNode = self.root
        for c in word:
            if not c in curNode:
                return False
            curNode = curNode[c]
            # Doesn't end here
        if self.word_end not in curNode:
            return False
        return True
    def startsWith(self, prefix):
        """
        Returns if there is any word in the trie that starts with the given prefix.
        :type prefix: str
        :rtype: bool
        """
        curNode = self.root
        for c in prefix:
            if not c in curNode:
                return False
            curNode = curNode[c]
        return True
        # Your Trie object will be instantiated and called as such:
        # obj = Trie()
        # obj.insert(word)
        # param_2 = obj.search(word)
        # param_3 = obj.startsWith(prefix)

Trie树和其他几种树的比较

二叉搜索树相比

二叉搜索树又叫二叉排序树，Trie 树是N 叉树，其一个重要性质是左节点小于根节点的值，右节点都大于根节点的值，Trie 更适合字符串的场景，如果处理浮点数的话，就可能导致整个 Trie 树巨长无比，节点可读性也非常差。

Hash 表相比

省内存，解决Hash 表键冲突的问题。
hash 精确查找，trie 树用于解决前缀检索的场景。
但是在精确查找的场景，hash要比trie快很多。 :::info hash 精确查找可以做到O(1)，模糊查找需要进行匹配，时间复杂度是O(mn)，m是词的个数，平均水平是o(n) :::

后缀树相比

后缀树：就是把一串字符的所有后缀保存并且压缩的字典树，
前缀树：不同字符串的相同前缀只保存一份。
在算法题中许多关于 “前缀子串”问题上，我们经常使用 Trie 树来求解，但是如果问题仅仅涉及 “子串”，往往选用后缀树；

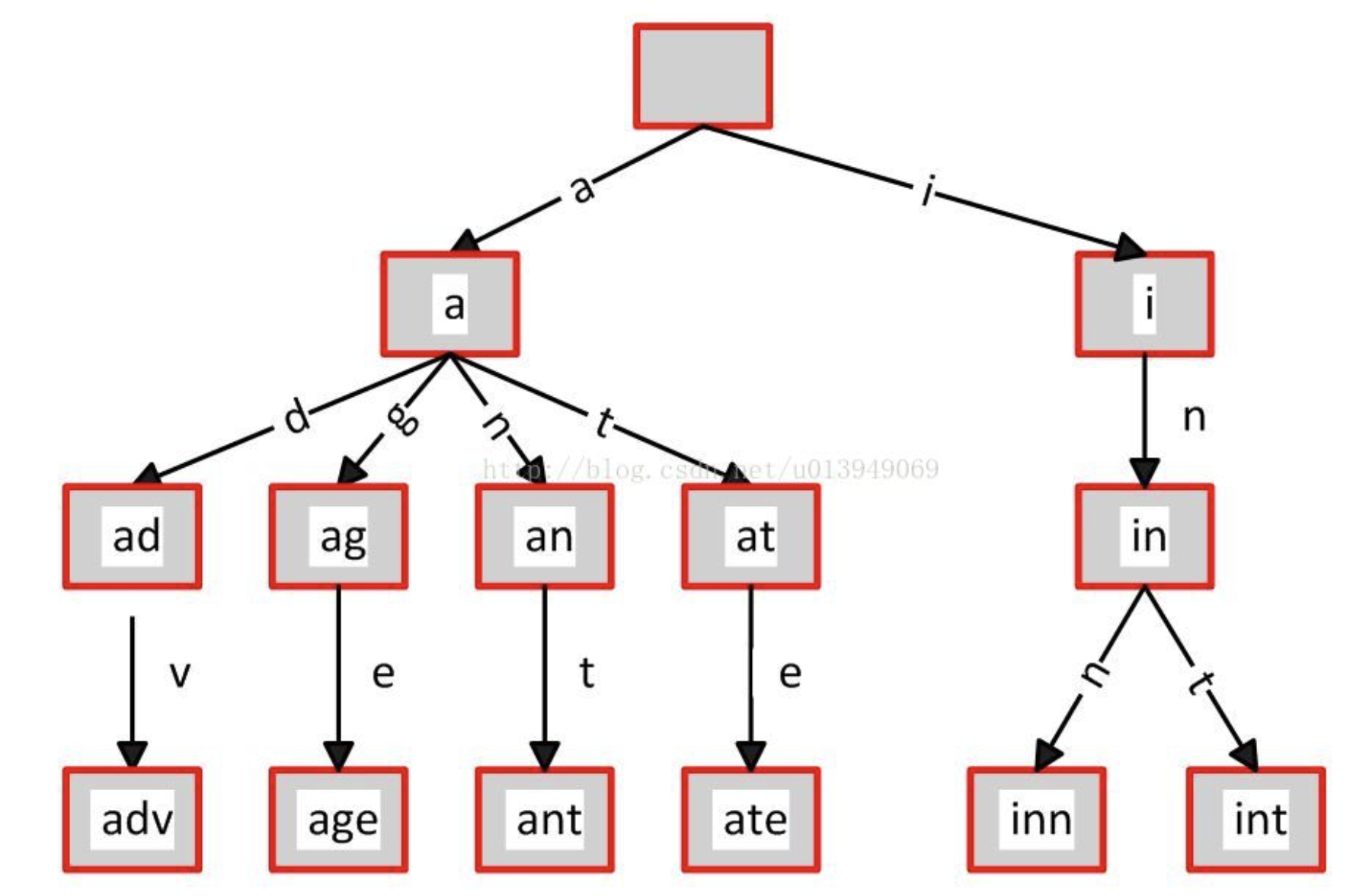
后缀树前缀树
比如：查找某个字符串s1是否在另外一个字符串s2中。这个很简单，如果s1在字符串s2中，那么s1必定是s2中某个后缀串的前缀。
法1:遍历S2，如果S2中的字符开始和S1 中的字符一样，就开始计数，如果不一样就重新开始计数，最后判断最长的计数和S1 的长度是不是一样。
法2:例如S2: banana，查找S1:nan是否在S2中,则S1(nan)必然是S2(banana)的后缀之一nana的前缀，只需要查找叶子结点就行。

应用场景

1.字符串检索

事先将已知的一些字符串（字典）的有关信息保存到trie树里，查找另外一些未知字符串是否出现过或者出现频率。

敏感词检测，有敏感词词表。
1000万字符串，其中有些是重复的，需要把重复的全部去掉，保留没有重复的字符串。

2.词频统计
有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。
一个文本文件，大约有一万行，每行一个词，要求统计出其中最频繁出现的前10个词，请给出思想，给出时间复杂度分析。

若无内存限制：Trie + “k-大/小根堆”（k为要找到的数目）。
若有内存限制：先hash分段再对每一个段用hash（另一个hash函数）统计词频，再要么利用归并排序的某些特性（如partial_sort），要么利用某使用外存的方法。

3.文本预测-字符串公共前缀

自动补全

4.排序
Trie树是一棵多叉树，只要先序遍历整棵树，输出相应的字符串便是按字典序排序的结果。
比如给你N 个互不相同的仅由一个单词构成的英文名，让你将它们按字典序从小到大排序输出。

Trie树改进
分支压缩：对于稳定的 Trie 树，基本上都是查找和读取操作，完全可以把一些分支进行压缩。例如，前图中最右侧分支的 inn 可以直接压缩成一个节点 “inn”，而不需要作为一棵常规的子树存在。Radix 树就是根据这个原理来解决 Trie 树过深问题的。

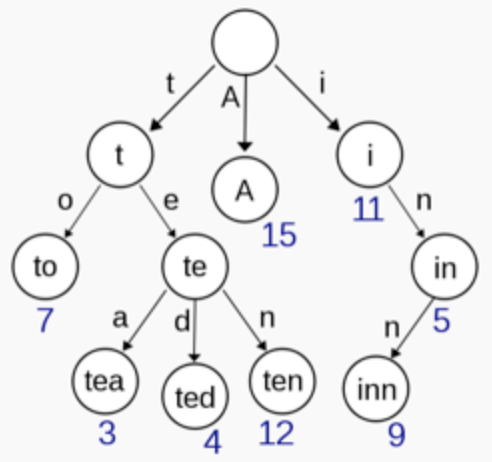
节点映射表：这种方式也是在 Trie 树的节点可能已经几乎完全确定的情况下采用的，针对 Trie 树中节点的每一个状态，如果状态总数重复很多的话，通过一个元素为数字的多维数组（比如 Triple Array Trie）来表示，这样存储 Trie 树本身的空间开销会小一些，虽说引入了一张额外的映射表。😥
变种树
AC树
AC 自动机，是在 Trie 树的基础上进行优化，当匹配失败时，跳转到指向与当前字符将主串重新匹配的位置向后多移动几位。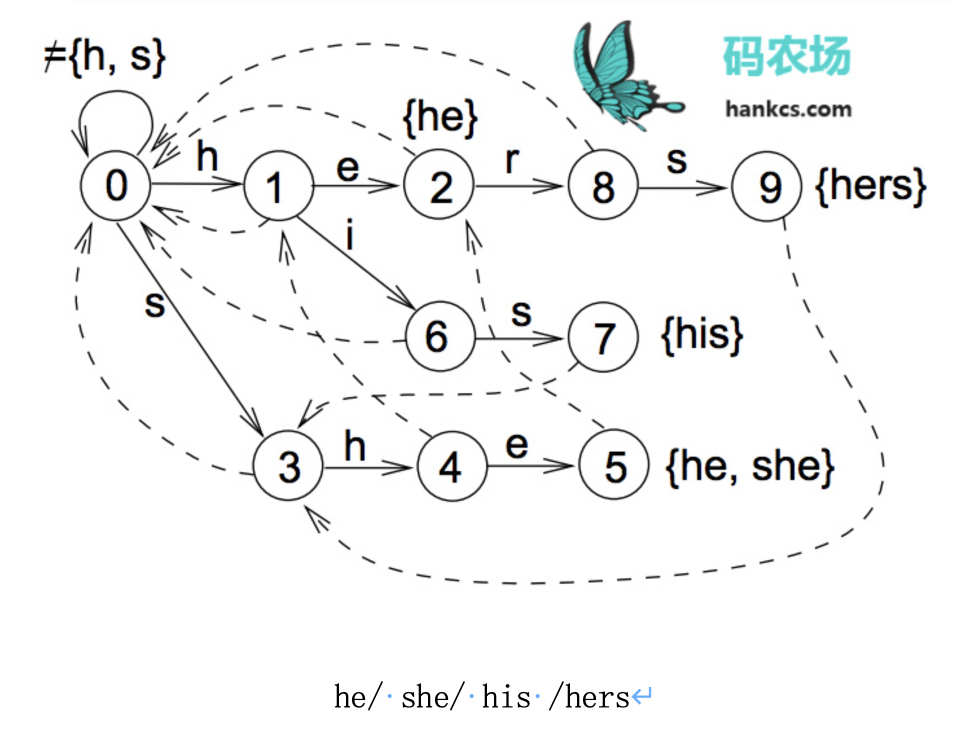

匹配过程：
假设待匹配文本为”hisshers”，那么状态转移为：0->1->6->7->3 ->0->3->4->5->2 ->8->9，文本仅扫描了一遍，依次输出结果”his”、”she”、”he”、”he”、”hers”。
比如一个字符串shers，she模式是含有hers模式的前缀he，当在状态5匹配失效时跳转到状态2继续匹配。Ac 树比一般字典树高效的一个关键点。代码就是每个树多了一个node指针。
golang版本
```go import ( “unicode/utf8” )

type node struct { next map[rune]node fail node wordLength int }

type Trie struct { root *node nodeCount int }

// New returns an empty aca. func New() Trie { return &Trie{root: &node{}, nodeCount: 1} } func (T Trie) InitRootNode() { n := new(node) n.fail = nil n.next = make(map[rune]*node) n.wordLength = 0

}

// Add adds a new word to aca. // After Add, and before Find, // MUST Build. func (T Trie) Add(word string) { n := T.root for _, r := range word { //hers // fmt.Println(“r”,r) if n.next == nil { n.next = make(map[rune]node) } if n.next[r] == nil { n.next[r] = &node{} T.nodeCount++ } n = n.next[r] } n.wordLength = len(word) }

// Del delete a word from aca. // After Del, and before Find, // MUST Build. func (T Trie) Del(word string) { rs := []rune(word) //rs:=word stack := make([]node, len(rs)) n := T.root

for i, r := range rs {
    if n.next[r] == nil {
        return
    }
    stack[i] = n
    n = n.next[r]
}
// if it is NOT the leaf node
if len(n.next) > 0 {
    n.wordLength = 0
    return
}
// if it is the leaf node
for i := len(rs) - 1; i >= 0; i-- {
    stack[i].next[rs[i]].next = nil
    stack[i].next[rs[i]].fail = nil
    delete(stack[i].next, rs[i])
    T.nodeCount--
    if len(stack[i].next) > 0 ||
        stack[i].wordLength > 0 {
        return
    }
}

}

// BuildTrie for Agentids, It MUST be called before Find. func (T *Trie) BuildTrie(dictionary [][]byte) { for _, line := range dictionary { if len(line) <= 0 { continue } T.Add(string(line)) } T.Build() }

//Build BuildTrie func (T Trie) Build() { // allocate enough memory as a queue q := append(make([]node, 0, T.nodeCount), T.root) for len(q) > 0 { n := q[0] q = q[1:]

    for r, c := range n.next {
        q = append(q, c)
        p := n.fail //n:h
        for p != nil {
            // ATTENTION: nil map cannot be writen
            // but CAN BE READ!!!
            if p.next[r] != nil {   //fail 指针指针的r指针也是存在,fail 指针进行链接，链接完跳出循环
                c.fail = p.next[r] //r:e
                break
            }
            p = p.fail             //指向自己的fail指针
        }
        if p == nil {
            c.fail = T.root     //fail指针指向root
        }
    }
}

}

func (T *Trie) find(s string, cb func(start, end int)) { n := T.root for i, r := range s { for n.next[r] == nil && n != T.root { n = n.fail } n = n.next[r] if n == nil { n = T.root continue }

    end := i + utf8.RuneLen(r)
    for t := n; t != T.root; t = t.fail {
        if t.wordLength > 0 {
            cb(end-t.wordLength, end)
        }
    }
}

}

// Find finds all the words contains in s. // The results may duplicated. // It is caller’s responsibility to make results unique. func (T *Trie) Find(s string) (words []string) {

T.find(s, func(start, end int) {
    //charactor, length := utf8.DecodeRune(s[start:end])
    words = append(words, s[start:end])
})
return

}

```

问题

Trie 树一般用于什么场景？

:::info Trie树，是一种树形结构，用于保存关联数组。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串）。 :::

Trie 树有哪些优点？

:::info

最坏情况时间复杂度比hash表好。
没有冲突，除非一个key对应多个值（除key外的其他信息）。
自带排序功能（类似Radix Sort），中序遍历trie可以得到排序。 :::

Trie 树有哪些缺点？
:::info
虽然不同单词共享前缀，但其实trie是一个以空间换时间的算法。其每一个字符都可能包含至多字符集大小数目的指针。
如果数据存储在外部存储器等较慢位置，Trie会较hash速度慢（hash访问O(1)次外存，Trie访问O(树高)）。
长的浮点数等会让链变得很长。可用bitwise trie改进或者直接用二叉排序树就好了。 :::
时间复杂度？
:::info 创建时间复杂度为O(n)
插入和搜索的代价是O（n）
查询时间复杂度是O(logn)，查询时间复杂度最坏情况下是O(n)，n是字符串的长度 :::

Trie 树

实现

python版本

Trie树和其他几种树的比较

二叉搜索树相比

Hash 表相比

后缀树相比

应用场景

1.字符串检索

2.词频统计

3.文本预测-字符串公共前缀

4.排序

Trie树改进

变种树

AC树

golang版本

问题

Trie 树一般用于什么场景？

Trie 树有哪些优点？

Trie 树有哪些缺点？

时间复杂度？