• 曲线拟合的理论在数值分析中由详细介绍

    多项式拟合方法

  • a = polyfit(x0, y0, m) x0,y0为要拟合的数据，m为拟合多项式的次数，输出的a为次数从高到低的系数

  • y = polyval(a, x) 多项式在x处的值

    例1

  • 某乡镇企业1990-1996 年的生产利润如下表

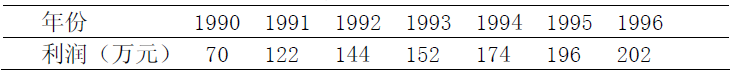
image.png
试预测1997 年和1998 年的利润。

matlab两种方法求解

  1. x0=[1990  1991  1992  1993  1994  1995  1996];
  2. y0=[70   122   144   152   174   196   202];
  3. %plot(x0,y0,'*') #先做出散点图，由散点图可知拟合线性函数
  5. %拟合多项式的方法
  6. a=polyfit(x0,y0,1)
  7. y1=polyval(a,x0)
  9. %拟合任意一元函数的方法
  10. syms x %定义变量t
  11. f=fittype('a1*x + a0','independent','x','coefficients',{'a1','a0'})%自定义拟合函数，可以是知数函数等
  12. cfun=fit(x0',y0',f) %根据自定义的函数拟合x,y;注意：x,y必须是列向量
  13. y1=cfun(x0);
  15. %作图
  16. plot(x0,y1,x0,y0,'r*')
  18. >>> y97=polyval(a,1997)
  19. >>> y98=polyval(a,1998)
  21. >>> y97=cfun(1997)
  22. >>> y98=cfun(1998)

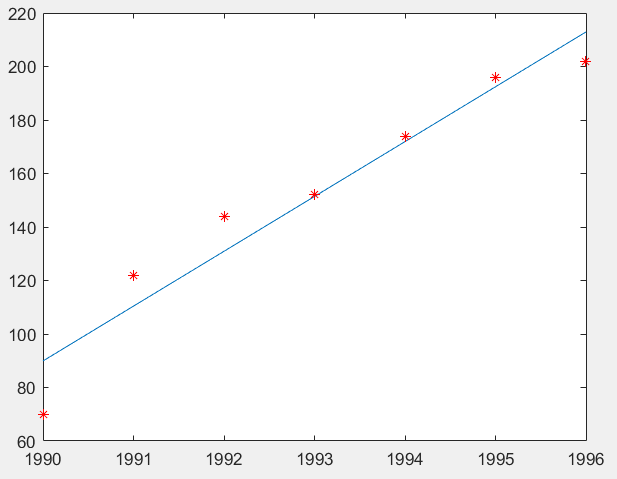
image.png

python两种方法求解

  1. import numpy as np
  2. import matplotlib.pyplot as plt
  3. from scipy.optimize import curve_fit#拟合
  5. x0 = np.array([1990, 1991, 1992, 1993, 1994, 1995, 1996])
  6. y0 = np.array([70, 122, 144, 152, 174, 196, 202])
  8. #拟合多项式
  9. coefficients= np.polyfit(x0, y0, 1)#拟合一次函数得到的系数
  10. p1=np.poly1d(coefficients)#合成的一次多项式
  11. y1=p1(x0)#拟合的y值
  13. #拟合任意一元函数的方法
  14. fun = lambda x, a0, a1: a1*x + a0 #自定义函数，可以是指数函数等别的类型函数
  15. a,pcov=curve_fit(fun, x0, y0)#a是最小二乘法得到的系数，pcov是参数的估计协方差
  16. y1=fun(x0,a[0],a[1])
  18. #作图
  19. plt.figure()
  20. plt.plot(x0, y0, '*', label='original values')
  21. plt.plot(x0, y1, 'r--', label='poly_fit values')
  22. plt.xlabel('x axis')
  23. plt.ylabel('y axis')
  24. plt.legend(loc="lower right")
  25. plt.title('Poly Fitting (y={:.3f}x+{:.3f})'.format(a1, a0))#格式化输出
  27. >>> p1(1997)
  28. 233.42857142858702
  29. >>> p1(1998)
  30. 253.92857142858702
  32. >>> fun(1997,a0,a1)
  33. 233.42857142858702
  34. >>> fun(1998,a0,a1)
  35. 253.92857142858702

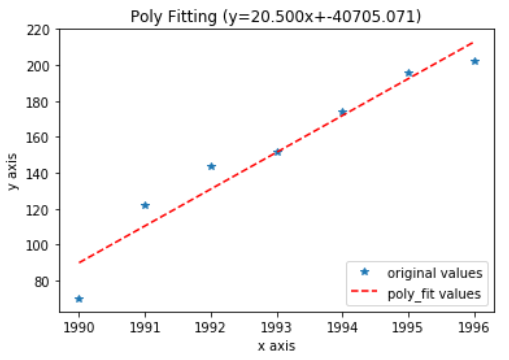
image.png

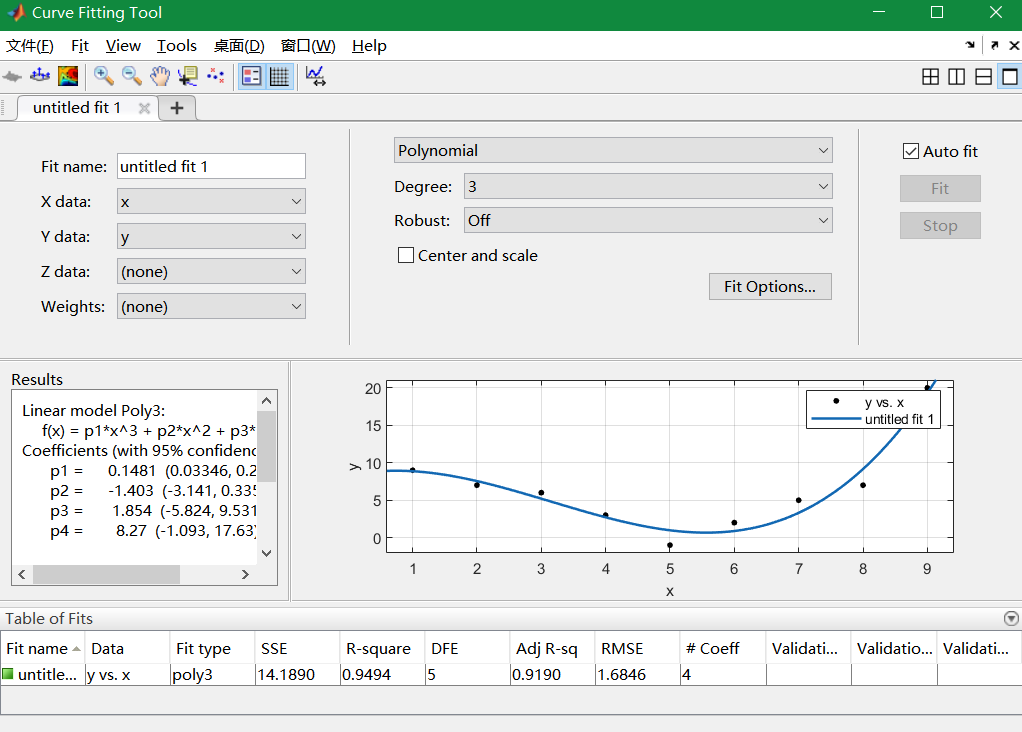
matlab图形窗口的多项式拟合

plot(x,y,’r*’)—>工具—>基本拟合
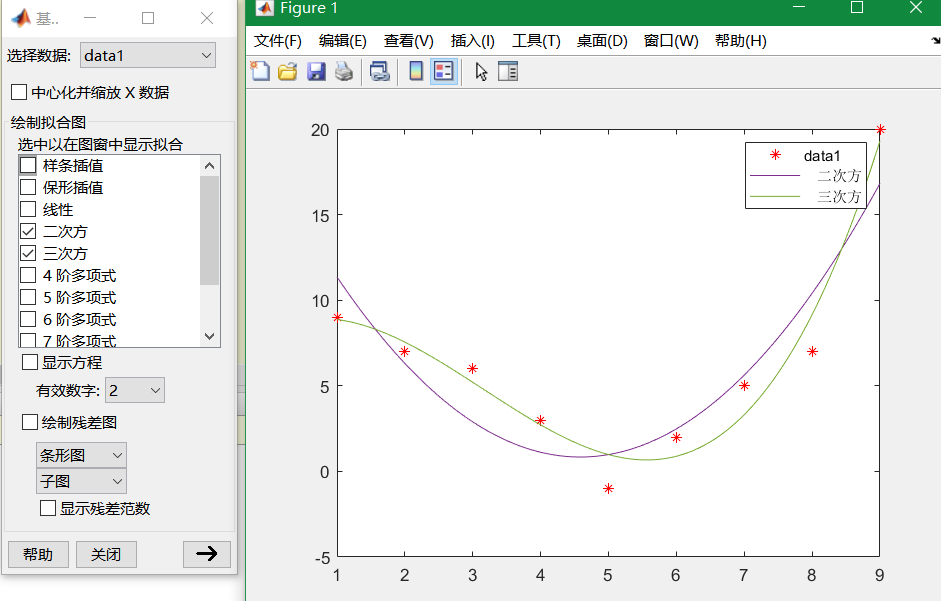
image.png

matlab强大的拟合工具箱Curve Fitting

曲线拟合的最小二乘法 - 图5

函数逼近

  • 用一个简单的函数逼近较为复杂的连续函数
  • 选择一组基曲线拟合的最小二乘法 - 图6构造曲线拟合的最小二乘法 - 图7来逼近曲线拟合的最小二乘法 - 图8，使得曲线拟合的最小二乘法 - 图9最小，利用极值的充分必要条件得下列等式

曲线拟合的最小二乘法 - 图10

例2

  • 求曲线拟合的最小二乘法 - 图11在曲线拟合的最小二乘法 - 图12中的最佳平方逼近多项式。

    matlab求解

    1. syms x
    2. base=[1,x^2,x^4];
    3. y1=base.'*base 
    4. % a'对a的每个元素取共轭，然后再转置;  a.'只对a转置
    5. y2=cos(x)*base.'
    6. r1=int(y1,-pi/2,pi/2)%int积分
    7. r2=int(y2,-pi/2,pi/2)
    8. a=r1\r2%/（向右倒称为右除） 右除    AB=C    A=C/B
    9.      %\（向左倒称为左除） 左除    AB=C    B=A\C
    10. xishu1=double(a)
    11. xishu2=vpa(a,6) %设置精度