• 数模比赛中，常常需要根据已知的函数点进行数据、模型的处理和分析，而有时候现有的数据是极少的，不足以支撑分析的进行，这时就需要使用一些数学的方法，“模拟产生”一些新的单又比较靠谱的值来满足需求，这就是插值的作用。

  • 插值法在数值分析课程中有详细介绍。

    一维插值函数

  • y = interp1(x0, y0, x, ‘menthod’)

  • method 指定插值的方法，默认为线性插值。其值可为： | ‘nearest’ | 最近项插值 | | —- | —- | | ‘linear’ | 线性插值 | | ‘spline’ | 立方样条插值 | | ‘cubic’ | 立方插值 |

  • 当 x0 为等距时可以用快速插值法，使用快速插值法的格式为‘nearest’, ‘linear’, ‘spline’, ‘cubic’

    三次样条插值

  1. y = interp1(x0, y0, x, ‘spline’)
  2. y = spline(x0, y0, x)
  3. pp = csape(x0, y0, conds)
  4. pp = csape(x0, y0, conds, valconds); y = fnal(pp, x)
  • 对于三次样条插值，提倡使用函数 csape 。

  • condas: csape默认边界条件为Lagrange边界条件，其值可为： | ‘complete’ | 一阶导数 | | —- | —- | | ‘not-a-knot’ | 非扭结条件（没有边界条件） | | ‘periodic’ | 周期条件 | | ‘second‘ | 二阶导数 |

  • valconds默认导数值 [ 0, 0 ]

    例1

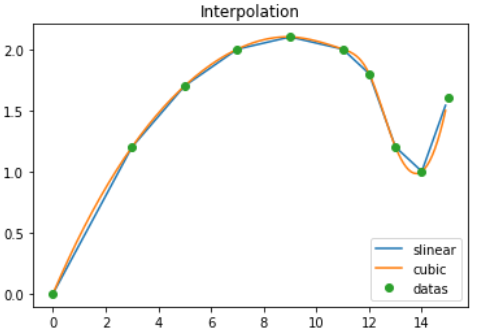
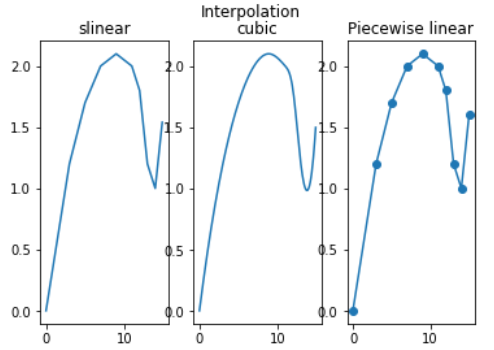
  • 给出下表数据，需要得到 x 坐标每改变0.1时的y坐标，并画出曲线。用分段线性和三次样条插值方法计算。 | x | 0 | 3 | 5 | 7 | 9 | 11 | 12 | 13 | 14 | 15 | | —- | —- | —- | —- | —- | —- | —- | —- | —- | —- | —- | | y | 0 | 1.2 | 1.7 | 2.0 | 2.1 | 2.0 | 1.8 | 1.2 | 1.0 | 1.6 |

matlab求插值

  1. x0=[0   3   5   7   9   11   12   13   14  15];
  2. y0=[0  1.2  1.7  2.0  2.1  2.0  1.8  1.2   1.0  1.6];
  3. x = 0:0.1:15;
  4. y1 = interp1(x0,y0,x);%默认线性插值
  5. y2 = interp1(x0,y0,x,'spline');%三次样条插值
  6. pp1=csape(x0,y0);%边界条件为Lagrange条件
  7. y3=fnval(pp1,x);
  9. subplot(1,3,1)
  10. plot(x0,y0,'+',x,y1)
  11. title('Piecewise linear')
  13. subplot(1,3,2)
  14. plot(x0,y0,'+',x,y2)
  15. title('Spline1')
  17. subplot(1,3,3)
  18. plot(x0,y0,'+',x,y3)
  19. title('Spline2')

image.png

python求插值

  1. import numpy as np
  2. from scipy import interpolate #插值
  3. import matplotlib.pyplot as plt #Pyplot 是 Matplotlib 的子库，提供了和 MATLAB 类似的绘图 API。Pyplot 是常用的绘图模块，能很方便让用户绘制 2D 图表。
  4. x0 = np.array([0, 3, 5, 7, 9, 11, 12, 13, 14, 15])
  5. y0 = np.array([0, 1.2, 1.7, 2.0, 2.1, 2.0, 1.8, 1.2, 1.0, 1.6])
  6. x1 = np.arange(0, 15, 0.1)#numpy.arange(start, stop, step, dtype)  np.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)
  7. plt.figure(figsize=(8, 6))#创建一个8*6点（point）的点图
  9. ###将图作在一张图上
  10. for method in [ "slinear", "cubic"]:  # 插值方式
  11.     f = interpolate.interp1d(x0, y0, kind=method) #一维数据的插值运算可以通过方法 interp1d() 完成。kind=method指插值方法
  12.     y1 = f(x1)#得到插值结果
  13.     plt.plot(x1, y1, label=method)
  14. plt.plot(x0,y0,'o',label="datas")
  15. plt.title('Interpolation')
  16. plt.legend(loc="lower right")#图例的位置
  17. plt.show()
  19. ###3张子图
  20. i=1
  21. for method in [ "slinear", "cubic"]:  # 插值方式
  22.     f = interpolate.interp1d(x0, y0, kind=method) #一维数据的插值运算可以通过方法 interp1d() 完成。kind=method指插值方法
  23.     y1 = f(x1)#得到插值结果
  24.     plt.subplot(1, 3, i)
  25.     plt.plot(x1, y1)
  26.     plt.title(method)
  27.     i=i+1
  28. plt.subplot(1, 3, i)
  29. plt.plot(x0,y0,'o-')
  30. plt.title("Piecewise linear")
  31. plt.suptitle('Interpolation')
  32. plt.show()

image.png image.png

二维插值

插值节点为网格节点

  • 已知插值方法 - 图4。求点插值方法 - 图5
  • z = interp2( x0, y0, z0, x, y, ‘ method ‘) 注意：x0, y0分别是m维和n维向量，z0是n×m矩阵。x是M维行向量，y是N维列向量，z是N×M矩阵

  • 三次样条插值 pp = csape( {x0, y0}, z0, conds, valconds), z=fnval(pp, {x, y}) 注意：x0, y0分别是m维和n维向量，z0是m×n矩阵。x是M维向量，y是N维向量，z是M×N矩阵

    例2

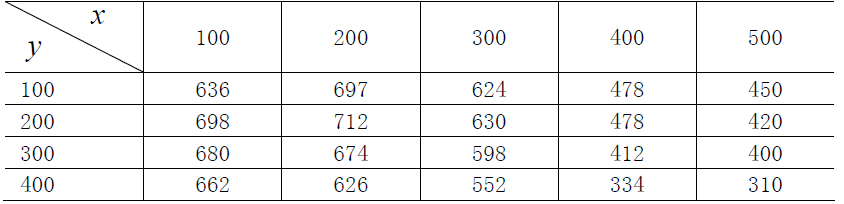
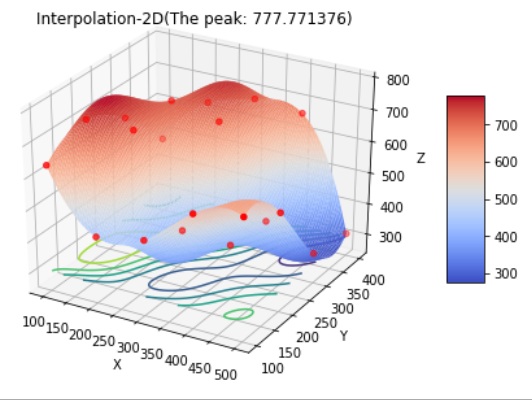
  • 在一丘陵地带测量高程，插值方法 - 图6和插值方法 - 图7方向每隔100m 测一个点，得到高程表如下，试插值一个曲面，确定合适的模型，并由此找到最高点和该点的高程。

image.png

matlab求解

  1. clear,clc
  2. x=100:100:500;
  3. y=100:100:400;
  4. z=[636    697    624    478   450  
  5.    698    712    630    478   420
  6.    680    674    598    412   400
  7.    662    626    552    334   310];
  9. xi=100:10:500;yi=100:10:400;
  10. pp=csape({x,y},z');
  11. cz=fnval(pp,{xi,yi});
  12. [i,j]=find(cz==max(max(cz)));
  13. disp(["最高点的地址：" num2str([xi(i),yi(j)])]);
  14. disp(["最高点的高程：" num2str(cz(i,j))]);
  15. [X,Y]=meshgrid(xi,yi);
  16. surf(X,Y,cz')
  1. "最高点的地址："    "170  180"<br />    "最高点的高程："    "720.6252"<br />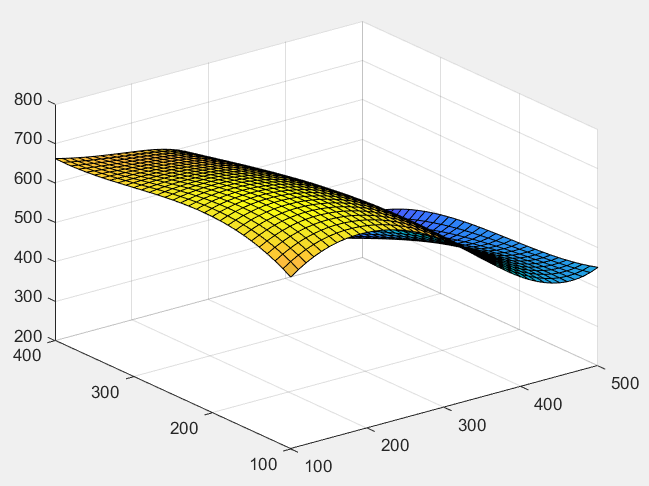![image.png](https://cdn.nlark.com/yuque/0/2022/png/27273066/1650804028912-6aeb3f2d-4863-4833-9879-7ec2011e8095.png#clientId=uabc0933f-017c-4&crop=0&crop=0&crop=1&crop=1&from=paste&height=374&id=u06c367dc&margin=%5Bobject%20Object%5D&name=image.png&originHeight=486&originWidth=649&originalType=binary&ratio=1&rotation=0&showTitle=false&size=57793&status=done&style=none&taskId=ud3cda361-1d5f-4b79-aaa7-58792bd71a3&title=&width=499.2307875424454)

python求解

  1. import numpy as np
  2. from scipy import interpolate #插值
  3. import matplotlib.cm as cm #曲面的配色
  4. import matplotlib.pyplot as plt #绘图
  5. from mpl_toolkits.mplot3d import Axes3D #3D图
  7. x0, y0 = np.mgrid[100:500:5j, 100:400:4j]#生成网格图5*4,5j代表5段，没有j代表间距为5
  8. z0 = np.array([636, 697, 624, 478, 450,
  9.                698, 712, 630, 478, 420,
  10.                680, 674, 598, 412, 400,
  11.                662, 626, 552, 334, 310]).reshape((4, 5))
  12. z0=z0.T#注意z是5*4
  14. f = interpolate.interp2d(x0, y0, z0, kind='cubic')#由样本点生成三次样条插值
  15. x1 = np.linspace(100, 500, 100)#np.linspace(start, stop, num=50)
  16. y1 = np.linspace(100, 400, 100)
  17. z1 = f(x1, y1)#插值结果
  19. x1, y1 = np.meshgrid(x1, y1)
  20. fig = plt.figure()
  21. ax=Axes3D(fig)#3D对象
  22. #ax=fig.add_subplot(111,projection='3d')
  23. #ax= plt.subplot(1, 2, 1, projection='3d')
  24. surf = ax.plot_surface(x1, y1, z1, rstride=1, cstride=1,
  25.                          cmap=cm.coolwarm, linewidth=0.5, antialiased=True)#rstride行之间的跨度，cstride列之间的跨度cmap颜色映射表，默认是“rainbow”
  26. plt.title('Interpolation-2D(The peak: {:3f})'.format(np.max(z1)))
  27. ax.scatter(x0,y0,z0,c='r')#三维散点图
  28. ax.contour(x1, y1, z1,zdir='z',offset=300)#投影到z平面的z=300上
  29. ax.set_zlabel('Z')  # 坐标轴
  30. ax.set_ylabel('Y')
  31. ax.set_xlabel('X')
  32. plt.colorbar(surf, shrink=0.5, aspect=5)
  33. plt.show()
  35. #最高点处的地址
  36. x1[np.where(z1==np.max(z1))] #array([144.44444444])
  37. y1[np.where(z1==np.max(z1))] #array([200.])

image.png

插值节点为散乱节点

  • 已知插值方法 - 图10个节点，插值方法 - 图11，求点插值方法 - 图12处的插值插值方法 - 图13。

  • ZI = griddata(x, y, z, XI, YI ) 注意：x y z 均为n维向量，指明所给数据点的横坐标、纵坐标和竖坐标；向量XI YI是给定的网格点的横坐标和纵坐标，一个是行向量，另一个是列向量；返回值ZI 为网格（XI,YI）处的函数值。

    例3

  • 下表是海底水深数据，在适当矩形区域内画出海底曲面的图形。

image.png

matlab求解

  1. clc, clear
  2. clc, clear
  3. x=[129,140,103.5,88,185.5,195,105,157.5,107.5,77,81,162,162,117.5];
  4. y=[7.5,141.5,23,147,22.5,137.5,85.5,-6.5,-81,3,56.5,-66.5,84,-33.5];
  5. z=-[4,8,6,8,6,8,8,9,9,8,8,9,4,9];
  6. xmm=minmax(x);  %求x的最小值和最大值
  7. ymm=minmax(y);  %求y的最小值和最大值
  8. xi=xmm(1):xmm(2);
  9. yi=ymm(1):ymm(2);
  10. zi1=griddata(x,y,z,xi,yi','cubic'); %立方插值
  11. zi2=griddata(x,y,z,xi,yi','nearest'); %最近点插值
  12. zi=zi1;  %立方插值和最近点插值的混合插值的初始值
  13. zi(isnan(zi1))=zi2(isnan(zi1));  %把立方插值中的不确定值换成最近点插值的结果
  14. subplot(1,2,1), plot(x,y,'*');
  15. subplot(1,2,2), mesh(xi,yi,zi);