Malthus模型

模型假设：

1. 表示时刻的人口数，且连续可微。
2. 人口的增长率是常数（增长率=出生率-死亡率）。
3. 人口数量的变化是封闭的，即人口数量的增加与减少只取决于人口中个体的生育和死亡，且每一个个体都具有同样的生育能力和死亡率。

   建模与求解

   时刻到时刻人口的增量为
   
   于是得
   
   其解为
   

   模型评价

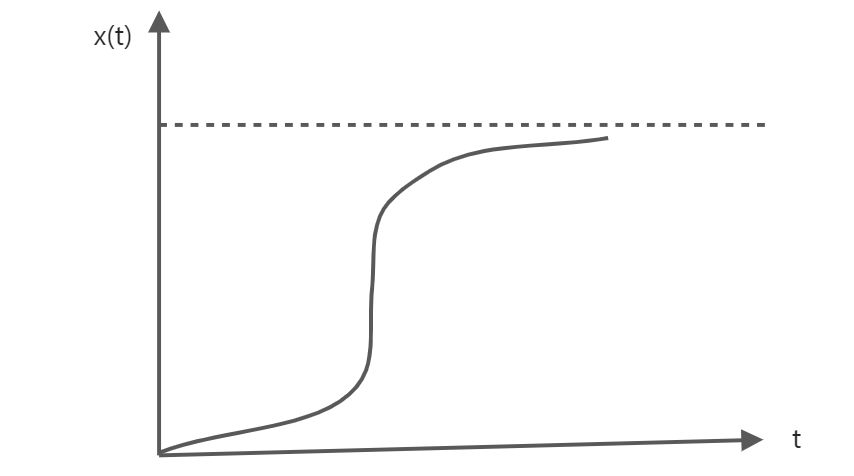
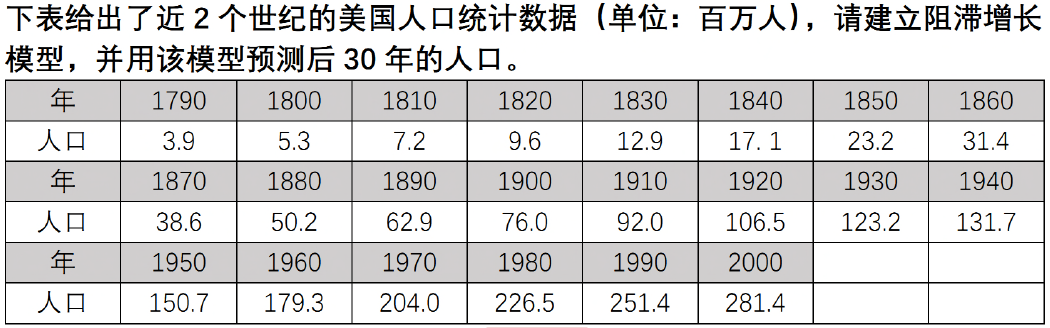
   该模型在预测1700-1961年间世界人口增长与实际情况较为符合，但是当 t 很大时，人口数量就大的惊人，这是因为增长率为常数，所以人口数一直在增加，但实际是增长率是变动的。

   阻滞增长模型（Logistic模型）

• 我们这里要对增长率进行修正。地球上得资源是有限的，随着人口数量的增加，资源对人口增长的限制作用越来越显著，即将增长率 表示为人口 的减函数 。

  模型假设

1. 设为的线性函数，（工程师原则，首先用线性）。

2. 自然资源与环境条件所能容纳的最大人口数为，即当时，增长率。

   建模与求解

   由假设可得，则有
   
   其解为
   

   模型检验

   
   人口总数有以下规律：

3. ，即无论人口初值如何，人口总数都以为极限。

4. 当时，单调增加，且时，为凹函数，时，为凸函数。
5. 人口变化率在时取到最大值。

美国人口的预报模型

建模与求解

我们取初值
，则，其中和是待估拟合参数。

非线性最小二乘拟合

使用阻滞增长模型预测美国人口.pdf