区间估计
例1
- 分别使用金球和铂球测定引力常数(单位:
)。
(1)用金球测定观察值为6.683,6.681,6.676,6.678,6.679,6.672。
(2)用铂球测定观察值为6.661,6.661,6.667,6.667,6.664。
设测定值总体为均为未知,试就(1),(2)两种情况分别求
的置信度为0.9的置信区间,并求
的置信度为0.9的置信区间。
(3)设用金球和铂球测定时总体的方差相等,求两个测定值总体均值差的置信度为0.90的置信区间。
解:
(1)均未知时,
的置信度为0.9的置信区间为
(2)均未知时,
的置信度为0.9的置信区间为
(3)总体均值差的置信度为0.90的置信区间为
clc,clearx1=[6.683,6.681,6.676,6.678,6.679,6.672];x2=[6.661,6.661,6.667,6.667,6.664];%如果检验在 5%(默认) 的显著性水平上拒绝原假设,则结果 h 为 1,否则为 0。%p假设检验的p值。%均值的置信区间 ci,以及包含检验统计量信息的结构体 stats。[h1,p1,ci1,st1]=ttest(x1,mean(x1),'Alpha',0.1)%t检验可求得均值的置信区间[h2,p2,ci2,st2]=ttest(x2,mean(x2),'Alpha',0.1)[h3,p3,ci3,st3]=vartest(x1,var(x1),'Alpha',0.1)[h4,p4,ci4,st4]=vartest(x2,var(x2),'Alpha',0.1)[h,p,ci,st]=ttest2(x1,x2,'Alpha',0.1)%双样本t检验
# 方差既可以使用numpy函数,也可以使用pandas函数。## numpy 中计算的方差就是样本方差本身:## 使用场景为:拥有所有数据的情况下,计算所有数据的标准差时使用,即最终除以n,而非n-1### pandas 中计算的方差为无偏样本方差:## 使用场景为:只有部分数据但需要求得总体的标准差时使用,当只有部分数据时,根据统计规律,除以n时计算的标准差往往偏小,因此需要除以n-1,即n-ddof。## 由于是用于样本数据,所以采用pandas的方差函数。import pandas as pdimport numpy as npfrom scipy import statsx1 = pd.Series([6.683,6.681,6.676,6.678,6.679,6.672])x2 = pd.Series([6.661,6.661,6.667,6.667,6.664])x1_mean,x1_var,x1_std=stats.bayes_mvs(x1,alpha=0.90)x2_mean,x2_var,x2_std=stats.bayes_mvs(x2,alpha=0.90)print('总体x1均值的置信度为0.90的置信区间是{}'.format(x1_mean))print('总体x1方差的置信度为0.90的置信区间是{}'.format(x1_var))print('总体x2均值的置信度为0.90的置信区间是{}'.format(x2_mean))print('总体x2方差的置信度为0.90的置信区间是{}'.format(x2_var))
注:python区间估计和假设检验部分可查看我的这份笔记。
语雀:https://www.yuque.com/chenyujiao-4zrlp/sxmd8u/adwx4l
jupter notebook:http://localhost:8888/notebooks/Documents/python%E6%95%B0%E6%8D%AE%E5%88%86%E6%9E%90/%E7%AC%AC6%E7%AB%A0%20%E7%AE%80%E5%8D%95%E7%BB%9F%E8%AE%A1%E6%8E%A8%E6%96%AD.ipynb
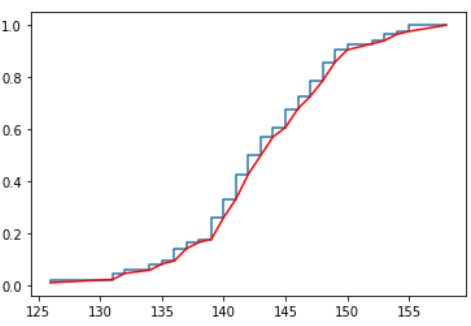
经验分布函数
设是总体
的一个容量为
的样本值。从小到大排序后:
对于经验分布函数,格里汶科(Glivenko)证明了当时,
以概率1一致收敛于总体分布函数
。
例2
下面给出了84个伊特拉斯坎任男子的头颅的最大宽度(mm),计算经验分布函数并画出经验分布函数图形。
141 148 132 138 154 142 150 146 155 158 150 140 147 148 144 150 149 145 149 158 143 141 144 144 126 140 144 142 141 140 145 135 147 146 141 136 140 146 142 137 148 154 137 139 143 140 131 143 141 149 148 135 148 152 143 144 141 143 147 146 150 132 142 142 143 153 149 146 149 138 142 149 142 137 134 144 146 147 140 142 140 137 152 145
clc,clearload 'data.mat' #数据在一维数组data中[ycdf,xcdf,n]=cdfcalc(data);%注意得出的经验分布的值没有保留重复值cdfplot(data)title("")hold onplot(xcdf,ycdf(2:end),'r*')
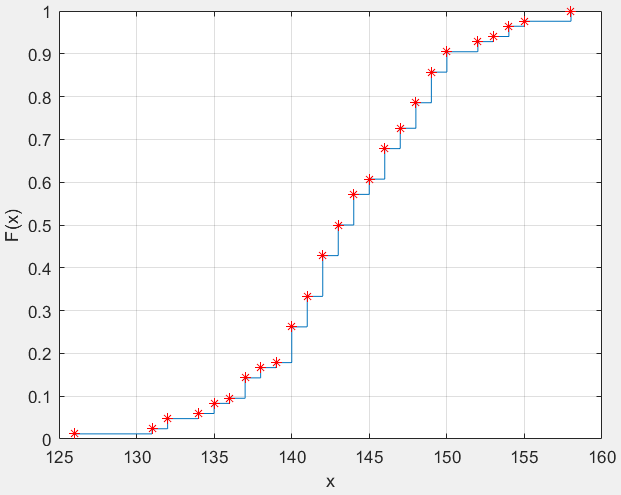
"""经验分布函数"""import numpy as npfrom statsmodels.distributions.empirical_distribution import ECDFimport pandas as pddata=pd.read_excel(r'ex7_5.xls')ecdf=ECDF(data['data'])sort_data=data.sort_values(by='data')['data']ecdf(sort_data)import matplotlib.pyplot as pltplt.figure()plt.step(sort_data,ecdf(sort_data))plt.plot(sort_data,ecdf(sort_data),'r-')
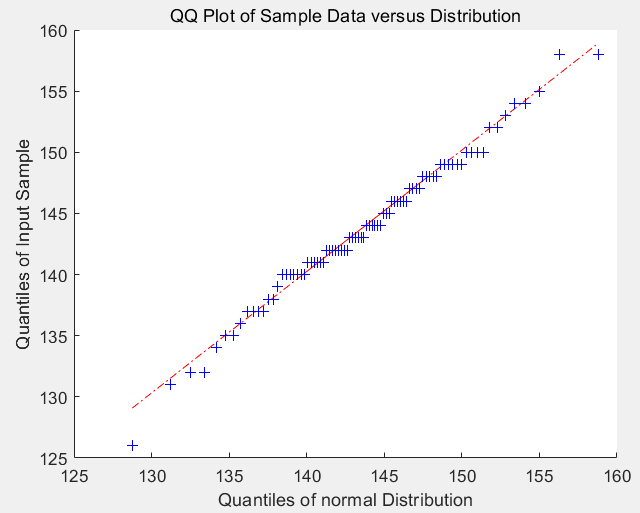
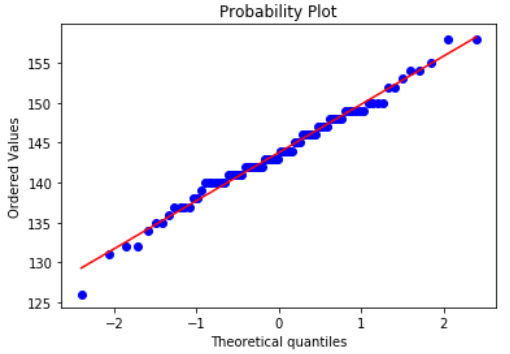
Q-Q图
作用
Q-Q图(Quantile-Quantile Plot)是检验拟合优度的好办法。对于一组观察数据
,利用参数估计方法确定了分布模型的参数
后,分布函数
就知道了,现在希望知道的是观测数据与分布模型的拟合效果如何。
原理
Q-Q图的基本思想是将经验分布函数的分位数点和分布模型的理论分布分位数点作为一堆数组画在直角坐标图上,就是一个点,
个观测数据对应
个点,如果这
个点看起来像一条直线,说明观测数据与分布模型的拟合效果很好。
计算步骤
- 如果这些数据来自于正态总体,求该正态分布的参数,试画出它们的Q-Q图,判断拟合效果。
clc,clearload 'data.mat'mean_data=mean(data);std_data=std(data);%PD = ProbDistUnivParam(DistName, Params) 创建 PD,这是一个 ProbDistUnivParam 对象,它表示概率分布。此分布由 DistName 指定的参数分布定义,参数由数值矢量参数指定。pd=makedist('normal','mu',mean_data,'sigma',std_data);%qqplot(X) %检查数据X是否副总正态分布,这和正态概率函数差不多%qqplot(X,Y) %检验数据X与Y是否服从相同的分布(他们的每个分位数是否都相近相似)qqplot(data,pd)
from scipy import statsdata.mean()data.std()stats.probplot(sort_data, dist="norm",plot=plt)plt.show()
非参数检验
拟合优度检验
步骤
- 建立待检验假设
:总体
的分布函数为
。
- 若总体
是离散型的,建立待检假设
:总体
的分布律为
。
- 若总体
是连续型的,建立待检假设
:总体
的概率密度为
。
- 若总体
- 将数轴分成
个区间,令
为分布函数
的总体
在第
个区间内取值的概率,设
为
个样本观察值落入第
个区间上的个数,也称为组频数。
- 选取统计量
,如果
为真,则
,其中
为分布函数
中未知参数的个数,
为分组的组数。
- 给定显著性水平
,确定
并计算样本统计量
的观察值。
- 作出判断:若
,则接受
;否则拒绝
,即不能认为总体
的分布函数为
。
续例2
- 试检验这些数据是否来自正态总体(取
)。
解::头颅的最大宽度
服从正态分布
。
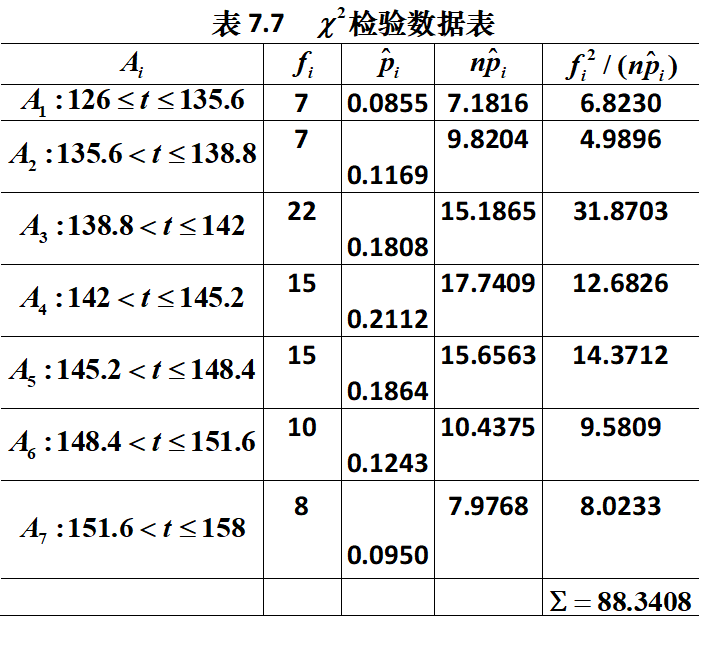
所以接受假设,认为这些数据是来自正态总体。
clc,clearload 'data.mat'%创建正态分布的方法一:这种方法两个参数是待估的pd_f=fitdist(data','Normal')%对数据进行概率分布对象拟合,用数据拟合正态分布得到的参数的点估计和区间估计%创建正态分布的方法二:mean_data=mean(data);std_data=std(data);pd_m=makedist('normal','mu',mean_data,'sigma',std_data);%创建概率分布对象,有和fitdist一样的方法%得到分布函数的方法一:这种方法两个参数是确定的pd_cdf=@(x) cdf(pd_f,x)或pd_cdf=@(x) cdf(pd_m,x)%得到分布函数的方法二:pd_cdf=@(x) normcdf(x,mean_data,std_data)%qqplot(X) %检查数据X是否服从正态分布,这和正态概率函数差不多%qqplot(X,Y) %检验数据X与Y是否服从相同的分布(他们的每个分位数是否都相近相似)qqplot(data,pd)%默认bins为10,会使得观测数均在5个以上。%‘emin’非负整数,默认值5,指定一个区间对应的最小理论频数%‘frequency’与x等长的向量, 指定x中各元素出现的频数%‘alpha’默认值0.05 ,指定检验的显著性水平[h,p,st]=chi2gof(data,'cdf',pd_cdf,'NParams',2,'Alpha',0.1) %cdf指分布函数;‘expected’指定各区间的理论频数,与‘cdf’不能同时出现[h,p,st]=chi2gof(data,'cdf',pd_f,'Alpha',0.1) %由fitdist得到的分布对象,r=2,统计量的自由度为k-r-1=4[h,p,st]=chi2gof(data,'cdf',pd_m,'Alpha',0.1) %由makedist得到的分布对象,r=0,统计量的自由度为k-r-1=6%本题中,两个参数是估计出来的,所以选第一种或第二种,r=2才对
结果:
h =0p =0.3618st =包含以下字段的 struct:chi2stat: 4.3408 %样本统计量的结果df: 4 %自由度edges: [126.0000 135.6000 138.8000 142.0000 145.2000 148.4000 151.6000 158.0000] %分组的边界值O: [7 7 22 15 15 10 8]%实际频数E: [7.1816 9.8204 15.1865 17.7409 15.6563 10.4375 7.9768]%理论频数>>> chi2inv(0.9,st.df)%临界值ans =7.7794
例3
- 在一批灯泡中抽取300只作寿命试验,取
,试检验假设:
:灯泡寿命服从指数分布。
| 寿命 |
||||
|---|---|---|---|---|
| 灯泡数 | 121 | 78 | 43 | 58 |
解:
clc,clearedges=[0:100:300 inf];bins=[50 150 250 inf];num=[121 78 43 58];pd=makedist('exp',200);pd_cdf=@(x) cdf(pd,x);[h,p,st]=chi2gof(bins,'Edges',edges,'cdf',pd_cdf,'Frequency',num,'NParams',0)chi2=chi2inv(0.95,st.df)结果:h = 0p = 0.6052st =包含以下字段的 struct:chi2stat: 1.8450df: 3edges: [0 100 200 300 Inf]O: [121 78 43 58]E: [118.0408 71.5954 43.4248 66.9390]chi2= 7.8147
从h=0和chi2stat<chi2和p>0.05都可以说明接受原假设,即认为这批灯泡寿命服从参数为200的指数分布。
柯尔莫哥洛夫检验
原理
拟合优度检验实际上是检验
的正确性,并未直接检验原假设的分布函数
的正确性,柯尔莫哥洛夫检验直接针对原假设
,这里分布函数
必须是连续型分布。柯尔莫哥洛夫检验基于经验分布函数作为检验统计量,检验理论分布函数与样本分布函数的拟合优度。
- 设总体
服从连续分布,
是来自总体
的简单随机样本,
为经验分布函数。定义
步骤
- 原假设和备择假设
- 选取检验统计量
当为真时,
有偏小趋势,则拟合得越好。
- 确定拒绝域。给定显著性水平
,查
极限分布表,求出
满足
即拒绝域为。
| 0.1 | 0.05 | 0.01 | |
|---|---|---|---|
| 1.22 | 1.36 | 1.63 |
- 试用柯尔莫哥洛夫检验法检验这些数据是否服从正态分布(
)。
解:
- 拒绝域是
- 计算经验分布函数
和理论分布函数值
,并计算统计量
所以接受原假设,即认为服从正态分布。
clc,clearload 'data.mat'%% 方法一:由该方法的步骤计算mean_data=mean(data);std_data=std(data);[ycdf,xcdf,n]=cdfcalc(data);%经验分布ycdf=ycdf(1:end-1);%% 这里有一点疑惑,按照经验分布函数的定义,不应该是去掉第一个数据0吗pd_cdf=@(x) normcdf(x,mean_data,std_data);%理论分布%pd_cdf=normcdf(xcdf,mean_data,std_data);Dn=max(abs(ycdf - pd_cdf(xcdf)));if Dn*sqrt(length(data))<1.36disp("接受原假设")elsedisp("拒绝原假设")end%% 方法二:调用工具箱pd=makedist('Normal','mu',mean_data,'sigma',std_data);[h,p,st,cv]=kstest(data,'CDF',pd,'Alpha',0.05)%cv是临界值,和上面结果不一样是因为这里的t更准确
结果:
h = 0 %代表接受原假设p = 0.5484 %p值大于显著性水平0.05,所以接受原假设st = 0.0851 %代入样本数据得到的统计量的值,大于临界值cv,所以接受原假设cv = 0.1461 %临界值
秩和检验
作用
- 将两个样本混合起来,按照数值从小到大统一排序,每个数据对应的序数为秩。
- 计算取自总体
的样本所对应的秩之和,用
表示。
- 根据
与水平
,查秩和检验表,得秩和下限
和秩和上限
。
- 若
,则否定原假设,认为两个总体分布有显著差异。
原理
如果两总体分布无显著差异,那么不应太大或太小。
例3
- 试讨论烘干温度对抗弯强度在水平
下是否有显著影响?
解:
- 排序
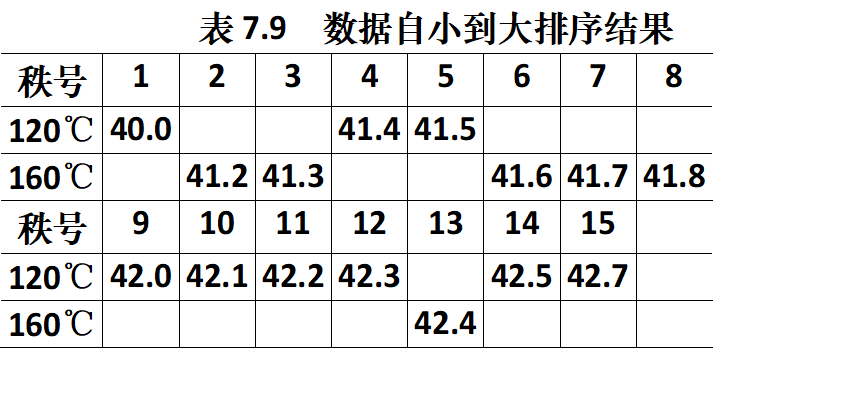
- 查表
,接受原假设,认为没有显著差异 ```matlab clc, clear x=[41.5 42.0 40.0 42.5 42.0 42.2 42.7 42.1 41.4]; y=[41.2 41.8 42.4 41.6 41.7 41.3]; yx=[y,x]; yxr=tiedrank(yx);%计算秩 yr=sum(yxr(1:length(y)));%计算y的秩和
%% 利用工具箱 [p,h,st]=ranksum(y,x,’Alpha’,0.05) ```