• 回归中关于自变量的选择大有门道，变量过多可能会导致多重共线性问题造成回归系数的不显著，甚至造成OLS估计的失效。

• 岭回归和lasso回归在OLS回归模型的损失函数(残差平方和SSE)上加上了不同的惩罚项，该惩罚项由回归系数的函数构成，一方面，加入的惩罚项能够识别出模型中不重要的变量，对模型起到简化作用，可以看作逐步回归的升级班；另一方面，加入的惩罚项会让模型变得可估计，即使之前的数据不满足列满秩。

  岭回归的原理

• 多元线性回归：，其中

• 岭回归：为一正常数。

记，时，岭回归和多元线性回归完全相同；时，
另外：
由于半正定，则特征值均为非负数，加上后，特征值均为整数，则可逆，所以

如何选择

岭迹分析(用得比较少)

• 岭迹的概念：将从变量，得到的中每个变量的变化曲线。
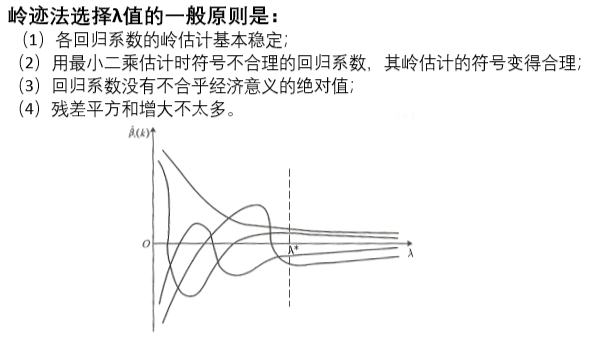
• 用岭迹法选择的一般原则是：
  （1）各回归系数的岭估计基本稳定；
  （2）用最小二乘估计时符号不合理的回归系数，其岭估计的符号变得合理；
  （3）回归系数没有不合乎经济意义的绝对值；
  （4）残差平方和增大不太多。

VIF法（方差膨胀因子）（几乎不用）

• 不断增加，直到所有的的

  最小化均方预测误差（用的最多）

• 我们使⽤ K 折交叉验证的⽅法来选择最佳的调整参数。所谓的K 折交叉验证，是说将样本数据随机分为 K 个等分。将第 1 个⼦样本作为 “验证集”（validation set）⽽保留不⽤，⽽使⽤其余 K-1 个⼦样本作为 “训练集”（training set）来估计此模型，再以此预测第 1 个⼦样本，并计算第1个⼦样本的 “均⽅预测误差”（Mean Squared Prediction Error）。其次，将第 2 个⼦样本作为验证集，⽽使⽤其余 K-1 个⼦样本作为训练集来预测第2个⼦样本，并计算第 2 个⼦样本的 MSPE。以此类推，将所有⼦样本的 MSPE 加总，即可得整个样本的 MSPE。最后，选择调整参数 ，使得整个样本的 MSPE 最⼩，故具有最佳的预测能⼒。

• 注意：我们需要保证量纲一致，若不同可考虑标准化

  Lasso回归的原理

• 多元线性回归：，其中

• 岭回归：为一正常数。
• Lasso回归（用得多）：

Lasso回归与岭回归模型相比，其最大的优点是可以将不重要的变量的回归系数压缩至0，而岭回归虽然也对原来系数做了一定程度的压缩，但是任一系数都不会为，最终的模型保留了搜索变量。可以用上述的“最小化均方预测误差”来确定。

何时使用Lasso回归

1. 首先使用最一般的OLS对数据进行回归，然后计算方差膨胀因子VIF，如果VIF>10则说明存在多重共线性的问题，因此需要对变量进行筛选。
2. 使用lasso回归筛选出不重要的变量（lasso回归可以看陈逐步回归的进阶版）
   1. 判断自变量的量纲是否一样，如果不一样则首先进行标准化的预处理
   2. 对变量进行lasso回归，记录下lasso回归结果表中回归系数不为0的变量，这些变量就是最终我们要留下来的重要变量
3. 将这些重要变量视为自变量，进行回归，并分析结果。（此时的变量可以是标准化前的，lasso回归只起到变量筛选的目的）