检索结果的排序是否合理,往往决定了一个检索系统的质量,在搜索引擎这样的大规模检索系统中,排序是非常核心的一个环节。简单来说,排序就是搜索引擎对符合用户要求的检索结果进行打分,选出得分最高的 K 个检索结果的过程。这个过程也叫作 Top K 检索。
经典的 TF-IDF 算法
计算相关性,就必须要提到经典的 TF-IDF 算法了,它能很好地表示一个词在一个文档中的权重。TF-IDF 算法的公式是:相关性 = TF * IDF。其中,TF 是词频(Term Frequency),IDF 是逆文档频率(Inverse Document Frequency)。
文档频率(Document Frequency),指的是这个词项出现在了多少个文档中。你也可以理解为,如果一个词出现在越多的文档中,那这个词就越普遍,越没有区分度。一个极端的例子,比如“的”字,它基本上在每个文档中都会出现,所以它的区分度就非常低。
那为了方便理解和计算相关性,我们又引入了一个逆文档频率的概念。逆文档频率是对文档频率取倒数,它的值越大,这个词的的区分度就越大。
因此, TFIDF 表示了我们综合考虑了一个词项的重要性和区分度,结合这两个维度,我们就计算出了一个词项和文档的相关性。不过,在计算的过程中,我们会对 TF 和 IDF 的值都使用对数函数进行平滑处理。处理过程如下图所示: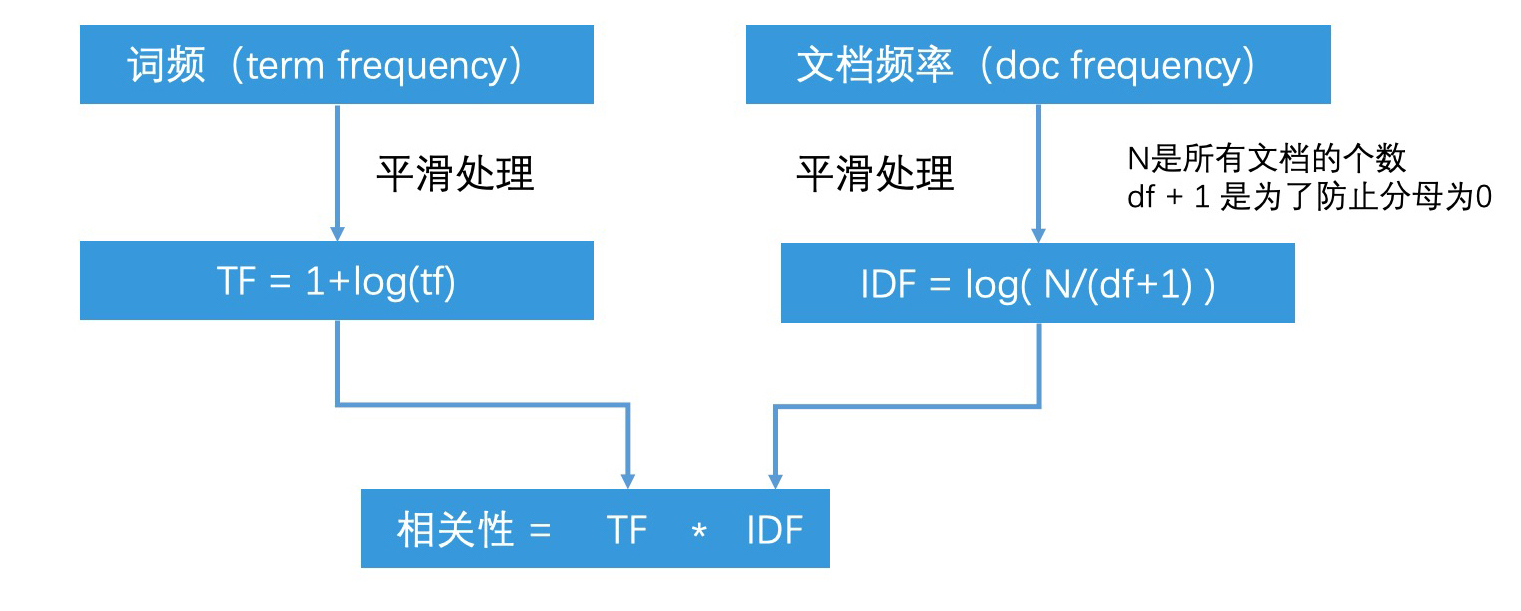
但是,很多情况下,一个查询中会有多个词项。不过,这也不用担心,处理起来也很简单。我们直接把每个词项和文档的相关性累加起来,就能计算出查询词和文档的总相关性了。例子如此下:
假设查询词是“极客时间”,它被分成了两个词项“极客”和“时间”。现在有两个文档都包含了“极客”和“时间”,在文档 1 中,“极客”出现了 10 次,“时间”出现了 10 次。而在文档 2 中,“极客”出现了 1 次,“时间”出现了 100 次。
那两个文档的最终相关性得分如下:
文档 1 打分 =TFIDF(极客)+ TFIDF(时间)= (1+log(10)) 2 + (1+log(10)) 1 = 4 + 2 = 6
文档 2 打分 = TFIDF(极客)+ TFIDF(时间)=(1+log(1)) 2 + (1+log(100)) * 1 = 2 + 3 = 5
你会发现,尽管“时间”这个词项在文档 2 中出现了非常多次,但是,由于“时间”这个词项的 IDF 值比较低,因此,文档 2 的打分并没有文档 1 高。
概率模型中的 BM25 算法
在实际使用中,我们往往不会直接使用 TF-IDF 来计算相关性,而是会以 TF-IDF 为基础,使用向量模型或者概率模型等更复杂的算法来打分。比如说,概率模型中的 BM25(Best Matching 25)算法,这个经典算法就可以看作是 TF-IDF 算法的一种升级。在 Lucene 和 Elastic Search 这些搜索框架,以及 Google 这类常见的搜索引擎中,就都支持 BM25 排序。
- 基础权重
BM25 算法认为词频和相关性的关系并不是线性的。即,随着词频的增加,相关性的增加会越来越不明显,并且还会有一个阈值上限。当词频达到阈值以后,那相关性就不会再增长了。因此,BM25 对于 TF 的使用,设立了一个公式,如下: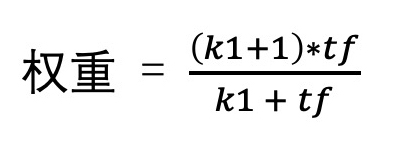
在这个公式中,随着 tf 的值逐步变大,权重会趋向于 k1 + 1 这个固定的阈值上限(将公式的分子分母同时除以 tf,就能看出这个上限)。其中,k1 是可以人工调整的参数。k1 越大,权重上限越大,收敛速度越慢,表示 tf 越重要。在极端情况下,也就是当 k1 = 0 时,就表示 tf 不重要。比如,在下图中,当 k1 = 3 就比 k1 = 1.2 时的权重上限要高很多。那按照经验来说,我们会把 k1 设为 1.2 。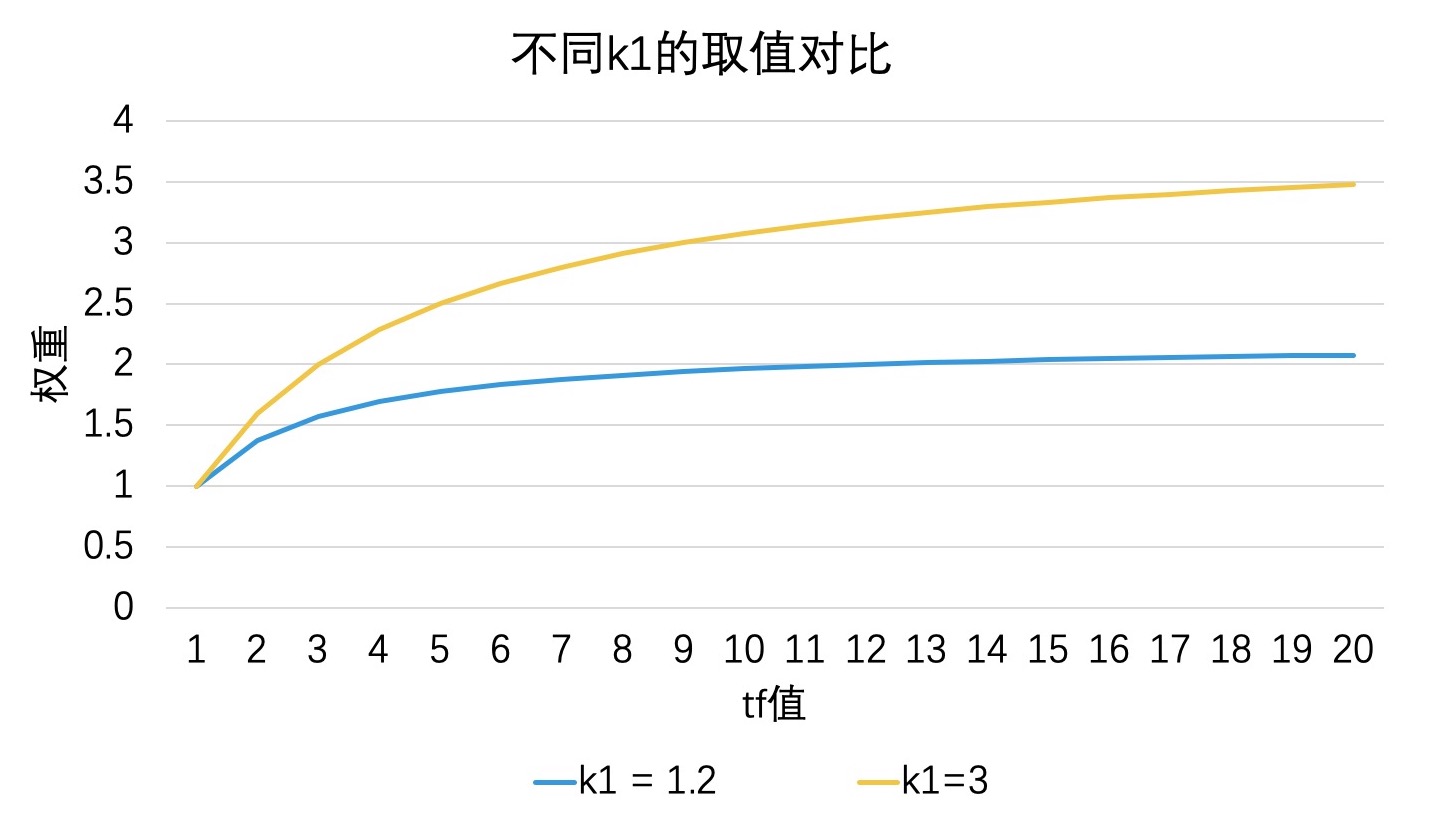
文档中词项权重
除了考虑词频,BM25 算法还考虑了文档长度的影响,也就是同样一个词项,如果在两篇文档中出现了相同的次数,但一篇文档比较长,而另一篇文档比较短,那一般来说,短文档中这个词项会更重要。这个时候,我们需要在上面的公式中,加入文档长度相关的因子。那么,整个公式就会被改造成如下的样子:

l 越长,分母中的 k1 就会越大,整体的相关性权重就会越小。b代表了文档长度的重要性,可以人工调整,它的取值范围是 0 到 1。当 b 取 0 时,我们可以完全不考虑文档长度的影响;而当 b 取 1 时,k1 的重要性要按照文档长度进行等
比例缩放。按照经验,我们会把 b 设置为 0.75,这样的计算效果会比较好。查询词中词项权重
除此以外,如果查询词比较复杂,比如说一个词项会重复出现,那我们也可以把它看作是一个短文档,用类似的方法计算词项在查询词中的权重。举个例子,如果我们的查询词是“极客们的极客时间课程”,那么“极客”这个词项,其实在查询词中就出现了两次,它的权重应该比“时间”“课程”这些只出现一次的词项更重要。因此,BM25 对词项在查询词中的权重计算公式如下:

其中 tfq表示词项在查询词 q 中的词频,而 k2 是可以人工调整的参数,它和 k1 的参数作用是类似的。由于查询词一般不会太长,所以词频也不会很大,因此,我们没必要像对待文档一下,用 k1 = 1.2 这么小的范围对它进行控制。我们可以放大词频的作用,把 k2 设置在 0~10 之间。极端情况下,也就是当 k2 取 0 时,表示我们可以完全不考虑查询词中的词项权重。BM25算法的具体相关性算分
其实,我们可以回顾一下标准的 TF-IDF,把其中的 TF 进行扩展,变为“文档中词项权重”和“查询词中词项权重”的乘积。这样,我们就得到了 BM25 算法计算一个词项和指定文档相关性的打分公式,它由 IDF、文档中词项权重以及查询词中词项权重这三部分共同组成。公式如下: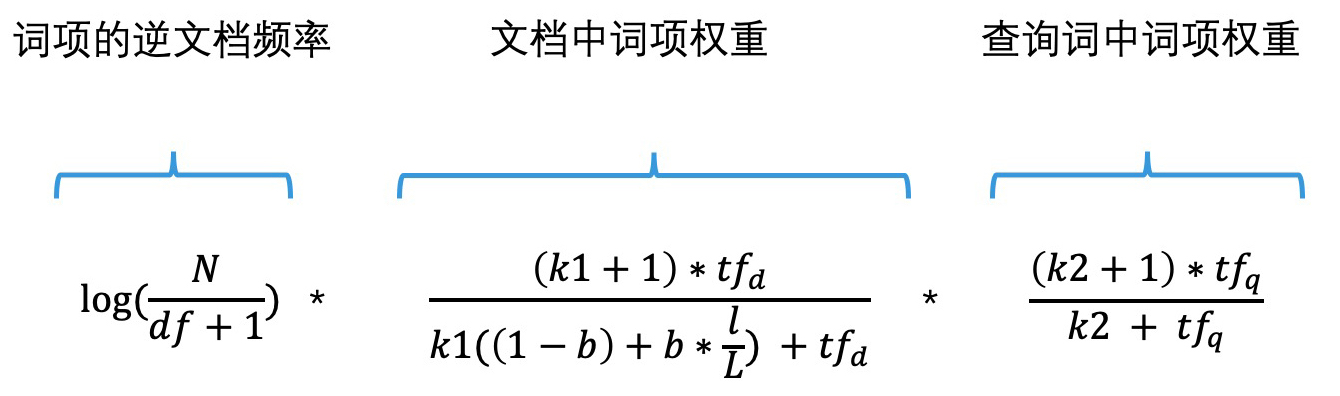
如果一个查询词 q 中有多个词项 t,那我们就要把每一个词项 t 和文档 d 的相关性都计算出来,最后累加。这样,我们就得到了这个查询词 q 和文档 d 的相关性打分结果,我们用 score(q,d) 来表示,公式如下: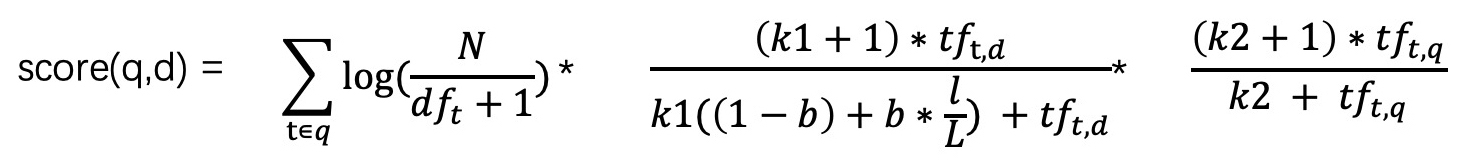
这就是完整的 BM25 算法的表达式了。它其实就是对 TF-IDF 的算法中的 TF 做了更细致的处理而已。其实,BM25 中的 IDF 的部分,我们也还可以优化,比如,基于二值独立模型对它进行退化处理(这是另一个分析相关性的模型,这里就不具体展开说了)之后,我们就可以得到一个和 IDF 相似的优化表示,你可以将它视为 IDF 的变体,用来替换公式中原有的 IDF 部分。公式如下: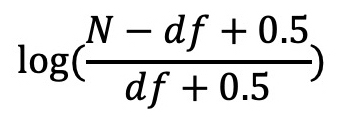
总结来说,BM25 算法就是一个对查询词和文档的相关性进行打分的概率模型算法。BM25 算法考虑了四个因子,分别为 IDF、文档长度、文档中的词频以及查询词中的词频。并且,公式中还加入了 3 个可以人工调整大小的参数,分别是 :k1、k2 和 b。
使用 机器学习 进行打分
随着搜索引擎的越来越重视搜索结果的排序和效果,我们需要考虑的因子也越来越多。比如说,官方的网站是不是会比个人网页在打分上有更高的权重?用户的历史点击行为是否也是相关性的一个衡量指标?
在当前的主流搜索引擎中,用来打分的主要因子已经有几百种了。如果我们要将这么多的相关因子都考虑进来,再加入更多的参数,那 BM25 算法是无法满足我们的需求的。
- 机器学习的打分原理简述
机器学习的打分原理其实就是把不同的打分因子进行加权求和。
比如说,有 n 个打分因子,分别为 x1到 xn,而每个因子都有不同的权重,我们记为 w1到 wn,那打分公式就是:
Score = w1 x1+ w2 x2+ w3 x3+ …… + wn xn
公式中的权重要如何确定呢?这就需要我们利用训练数据,让机器学习在离线阶段,自动学出最合适的权重。这样,就避免了人工制定公式和权重的问题。当然,这个打分公式是不能直接使用的,因为它的取值范围是负无穷到正无穷。这是一个跨度很广的范围,并不好衡量和比较相关性。一般来说,我们会使用 Sigmoid 函数对 score 进行处理,让它处于 (0,1) 范围内。Sigmoid 函数的取值范围是(0,1),它的函数公式和图像如下所示: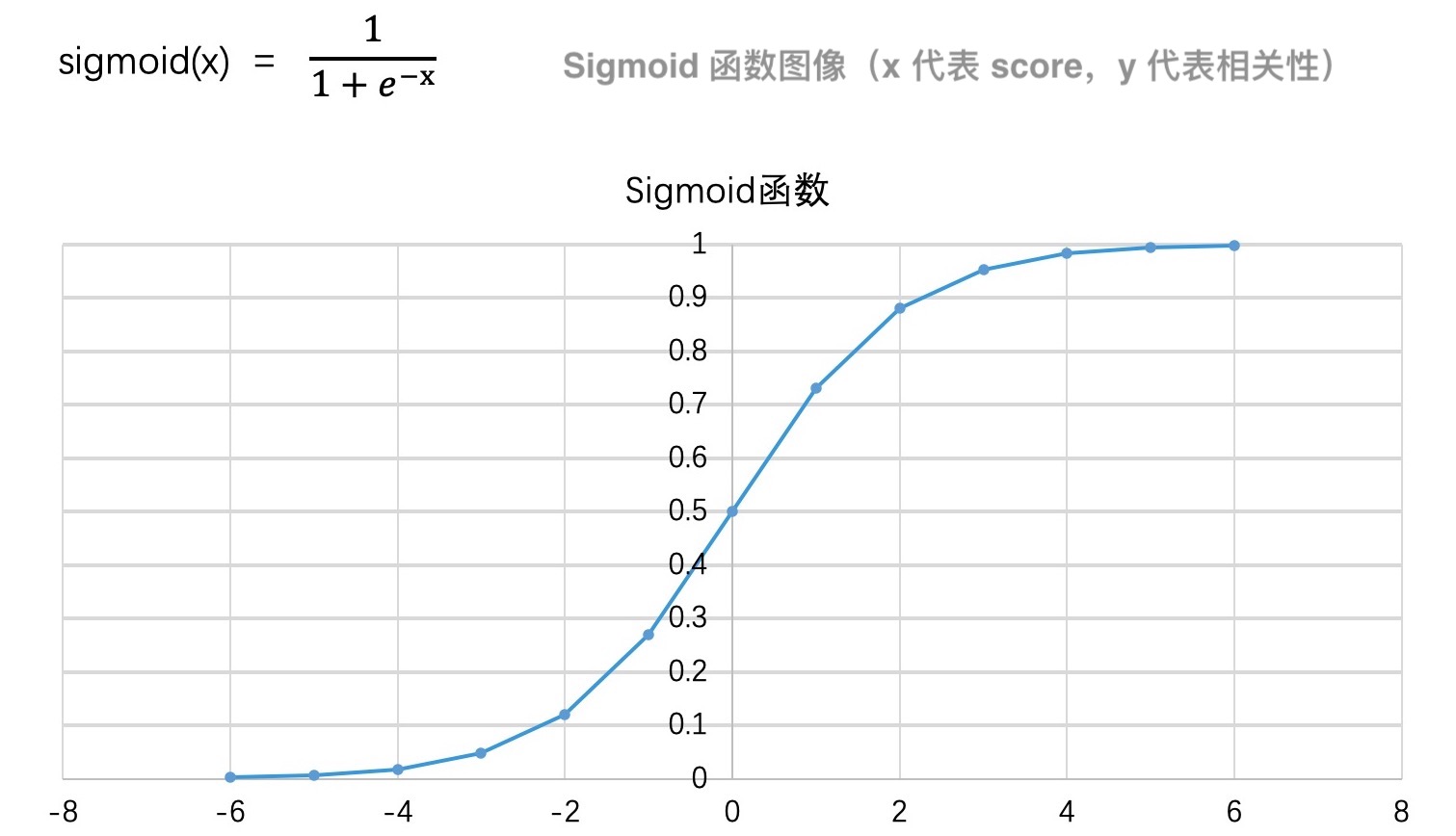
Sigmoid 函数的特点就是:x 值越大,y 值越接近于 1;x 值越小,y 值越接近于 0。并且,x 值在中间一段范围内,相关性的变化最明显,而在两头会发生边际效应递减的现象,这其实也符合我们的日常经验。比方说,一个 2-3 人的项目要赶进度,一开始增加 1、2 个人进来,项目进度会提升明显。但如果我们再持续加人进来,那项目的加速就会变平缓了。
这个打分方案,就是工业界常见的逻辑回归模型(Logistic Regression)(至于为什么逻辑回归模型的表现形式是 Sigmoid 函数,这是另一个话题,这里就不展开说了)。当然,工业界除了逻辑回归模型的打分方案,还有支持向量机模型、梯度下降树等。并且,随着深度学习的发展,也演化出了越来越多的复杂打分算法,比如,使用深度神经网络模型(DNN)和相关的变种等。由于机器学习和深度学习是专门的领域,因此相关的打分算法我就不展开了。在这一讲中,你只要记住,机器学习打分模型可以比人工规则打分的方式处理更多的因子,能更好地调整参数就可以了。
如何根据打分结果快速进行 Top K 检索?
在给所有的文档打完分以后,接下来,我们就要完成排序的工作了。一般来说,我们可以使用任意一种高效的排序算法来完成排序,比如说,我们可以使用快速排序,它排序的时间代价是 O(n log n)。但是,我们还要考虑到,搜索引擎检索出来结果的数量级可能是千万级别的。在这种情况下,即便是 O(n log n) 的时间代价,也会是一个非常巨大的时间损耗。
那对于这个问题,我们该怎么优化呢?其实,在实际系统中,因为,互联网时代的数据检索应该通过相似度算法提高检索结果与用户期望的符合度,而不应该让用户在检索结果中自己挑选满意的数据,如果用户翻了多页过后还是没能找到满意的结果,那么这个搜索引擎应该是失败的。所以,我们不需要返回所有结果,只需要返回 Top K 个结果就可以。这就是许多大规模检索系统应用的的 Top K 检索了。而且,我们前面的打分过程都是非常精准的,所以我们今天学习的也叫作精准 Top K 检索。
- 优化排序
由于只需要选取 Top K 个结果,因此我们可以使用堆排序来代替全排序。这样我们就能把排序的时间代价降低到 O(n) + O(k log n)(即建堆时间 + 在堆中选择最大的 k 个值的时间),而不是原来的 O(n log n)。举个例子,如果 k 是 1000,n 是 1000 万,那排序性能就提高了近 6 倍!这是一个非常有效的性能提升。
总结
首先,我们讲了 3 种打分方法,分别是经典算法 TF-IDF、概率模型 BM25 算法以及机器学习打分。
在 TF-IDF 中, TF 代表了词项在文档中的权重,而 IDF 则体现了词项的区分度。尽管 TF-IDF 很简单,但它是许多更复杂的打分算法的基础。比如说,在使用机器学习进行打分的时候,我们也可以直接将 TF-IDF 作为一个因子来处理。
BM25 算法则是概率模型中最成功的相关性打分算法。它认为 TF 对于相关性的影响是有上限的,所以,它不仅同时考虑了 IDF、文档长度、文档中的词频,以及查询词中的词频这四个因子, 还给出了 3 个可以人工调整的参数。这让它的打分效果得到了广泛的认可,能够应用到很多检索系统中。
不过,因为机器学习可以更大规模地引入更多的打分因子,并且可以自动学习出各个打分因子的权重。所以,利用机器学习进行相关性打分,已经成了目前大规模检索引擎的标配。
完成打分阶段之后,排序阶段我们要重视排序的效率。对于精准 Top K 检索,我们可以使用堆排序来代替全排序,只返回我们认为最重要的 k 个结果。这样,时间代价就是 O(n) + O(k log n) ,在数据量级非常大的情况下,它比 O(n log n) 的检索性能会高得多。
讨论
- 在今天介绍的精准 Top K 检索的过程中,你觉得哪个部分是最耗时的?是打分还是排序?
- 你觉得机器学习打分的优点在哪里?你是否使用过机器学习打分?可以把你的使用场景分享出来。
答:
1. 耗时的步骤其实是打分,因此,我们如果想加快检索效率的话,如何优化打分过程就是一个很重要的方向。
2. 其实机器学习的关键就是寻找因子(也就是特征),以及学习权重的过程。对于机器学习和特征工程方向,这其实是另一个领域。可以把深度学习理解为“用数据推导规则”。实际上,无论是机器学习还是深度学习,目前其实离我们真正期待的智能还有一段距离,从文中的简单例子你可以看到,机器学习更多是基于巨大的算力,用数据去拟合出一个有限的规则表达式,这个学习出来的规则其实还有许多可完善的地方,比如说人脸识别,有人就做过实验,给一个五官完整,但是比例和位置一看就不对的人脸图像给模型识别,结果模型识别为“真人”。因此,在人工智能方向上,我们还需要再往前走。
问:
文档频率df,随着文档数量的增多,df应该会重新计算么?如果是需要重新计算,也需要批量更新所有文档的分数吧?
答:
对于df,的确会随着文档的增加而变化。因此是需要更新的。在倒排索引中,由于idf是和key存在一起的,因此,我们可以在文档变化时,对增量倒排索引的key中的idf值进行更新就可以了。不过要注意:如果使用了基于文档的水平拆分,那么增量索引只会在一个分片中生效。这样如果持续久了,idf值会不准,相关性计算精度会下降。因此,需要周期性地重构全量索引。

