What
状态检索,快速判断一个值是否存在
布隆过滤器的原理是,当一个元素被加入集合时,通过K个散列函数将这个元素映射成一个位数组中的K个点,把它们置为1。检索时,我们只要看看这些点是不是都是1就(大约)知道集合中有没有它了:如果这些点有任何一个0,则被检元素一定不在;如果都是1,则被检元素很可能在。这就是布隆过滤器的基本思想。
How
提高查询效率
使用数组的随机访问特性来提高查询效率
如果我们要查询的对象 ID 本身是正整数类型,而且 ID 范围有上限的话。我们就可以申请一个足够大的数组,让数组的长度超过 ID 的上限。然后,把数组中所有位置的值都初始化为 0。对于存在的用户,我们直接将用户 ID 的值作为数组下标,将该位置的值从 0 设为 1 就可以了。
- 存在的问题:
如果 ID 的范围比较广,比如说在 10 万之内,那我们就需要保证数组的长度大于 10 万。所以,这种方案的占用空间会很大。而且,如果这个数组是一个 int 32 类型的整型数组,那么每个元素就会占据 4 个字节,用 4 个字节来存储 0 和 1 会是一个巨大的空间浪费。
减少存储空间
使用位图来减少存储空间
使用最少字节的类型来定义数组。比如说,使用 1 个字节的 char 类型数组,或者使用 bool 类型的数组(在许多系统中,一个 bool 类型的元素也是 1 个字节)。它们和 4 个字节的 int 32 数组相比,空间使用效率提升了 4 倍,这已经算是不错的改善了。但是,使用 char 类型的数组,依然是一个非常“浪费空间”的方案。因为表示 0 或者 1,理论上只需要一个 bit。所以,如果我们能以 bit 为单位来构建这个数组,那使用空间就是 int 32 数组的 1/32,从而大幅减少了存储使用的内存空间。这种以 bit 为单位构建数组的方案,就叫作 Bitmap,翻译为位图。
位图的优势非常明显,但许多系统中并没有以 bit 为单位的数据类型。因此,我们往往需要对其他类型的数组进行一些转换设计,使其能对相应的 bit 位的位置进行访问,从而实现位图。
- 其它数据类型转换为位图的思想:
以char类型为例,一个char占8bit,则char类型的数组中的每个元素可以存放8个位图元素,也就是可以表示8个状态信息。如果某个id为11,理论上该id对应的状态信息存储在位图数组的第11个元素中,实际也就是位于char类型数组的 第2个元素中的第3个bit(11%8 = 1…3)。对于第2个元素的访问直接使用数组下标[1]就可以在 O(1) 的时间内访问到。对于第 2 个元素中的第 3 个 bit 的访问,我们可以通过位运算,先构造一个二进制为 00100000 的字节(字节的第 3 位为 1),然后和第 1个元素做 and 运算,就能得知该元素的第 3 位是 1 还是 0。这也是一个时间代价为 O(1) 的操作。这样一来,通过两次 O(1) 时间代价的查找,我们就可以知道第 11 个 bit 的值是 0 还是 1 了。如下图:
最终方案
利用布隆过滤器实现最终方案
一个数组所占的空间其实就是“数组元素个数 * 单个元素大小”,利用位图可以缩小单个元素大小。而使用hash函数则可以限制数组长度。使用哈希函数也带来了另一个优点,那就是我们不需要把用户 ID 限制为正整数了,它也可以是字符串。这样一来,压缩数组长度,并使用哈希函数,就是一个更加通用的解决方案。
- 布隆过滤器:
主要思想也就是使用开放寻址法中的双散列优化方案。最大的特点,就是对一个对象使用多个哈希函数。如果我们使用了 k 个哈希函数,就会得到 k 个哈希值,也就是 k 个下标,我们会把数组中对应下标位置的值都置为 1。
- 布隆过滤器 vs 位图:
布隆过滤器不再使用1个bit来表示一个对象,而是使用 k个bit 位来表示一个对象。这样两个对象的 k 位都相同的概率就会大大降低,从而能够解决哈希冲突的问题了。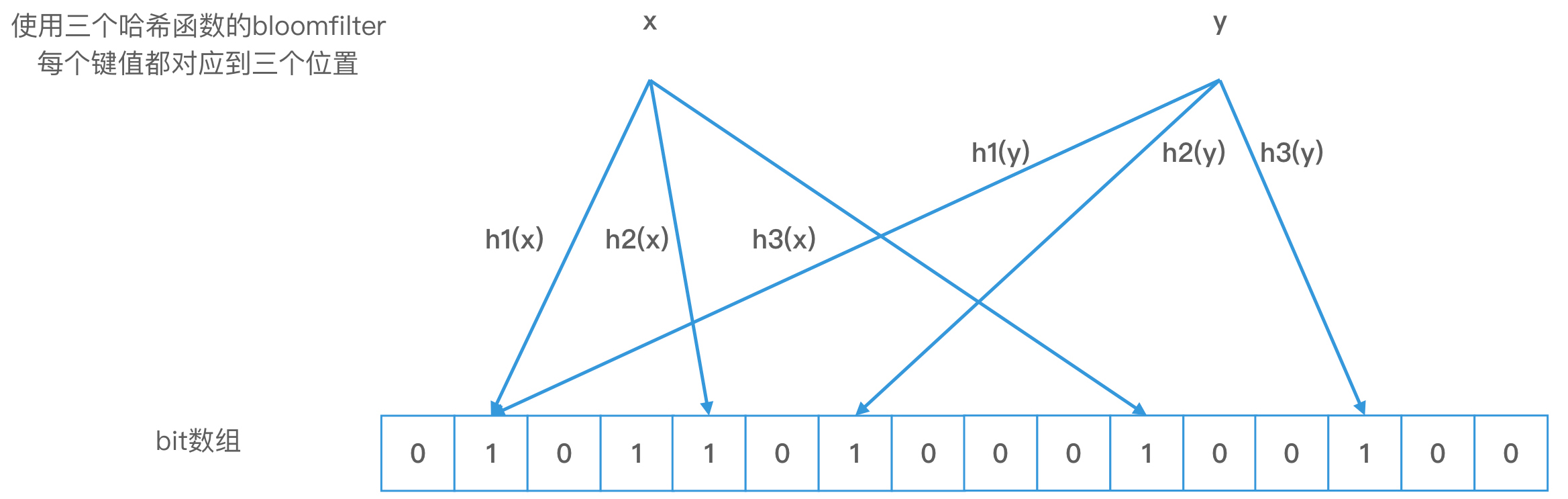
但是,布隆过滤器的查询有一个特点,就是即使任何两个元素的哈希值不冲突,而且我们查询对象的 k 个位置的值都是 1,查询结果为存在,这个结果也可能是错误的。这就叫作布隆过滤器的错误率。
- 示例
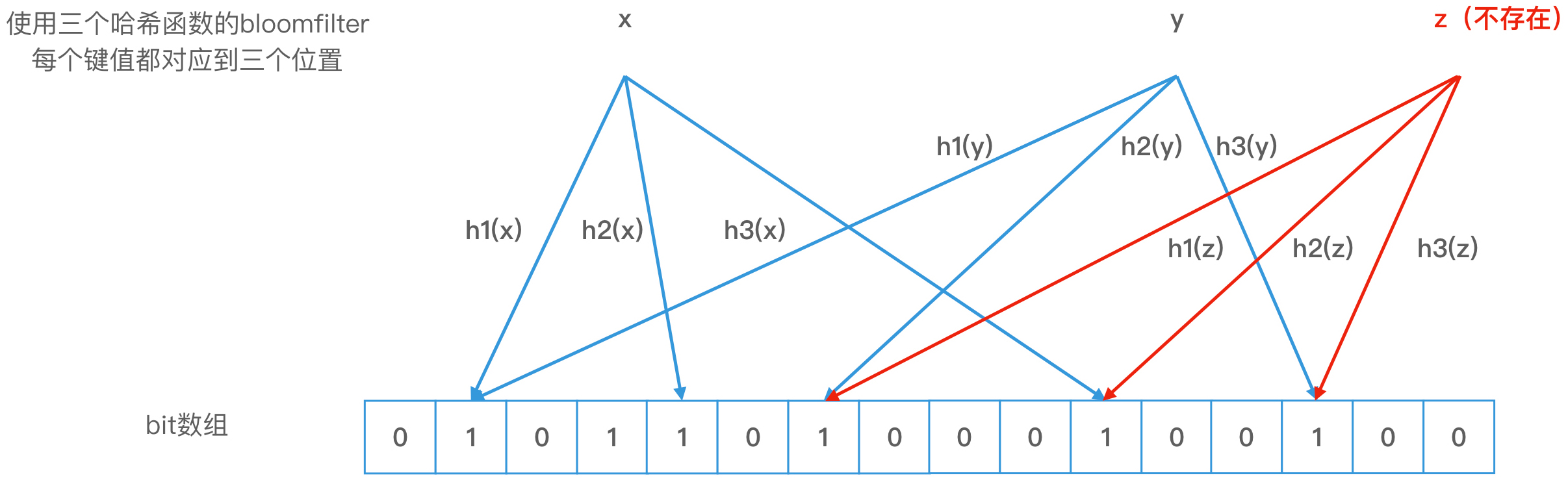
我们可以看到,布隆过滤器中存储了 x 和 y 两个对象,它们对应的 bit 位被置为 1。当我们查询一个不存在的对象 z 时,如果 z 的 k 个哈希值的对应位置的值正好都是 1,z 就会被错误地认定为存在。而且,这个时候,z 和 x,以及 z 和 y,两两之间也并没有发生哈希冲突。那遇到“可能存在”这样的情况,一般以存在的情况考虑即可。所以布隆过滤器只能准确判断数据的不存在性,而无法准确判断其存在性。
如果哈希函数的个数不合理,比如哈希函数越少,布隆过滤器的错误率就会越大。因此,除了使用多个哈希函数避免哈希冲突以外,我们还要控制布隆过滤器中哈希函数的个数。有这样一个计算最优哈希函数个数的数学公式: 哈希函数个数 k = (m/n) * ln(2)。其中 m 为 bit 数组长度,n 为要存入的对象的个数。实际上,如果哈希函数个数为 1,且数组长度足够,布隆过滤器就可以退化成一个位图。所以,我们可以认为“位图是只有一个特殊的哈希函数,且没有被压缩长度的布隆过滤器”。

