本质上是:使用非线性的树状结构来改造有序链表,让链表也具有二分查找的能力。
树
把链表中间节点 M 拎出来单独记录,链表便可实现以 O(1) 的时间代价访问中间节点。然后,我们判断这个节点和要查找的元素是否相等。相等,则返回查询结果。如果节点元素大于要查找的元素,那我们就到左边的部分继续查找;反之,则在右边部分继续查找。对于左边或者右边的部分,我们可以将它们视为两个独立的子链表,依然沿用这个逻辑。示意图如下:

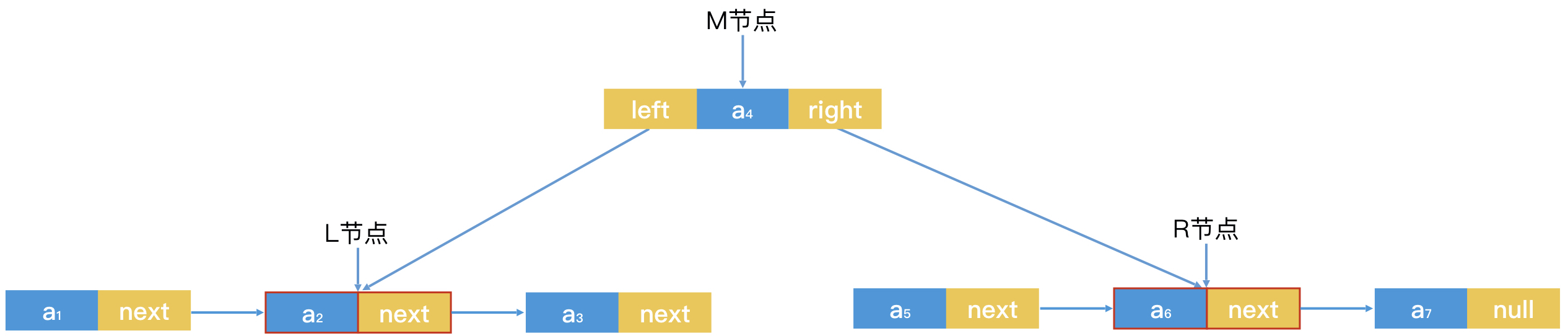
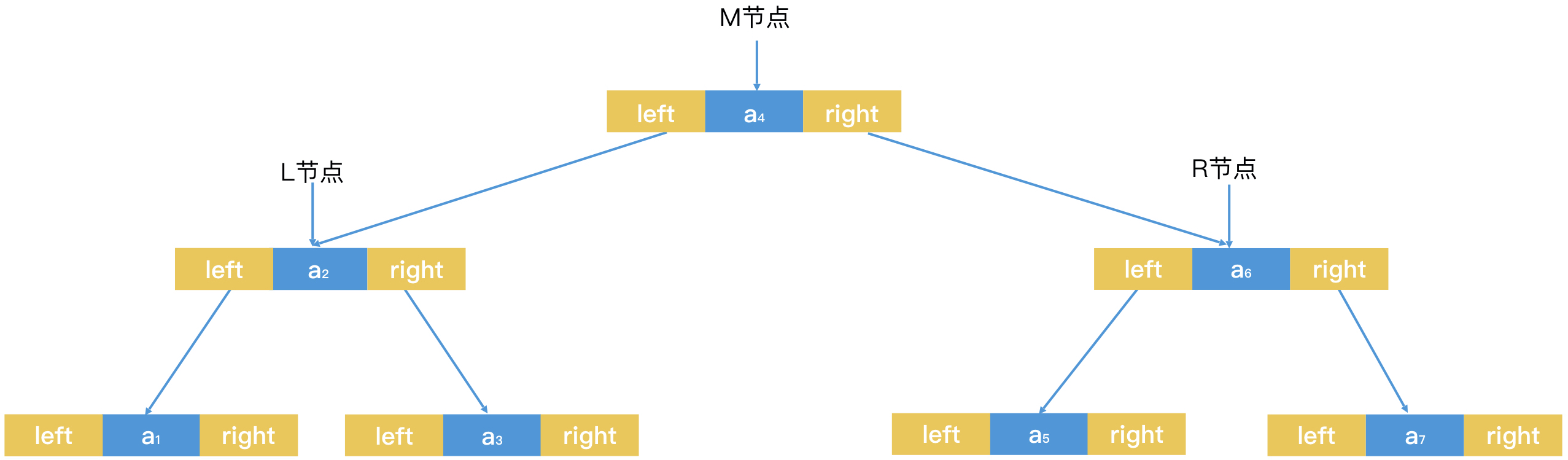
没错,这就是我们常见的二叉树,而且还是有序二叉树,它的左子树的所有节点的值都小于根节点,同时右子树所有节点的值都大于等于根节点。这样的有序结构,使得它能使用二分查找算法,快速地过滤掉一半的数据。具备了这样特点的二叉树,就是二叉检索树(Binary Search Tree),或者叫二叉排序树(Binary Sorted Tree)。
二叉检索树的检索空间平衡方案:
二叉检索树的检索时间代价一定是 O(log n) 吗?其实不一定。假设,一个二叉树的每一个节点的左指针都是空的,右子树的值都大于根节点。那么它满足二叉检索树的特性,是一颗二叉检索树。但是,如果我们把左边的空指针忽略,你会发现它其实就是一个单链表!单链表的检索效率如何呢?其实是 O(n),而不是 O(log n)。因此,为了提升检索效率,我们应该尽可能地保证二叉检索树的平衡性,让左右子树尽可能差距不要太大。这样无论我们是继续往左边还是右边检索,都可以过滤掉一半左右的数据。
也正是为了解决这个问题,有更多的数据结构被发明了出来。比如:AVL 树(平衡二叉树)和红黑树,其实它们本质上都是二叉检索树,但它们都在保证左右子树差距不要太大上做了特殊的处理,保证了检索效率,让二叉检索树可以被广泛地使用。比如,我们常见的 C++ 中的 Set 和 Map 等数据结构,底层就是用红黑树实现的。
- 跳表
在节点上增加一个指针,指向更远的节点。同理,增加更多的指针,提供不同步长的遍历能力,比如一次跳过 4 个节点,甚至一半的节点,那我们就可以更快速地访问到中间节点了。这样的数据结构就是跳表(Skip List)。
理想的跳表,从链表头开始,用多个不同的步长,每隔 2^n 个节点做一次直接链接(n 取值为 0,1,2……)。跳表中的每个节点都拥有多个不同步长的指针,我们可以在每个节点里,用一个数组 next 来记录这些指针。next 数组的大小就是这个节点的层数,next[0]就是第 0 层的步长为 1 的指针,next[1]就是第 1 层的步长为 2 的指针,next[2]就是第 2 层的步长为 4 的指针,依此类推。你会发现,不同步长的指针,在链表中的分布是非常均匀的,这使得整个链表具有非常平衡的检索结构。如下图:
举个例子,当我们要检索 k=a6时,从第一个节点 a1开始,用最大步长的指针开始遍历,直接就可以访问到中间节点 a5。但是,如果沿着这个最大步长指针继续访问下去,下一个节点是大于 k 的 a9,这说明 k 在 a5和 a9之间。那么,我们就在 a5和 a9之间,用小一个级别的步长继续查询。这时候,a5的下一个元素是 a7,a7依然大于 k 的值,因此,我们会继续在 a5和 a7之间,用再小一个级别的步长查找,这样就找到 a6了。这个过程其实就是二分查找。时间代价是 O(log n)。
跳表的平衡方案:
当我们要在跳表中插入元素时,节点之间的间隔距离就被改变了。如果要保证理想链表的每隔 2^n 个节点做一次链接的特性,我们就需要重新修改许多节点的后续指针,这会带来很大的开销。所以,在实际情况下,我们会在检索性能和修改指针代价之间做一个权衡。为了保证检索性能,我们不需要保证跳表是一个“理想”的平衡状态,只需要保证它在大概率上是平衡的就可以了。因此,当新节点插入时,我们不去修改已有的全部指针,而是仅针对新加入的节点为它建立相应的各级别的跳表指针。具体的操作过程如下:
首先,我们需要确认新加入的节点需要具有几层的指针。可通过随机函数来生成层数,通过随机生成指针层数的方式,我们就可以保证指针的分布,在大概率上是平衡的。在确认了新节点的层数 n 以后,接下来,我们需要将新节点和前后的节点连接起来,也就是为每一层的指针建立前后连接关系。其实每一层的指针链接,你都可以看作是一个独立的单链表的修改,因此我们只需要用单链表插入节点的方式完成指针连接即可。 如下图:
通过这样一种方式,我们可以大大减少修改指针的代价。当然,由于新加入节点的层数是随机生成的,因此在节点数目较少的情况下,如果指针分布的不合理,检索性能依然可能不高。但是当节点数较多的时候,指针会趋向均匀分布,查找空间会比较平衡,检索性能会趋向于理想跳表的检索效率,接近 O(log n)。
因此,相比于复杂的平衡二叉检索树,如红黑树,跳表用一种更简单的方式实现了检索空间的平衡。并且,由于跳表保持了链表顺序遍历的能力,在需要遍历功能的场景中,跳表会比红黑树用起来更方便。这也就是为什么,在 Redis 这样的系统中,我们经常会利用跳表来代替红黑树作为底层的数据结构。

