2.2 数制的概念
数制:通常是指进位计数制(做加法的时候逢几进一的数制)
进位计数制:就是做加法的时候逢几进一的数制。比如说:十进制:逢十进一、二进制:逢二进一。
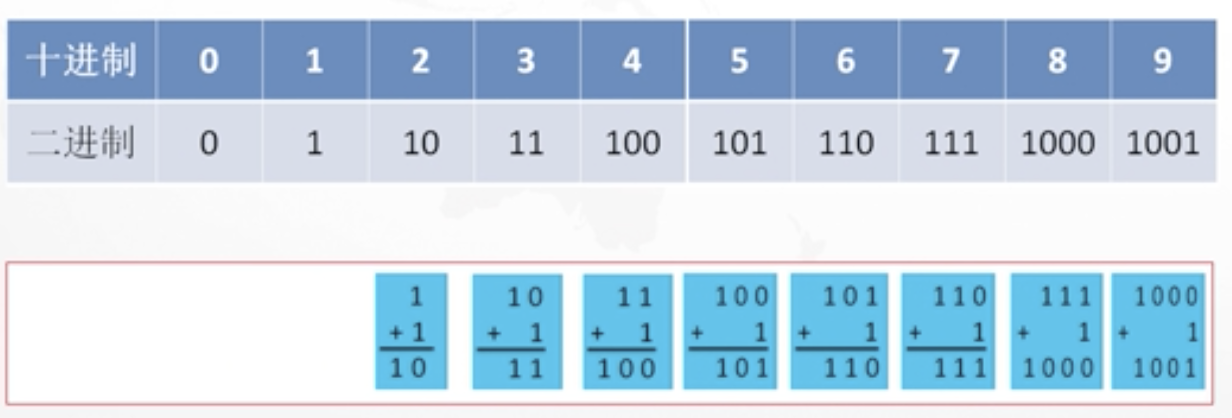
十进制和二进制的对照计算表
二进制的缺点
太长了
一个比较大的十进制,转换成二进制后占很多位。比如上表的9:一位十进制就占了4位二进制
难认、难记、难算
进位计数制:2、8、10、16

名词解析:
- 基本数符:也就是基本符号
- 八进制的角标:O,也因为大写的“O”容易和数字“0”混淆,所以也用“Q”来表示
- 十六进制:本应该有16个基本符号0-15的。但是10-15需要用一位来表示,所以用A-F分别表示10-15
角标
二进制:B
八进制:O
十进制:D
十六进制:H值域
3位二进制数:000~111 (2个取值)也就是表示0~7的数
1位八进制数:0~7 (8个取值)
因为二的3次方等于八的1次方, 所以每3位二进制数可以转换成1位八位进制数。也就是说3位二进制数和1位八进制数是可以等值转换的。
同理:因为二的4次方等于十六的1次方,所以每4位二进制数可以转换为1位十六进制数。数值计算公式
怎么分辨出一个数的大小是(十进制的)多少?
数值中每个数符表示的值应该等于数符本身乘以他所在位的权值。(以345.12为例,数值就是345.12,数符就是3、4、5等)位
给数值中的每一位进行命名。
命名的规则是:以小数点为分割,向左分别是D0位、D1位……依次增大,向右分别是D-1位、D-2位……依次减小。
给数值中的每一位起了一个唯一的名字。讨论与思考(数位命名):为什么对数位命名时,个位命名为D0,而不是D1?
因为计算机中二进制、八进制、十六进制都是从0开始的。最小数字为0。权值(又称:单位值)
数制中某一位的单位值称为该位的权。(单位值,实际上指得就是1。比如:速度是单位时间内的里程数。单位时间指的是1小时/1秒钟。对照数学中的单位值,就是1。)
如何看某一位上的权值是多少,只要往这个位上放一个1,看他表示的是多少。
比如:345.12中,D2位的3表示的就是300。因为只要在D2位上放一个1,就表示100。这就是D2位的单位值、又称作D2位的权值。
那么,为什么D2位的权值是100呢?这个100单位值是怎么算出来的呢?换句话说,单位值、权值是怎么算出来的呢?这就要说到权值公式了:
权值公式(单位值公式)
对于r进制,其Dn的权值等于r的n次方:D**n = rn**
对于10进制,其D2位的权值等于10的2次方
十进制计算公式举例
以数字 321.45 为例:
| 位 | D2 | D1 | D0 | . | D-1 | D-2 | 求解结果 |
|---|---|---|---|---|---|---|---|
| 数 | 3 | 2 | 1 | . | 4 | 5 | |
| 权值公式 | 102 | 101 | 100 | - | 10-1 | 10-2 | |
| 权值 | 100 | 10 | 1 | - | -10 | -100 | |
| 解析 | 3*102 | 2*101 | 1*100 | - | 4*10-1 | 5*10-2 | |
| 结果 | 3*100+ | 2*10+ | 1*1+ | - | 4*-10+ | 5*-100+ | 321.45D |
数值判定的方法:按权展开(当前位的数值与权值相乘),相加求和。
综上,多项式求和如下
321.45 = 310+210+110+410+5*10
对于我们不熟悉的数,怎么计算其大小?同样用这个方法,按权展开、相加求和:
二进制转成十进制计算公式举例
以数字 10111B 为例:
| 位 | D4 | D3 | D2 | D1 | D0 | 求解结果 |
|---|---|---|---|---|---|---|
| 数 | 1 | 0 | 1 | 1 | 1 | |
| 权值公式 | 24 | 23 | 22 | 21 | 20 | |
| 权值 | 16 | 8 | 4 | 2 | 1 | |
| 解析 | 1*2 | 0*2 | 1*2 | 1*2 | 1*2 | |
| 结果 | 1*16+ | 0*8+ | 1*4+ | 1*2+ | 1*1+ | 23D |
求解:按权展开,相加求和。多项式求和10111B结果如下(B是二进制角标,表示前边是一个二进制数)
10111B = 12+02+12+12+12 = 23D (D是十进制角标,表示前面是一个十进制数)
别忘了用位上的数值r
总结:按权值转其他进制为十进制数
按权相乘,多项求和:按权展开每一项(数值*权值),多项之间的乘积相加求和。
对任意数制中的数按权值展开成多项式求和,就是在把他转换成十进制数。
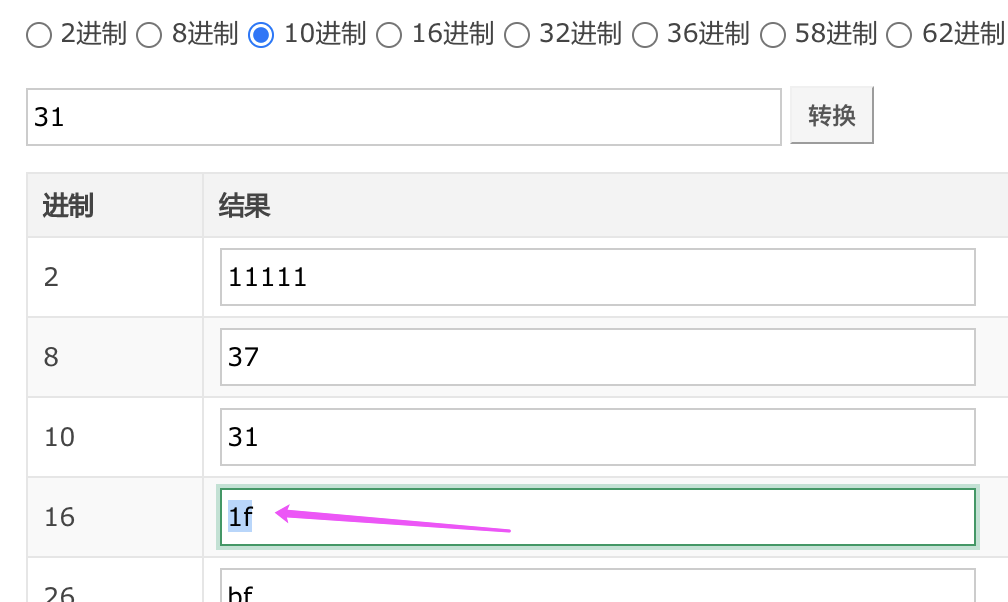
十六进制转十进制举例:
16进制的「1F」转成十进制的推算:
| 位 | D1 | D0 | 求解结果 |
|---|---|---|---|
| 数 | 1 | F | |
| 权值公式 | 161 | 160 | |
| 权值结果 | 16 | 1 | |
| 解析 | 1*161 | 15*160 | |
| 结果 | 1*16+ | 15*1+ | 31D |
2.3 数制转换
在线工具:https://tool.lu/hexconvert/ (用于验证)
把一个数转换成其他计数形式。比如把2进制转换为10进制,把16进制转换为2进制等。
二进制的(10111)等同于十进制的(23)只不过是一个数的不同形式之间进行转换而已。
**
数制转换的三种情况:
- R进制转换为十进制:把非十进制数按权值展开成多项式求和即可(数值与权值相乘,多项之间相加求和。详细做法见上边第二节)计算的结果就是十进制数形式。
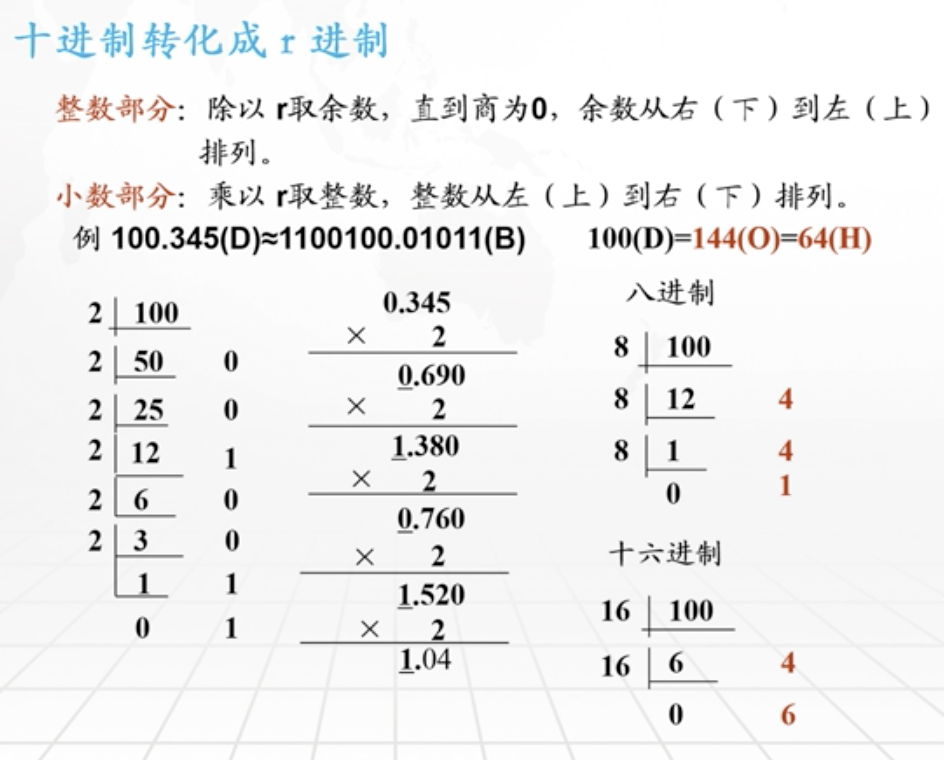
- 十进制转换为R进制:
- 不带小数点:数值除以目标进制,得到商以后继续除以目标进制,直到商为0。然后反转得到的余数顺序后排列所有余数。
- 带小数点:小数点左侧(整数部分)同上一条。小数点右侧(小数部分):小数部分数值乘以目标进制取整数,直到乘积的小数位变成0。最后按照所取整数按顺序排列放到小数位。
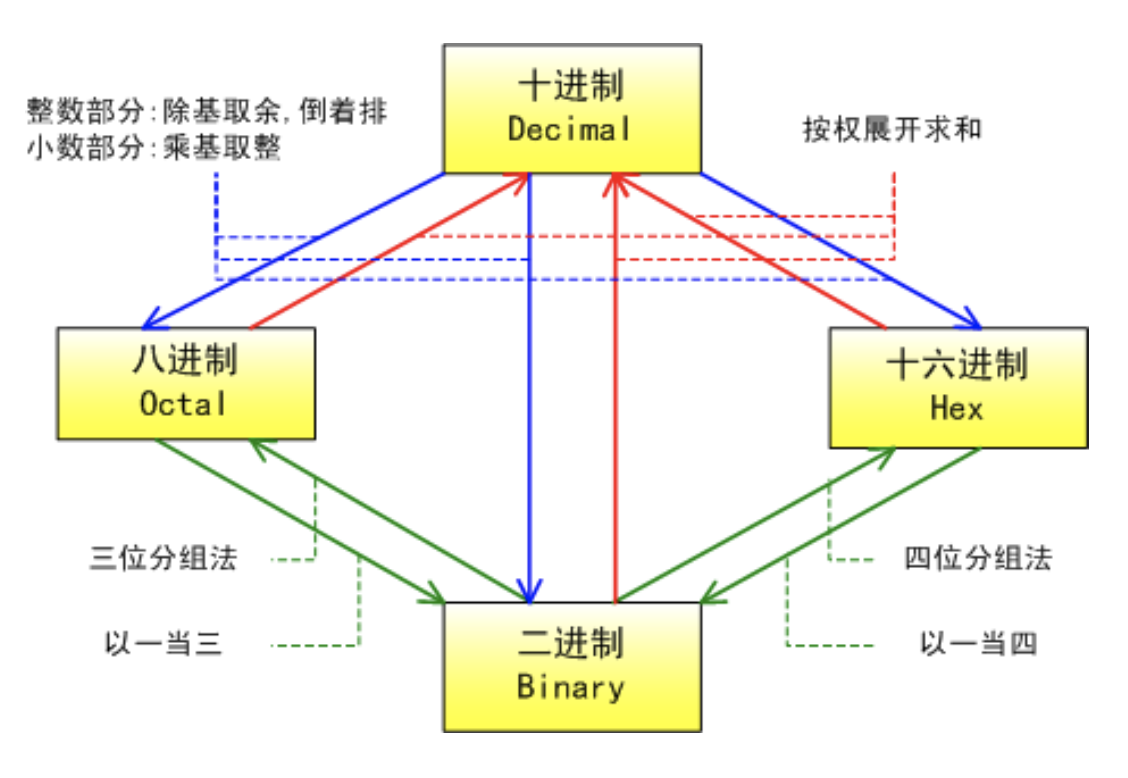
- 二进制和八进制、十六进制之间的转换:3位二进制算1位八进制,4位二进制算一位十六进制。反之依然。
R进制转换为十进制
贴一张看不懂的图:
基本思路:按权展开成多项式求和(数码乘以各自的权的累加求和)

注意⚠️:这种方法适用于转换成任何进制。
但是因为我们求和的时候,是按照十进制的加法运算规则进行计算的。所以得到的结果是十进制。
假如我们求和的时候,采用八进制运算规则求和,那么得到的结果就是八进制数。如下图:
练习题:
将以下非十进制数转换为十进制数
【1011.01 B】
【B7.F H】
【372.6 O】
问题:小数点怎么算的?
- .01转换称十进制是0.25,不知道怎么计算的额【10除以2、100除以2】
- .F是十六的负一次方,百度结果是0.9375,不知道怎么计算的。【先算16-1 10除以16,得到0.625,然后乘以10的负一次方(0.1)得到0.0625】
十进制转换为 R进制
基本思路:对转换结果进行逐位判断
1、先把整数部分和小数部分分别进行转换
2、再把两部分的转换结果拼接起来
举例-整数部分
例1、先来看一个十进制的例子:234D 转为 十进制的数
根据整数部分逐位判断方法:
数值除以目标进制,得到商以后继续除以目标进制,直到商为0。然后反转得到的余数顺序后排列所有余数。
如下图:234、23、2分别除以10,最终商成为0以后。按照分别除以10得到的4、3、2按照倒序排列后成为2、3、4。进行整合得到最终结果234。
例2、再来看一个二进制的例子:50.25D转为 二进制数
二进制形式逐位判断的方法:
整数部分:除以2取余数,直到商为0,所取余数自下向上排列
小数部分:乘以2取整数,直到乘积的小数部分为0。所取整数按顺序排列
整数部分计算如下:数值除以目标进制2,得到的商一直除以2直到商为0。除以2过程中得到的余数0、1、0、0、1、1,按顺序排列后再翻转过来整合一起,得到目标二进制数:110010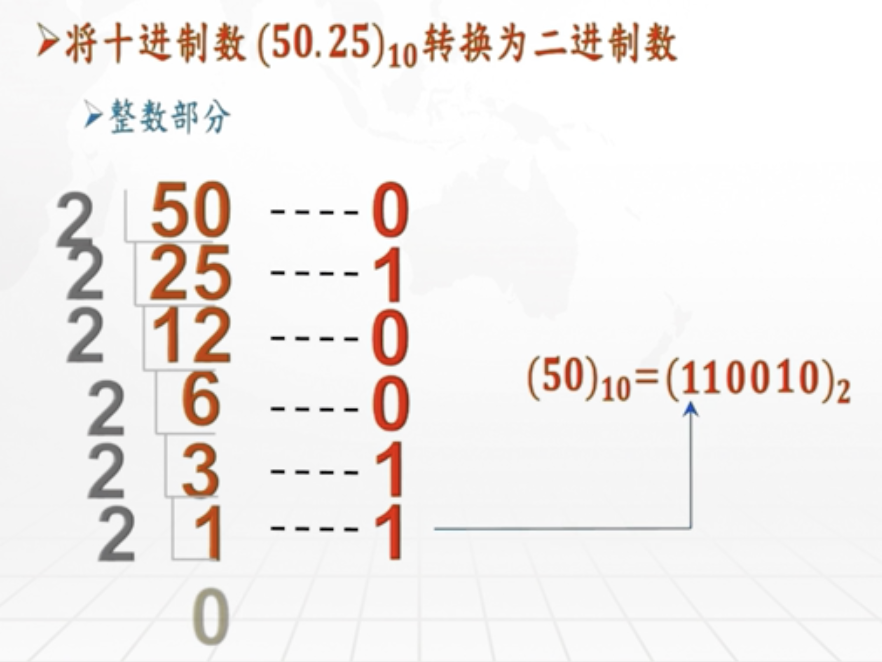
举例-小数部分
要想总结小数部分计算规律,先看如何分离出一个十进制纯小数的各个位。
方法是:乘以目标进制10,取整数,一直到乘积的小数部分为零。
例3、以0.25D为例转换为十进制:*
0.25 10 = 2.5, 取整得到2。留下0.5继续
0.5 * 10 = 5.0, 取整得到5,留下乘积的小数部分为0,结束。
最终,2、5按顺序排列,分别放到小数位的D-1、D-2位,就是0.25D
例4、以0.25D为例转换为二进制
0.25 2 = 0.5,取整得到0,留下0.5继续
0.5 2 = 1.0, 取整得到1,留下乘积的小数部分为0,结束
最终,0、1按顺序排列,分别放到小数位的D-1、D-2位,就是0.01B
总结:
小数值乘以目标进制取整数,所取整数按照顺序排列。直到乘积的小数位为0则停止。
所以,十进制数50.25D转换为二进制数计算结果如下:
整数部分:50D
50 / 2 = 25 … 0
25 / 2 = 12 … 1
12 / 2 = 6 … 0
6 / 2 = 3 … 0
3 / 2 = 1 … 1
1 / 2 = 0 … 1 商为0,停止🤚
商为0后,将余数倒叙排列:110010B
小数部分:0.25D
0.25 2 = 0.5 > 取整0。小数点位乘积不为零,继续
0.5 2 = 1.0 > 取整1。 小数点位乘积为零,停止🤚
小数点位乘积为零后,将取整的数按需排列到小数位:0.01B
整数结果与小数结果拼接,得到最终结果:110010.01 B
总结:
练习题
10101.101B = 21.625D(整数部分按权展开相加求和,得到21,小数部分2和2分别是0.5+0.125得到0.625)
75.43O = ?D
E2.1D H = ?D
127D = ?B = ?O = ?H
218.35D = ?B = ?O = ?H
答案:
1.(10101.101)B=( 21.625 )D。
2.(75.43)O=(61.546875)D
3.(E2.1D)H=( 226.1133 )D。
4.(127)D=(1111111)B=(177)O=(7F)H。
5.(218.35)D=(11011010.01011)B=(332.26)O=(DA.58)H。
我的问题:
十进制的437转换为十六进制的数,我计算了两遍都是bb5,但是在线工具验证的是1b5,不知道我算的为啥不对。用数值一直除以16,得到三次余数分别是5、11、11,倒过来转换成十六进制后相加,得到的就是BB5啊。
二、八、十六进制之间的互相转换
二进制转八进制:分组
由于,每3位二进制数就可以转换成1位八进制数。所以二进制转八进制,可以采用分组转换的规则。
- 整数部分:自右向左分组,3位一组
- 小数部分:自左向右分组,3位一组
- 分组时,位数不够,用0补足。
- 最后把一组3位二进制数转换为1位八进制数,多个八进制数按序拼接
如下图,10011010110就可以从右向左三位一组,分成10、011、010、110四组。其中最左边不够三位的,用0补足成010。
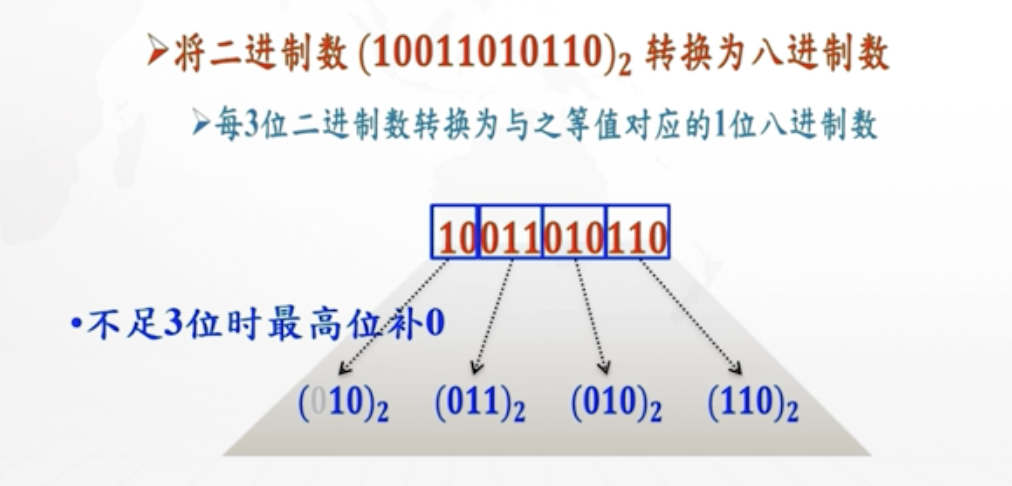
3位二进制的数,可以对应转换成0-7之间的固定数。上边分组转换后得到的八进制数分别是:2、3、2、6。
按顺序从左到右整合到一起,得到最终结果就是2326O
二进制转十六进制
同理:只不过是按四组为一位进行转换。
10011010110进行分组后得到100、1101、0110,同样的,最左边不足4位的会被0补足为0100。
4位二进制的数,其取值在0-9+A-F之间,所以,上边分组后的数据分别得到4、D、6。
按照从左到右的顺序补足后,得到4D6H
八进制转二进制:拆分
每1位八进制数转换为与之相等的3位二进制数。
如下,将2426O转成二进制数,则可以分别将2、4、2、6转为二进制数:10、100、10、110
不足三位的最高位用0补足,得到010、100、010、110
然后拼接得到最终结果:010100010110(最终结果的最高位、即最左边的0可以去掉了就)
去掉最高位0,得到:10100010110B
十六进制转二进制
同上,把每1位十六进制数,转换成4位二进制数后,高位补0再拼合即可。最终结果再去掉最高位的多余的0。
如3D6:拆分位3、D、6,
分别转成二进制:11、1101、110
不足4位的高位补零:0011、1101、0110
最后拼合:001111010110
去掉最高位的多余0,最终结果:1111010110B
八进制与十六进制相互转换
八进制不能直接按位转换成十六进制,可以借助二进制过渡。(八)->(二)->(十六)
2、8、16进制数间的关系对照表
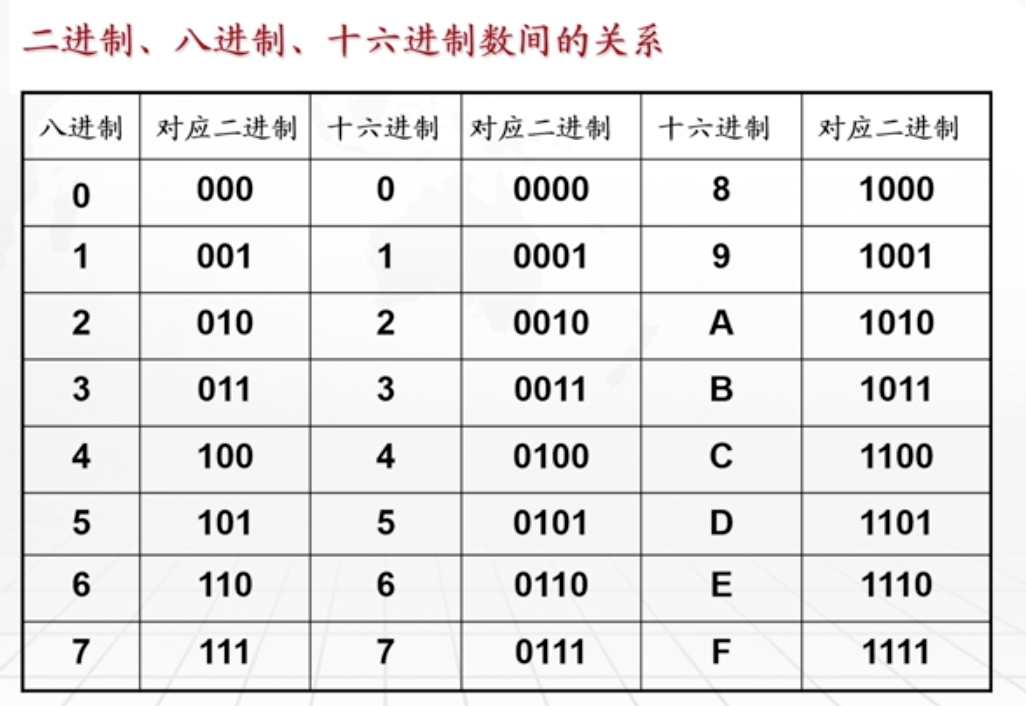
| 八进制 | 对应二进制 | 十六进制0-7 | 对应二进制 | 十六进制8-16 | 对应二进制 |
|---|---|---|---|---|---|
| 0 | 000 | 0 | 0000 | 8 | 1000 |
| 1 | 001 | 1 | 0001 | 9 | 1001 |
| 2 | 010 | 2 | 0010 | A | 1010 |
| 3 | 011 | 3 | 0011 | B | 1011 |
| 4 | 100 | 4 | 0100 | C | 1100 |
| 5 | 101 | 5 | 0101 | D | 1101 |
| 6 | 110 | 6 | 0110 | E | 1110 |
| 7 | 111 | 7 | 0111 | F | 1111 |
转换总结图:
作业:
用js封装几个函数,来进行进制转换。