Rabbits and Recurrence Relations

Wascally Wabbits

Figure 1. The growth of Fibonacci’s rabbit population for the first six months.

Figure 2. Erosion at Lake Mungo in New South Wales, which was initiated by European rabbits in the 19th Century. Courtesy Pierre Pouliquin.

In 1202, Leonardo of Pisa (commonly known as Fibonacci) considered a mathematical exercise regarding the reproduction of a population of rabbits. He made the following simplifying assumptions about the population: 1. The population begins in the first month with a pair of newborn rabbits. 1. Rabbits reach reproductive age after one month. 1. In any given month, every rabbit of reproductive age mates with another rabbit of reproductive age. 1. Exactly one month after two rabbits mate, they produce one male and one female rabbit. 1. Rabbits never die or stop reproducing.

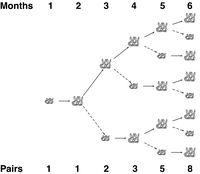
Fibonacci’s exercise was to calculate how many pairs of rabbits would remain in one year. We can see that in the second month, the first pair of rabbits reach reproductive age and mate. In the third month, another pair of rabbits is born, and we have two rabbit pairs; our first pair of rabbits mates again. In the fourth month, another pair of rabbits is born to the original pair, while the second pair reach maturity and mate (with three total pairs). The dynamics of the rabbit population are illustrated in Figure 1. After a year, the rabbit population boasts 144 pairs.
Although Fibonacci’s assumption of the rabbits’ immortality may seem a bit farfetched, his model was not unrealistic for reproduction in a predator-free environment: European rabbits were introduced to Australia in the mid 19th Century, a place with no real indigenous predators for them. Within 50 years, the rabbits had already eradicated many plant species across the continent, leading to irreversible changes in the Australian ecosystem and turning much of its grasslands into eroded, practically uninhabitable parts of the modern Outback (see Figure 2). In this problem, we will use the simple idea of counting rabbits to introduce a new computational topic, which involves building up large solutions from smaller ones. | |

解题思路

传统斐波那契数列都是生一个兔子，而此时是生 k 个兔子。

• 第 天有小兔子 个，大兔子 个，总兔子个数为 个。
• 第 天先有 个大兔子生下 个小兔子，第 天的小兔子 长得后变成大兔子，因此此时大兔子个数为 个，小兔子个数为 个，总兔子个数为 个。
• 第 天先有 个大兔子生下 个小兔子，第 天的小兔子 长得后变成大兔子，因此此时大兔子个数为 个，小兔子个数为 个，总兔子个数为 个。

因此代入公式可以轻易得到 。只要抓住上一代总共有多少，然后上一代里面大兔子有多少就 🆗！

#include <stdio.h>
int main() {
    int n, k;
    scanf("%d %d", &n, &k);
    if (n < 3) printf("1\n");
    long long int f1 = 1, f2 = 1;  // f3 = f1 * k + f2
    for (int i = 3; i <= n; i++) {
        long long int f3 = f1 * k + f2;
        f1 = f2;
        f2 = f3;
    }
    printf("%lld\n", f2);
    return 0;
}

编译运行：

b12@PC:~/ROSALIND/Rabbits_and_Recurrence_Relations$ gcc -Wall ./fibK.c -o ./fibK
b12@PC:~/ROSALIND/Rabbits_and_Recurrence_Relations$ ./fibK
35 4
48127306357829