9. 桶排序

算法描述

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效，我们需要做到这两点：

1. 在额外空间充足的情况下，尽量增大桶的数量
2. 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

对于桶中元素的排序，选择何种比较排序算法对于性能的影响至关重要。

示意

元素分布在桶中：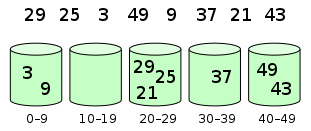

然后，元素在每个桶中排序：

算法实现

这里除了用到了桶排序之外，对桶内的元素我们使用了插入排序。
比较关键的地方是设置每个桶内容纳的元素个数，我们默认每个桶装5个元素。
知道了每个桶的容量，就可以求出在这些数值范围内有多少个桶能容纳这些元素。首先我们需要求出最大值和最小值，求出他们的差，除以每个桶的容量就可以得到一共需要多少个桶。
然后就遍历数组，求当前元素放入哪个桶中。
最后对桶中的元素进行插入排序，然后把所有桶中的元素放在一起得到最后的结果。

/**
 * 插入排序
 * @param {number[]} arr 数组
 */
const insertionSort = (arr) => {
  let current
  for (let i = 1; i < arr.length; i++) {
    current = arr[i]
    for (let j = i - 1; j >= 0; j--) {
      if (current < arr[j]) {
        arr[j + 1] = arr[j]
        if (j === 0) arr[j] = current
      } else {
        arr[j + 1] = current
        break
      }
    }
  }
  return arr
}
/**
 * 桶排序
 * @param {number[]} arr 数组
 * @param {number} bucketSize 每个桶的大小，默认为 5
 */
const bucketSort = (arr, bucketSize = 5) => {
  if (!arr.length) return arr
  let max = Math.max.apply(null, arr)
  let min = Math.min.apply(null, arr)
  const buckets = []
  const bucketCount = Math.floor((max - min) / bucketSize) + 1
  for (let i = 0; i < bucketCount; i++) {
    if (!buckets[i]) buckets[i] = []
    buckets[Math.floor((arr[i] - min) / bucketSize)].push(arr[i])
  }
  const ret = []
  for (let i = 0; i < bucketCount; i++) {
    insertionSort(buckets[i])
    ret = [...ret, ...buckets[i]]
  }
  return ret
}