6. 堆排序

算法描述

堆排序是选择排序的一种改进，将数组分成已排序和未排序的两部分，堆排序使用堆的数据结构对找到未排序部分的最大值进行了优化。

我们在这里来复习一下堆数据结构的特点：
二叉堆可以看作为一颗完全的二叉树。完全二叉树的一个性质是除了最底层之外，每一层都是满节点。所以堆可以使用数组来表示。
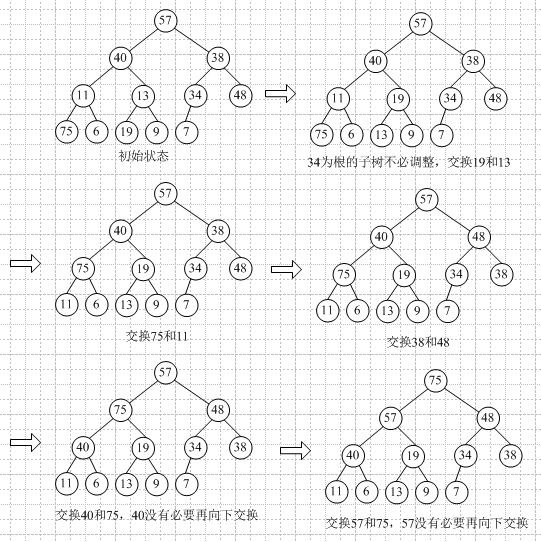
比如数组 [57, 40, 38, 11, 13, 34, 48, 75, 6, 19, 9, 7] 可以表示如下堆：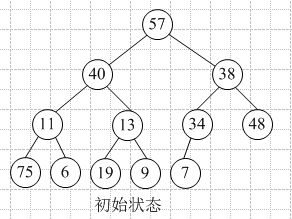

使用数组来描述堆，那么访问堆节点会有一些规律：

• 父节点 i 的左字节点元素为 i * 2 + 1
• 父节点 i 的右字节点元素为 i * 2 + 2
• 字节点 i 的父节点元素为 Math.floor((i - 1) / 2)

那么堆排序可以分成三个步骤：

1. 构建最大堆（根节点为最大值）
2. 把堆首和数组未排序的最后一个值交换
3. 把堆的尺寸缩小 1，再重新构建最大堆
4. 重复步骤 2，直到堆的尺寸为 1

遍历从下往上，从右往左

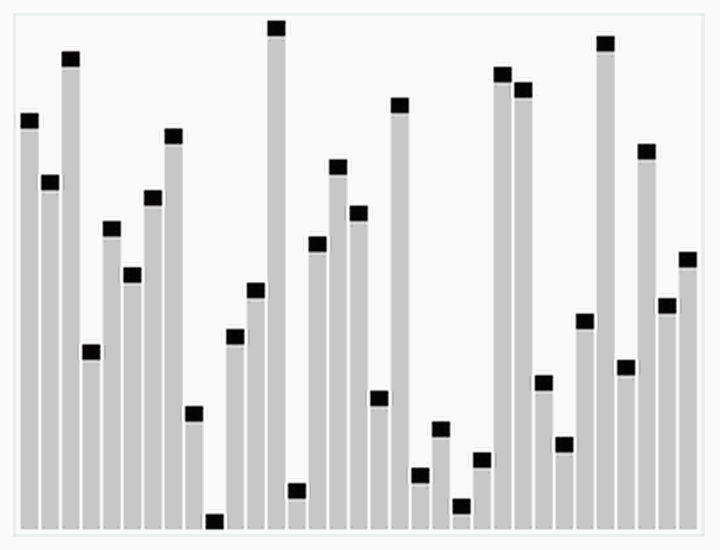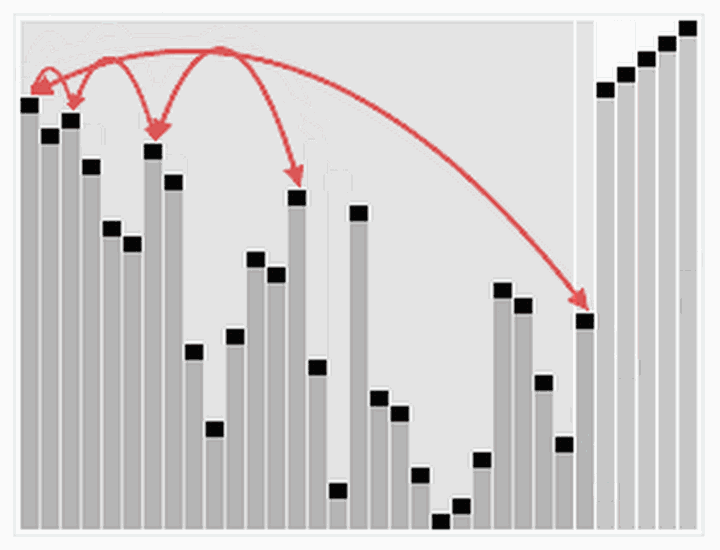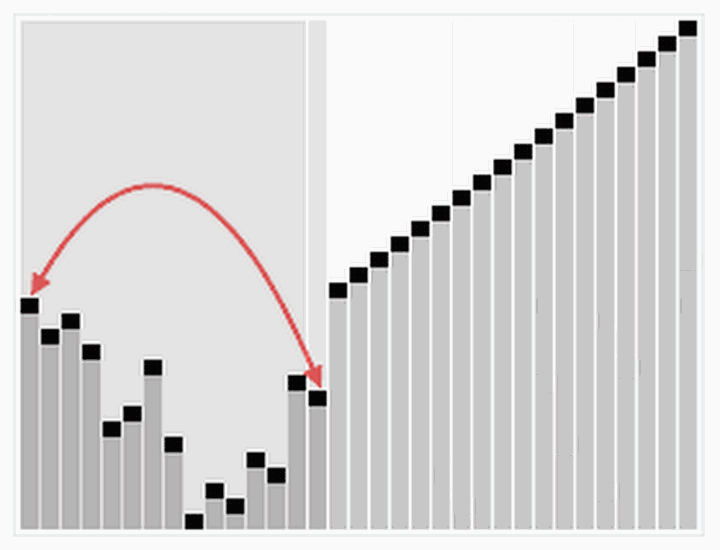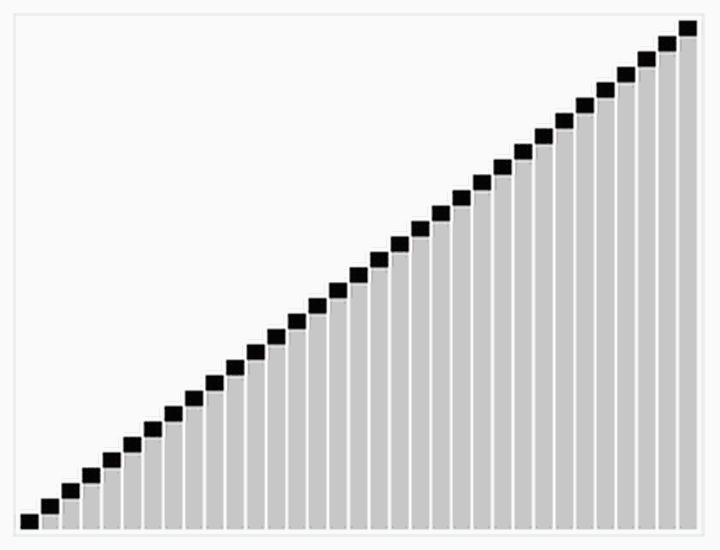
动图演示

算法实现

这里需要注意的是，构建最大堆是为了从小到大排序，构建最小堆是为了从大到小排序。

/**
 * 堆排序
 * @param {number[]} arr 数组
 */
const heapSort = (arr) => {
  // 从最后一个节点的父节点开始首先进行一次排序，父节点 i 的子节点为 2*i+1，
  // 所以最后一个节点的父节点为 Math.floor(arr / 2) - 1
  for (let i = Math.floor(arr.length / 2) - 1; i >= 0; i--) {
    maxHeapify(arr, i, arr.length)
  }
  // 因为第一次排序已经对父节点进行过堆排序了，所以之后的都对根节点
  for (let i = arr.length - 1; i > 0; i--) {
    swap(arr, 0, i)
    maxHeapify(arr, 0, i)
  }
  return arr
}
/**
 * 对 start-end 区间内的数值按照堆排序
 * @param {number} start 
 * @param {number} end 
 */
const maxHeapify = (arr, start, end) => {
  const parent = start
  let children = 2 * parent + 1
  // 如果子节点大于数组的边界，直接退出
  if (children >= end) return
  if (children + 1 < end && arr[children] < arr[children + 1]) {
    children += 1
  }
  if (arr[parent] < arr[children]) {
    swap(arr, parent, children)
    maxHeapify(arr, children, end)
  }
  return arr
}
/**
 * 交换数组中的两个元素
 * @param {number[]} arr
 * @param {number} i
 * @param {number} j 
 */
const swap = (arr, i, j) => {
  const temp = arr[i]
  arr[i] = arr[j]
  arr[j] = temp
}

堆排序的平均时间复杂度为 o(nlogn)，空间复杂度为 o(1)。