Ranking Saliency

提出了一种自底向上的图像显著区域检测方法。构造了两个具有低层和中层特征的图像流形，并开发了一种利用背景和前景查询进行排序的级联方法来生成显著性图.

这篇论文是在13年CVPR论文[Chuan Yang, Lihe Zhang, Huchuan Lu, Minghsuan Yang, Saliency Detection via Graph-Based Manifold Ranking, CVPR2013，P3166-3173]的基础上进行的扩展与改进. 实现了较高的性能提升.

仍然是利用流行排序, 通过构造图结构, 通过计算图节点与设定的查询节点(第一阶段的触及图像边缘的背景节点, 第二阶段的基于第一阶段的预测的前景节点)之间的相关性, 来以此给予对应的显著性值.

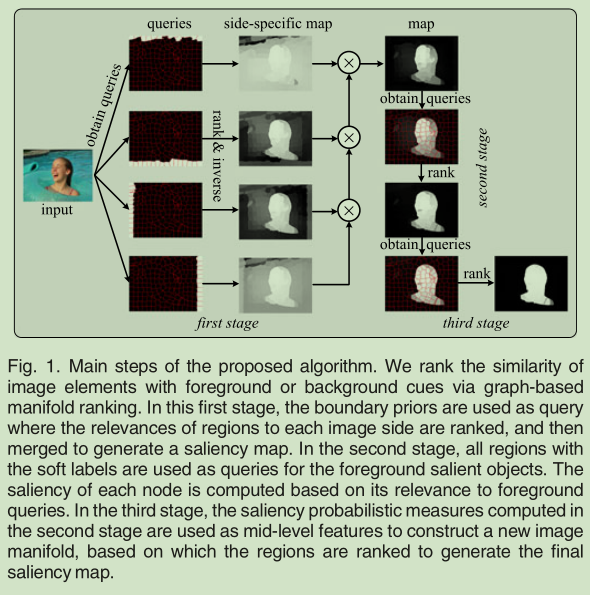
但是这篇文章, 前两阶段的大致流程类似, 多增了一个第三阶段. 在第二阶段得到的显著性图的基础上进行进一步”排序”, 这里计算权重使用的不再是前两阶段里的Lab色彩空间的距离, 而是用的是第二阶段得到的显著性图的值来计算距离(所谓利用的是中级特征). 而且这里的指示向量和第二阶段的设定是类似的. 这里需要重新计算矩阵W和D. 最终得到了最终的显著性图.

有些细节不同, 例如这里又在超像素分割的基础上, 为了检测不同尺度的显著性目标, 利用了多尺度特征. 对超像素进行聚类, 获得了三个基于区域的图结构, 对应的计算权重矩阵W和度矩阵D的过程也有了些不同. 因为要考虑到所有的四个层次尺度的节点. 而且, 对应的指示向量y也有了些许差异, 最大的差异在于第二阶段的y使用的不是01值, 用的是第一阶段得到的显著性值来作为指示.

论文内容

整体算法流程:

排序算法:

1. 将图像划分为超像素和数个区域(超像素聚类)图. 得到度矩阵和权重矩阵.
2. 计算关联矩阵A, 设定对角线元素为0.
3. 根据图像的四边设定背景指示向量获得四个对应的显著性图并进行集成. 获得第一阶段的输出.
4. 根据第一阶段输出设定新的前景指示向量. 计算显著性图. 为第二阶段的输出.
5. 使用得到的显著性图得到新的权重矩阵W和度矩阵D. 计算关联矩阵A, 设定对角元素为0.
6. 同时根据得到的显著性图获得新的指示向量. 计算新的相关性值, 获得最终的显著性图.

构建图结构

基于图的流形排序是学习最优关联矩阵的关键[T. Kim, K. Lee, and S. Lee, “Learning full pairwise affinities for spectral segmentation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2010, pp. 2101–2108.]，充分捕捉了图的内在结构信息，描述了图标记任务的局部和全局分组线索。

基本设定与[Chuan Yang, Lihe Zhang, Huchuan Lu, Minghsuan Yang, Saliency Detection via Graph-Based Manifold Ranking, CVPR2013，P3166-3173]没什么区别.

以及要使用的最终解:

以及进一步的优化表示:

开始构建多尺度图结构, 先使用SLIC算法划分超像素, 进行如下算法流程:

由于在一个场景中，多个感知不均匀的区域可能以不同的尺度出现显著的物体，因此我们考虑使用多尺度图对图像空间进行多重量化。

也就是在超像素图结构的基础上, 使用 K-way 分割算法进行分组操作(group), 使用形成的区域作为新的图层节点. 最终的结果是四个图. 一个超像素为节点, 另三个为区域为节点.

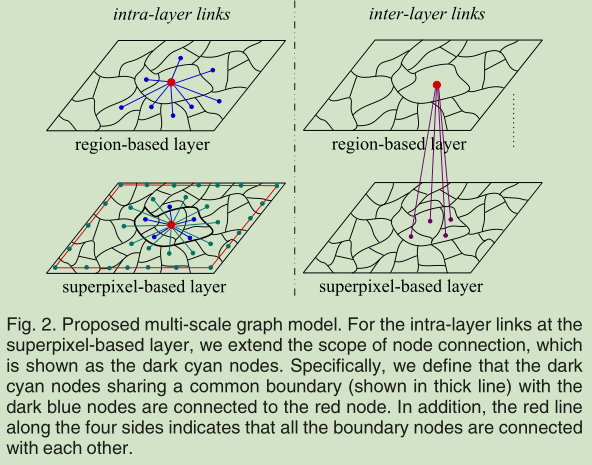
对于节点的邻接关系(边连接的问题), 有如下设定(可对照上图):

1. 对于三个区域层与超像素层之间的关系:
   1. 对于基于区域的层, 不同区域之间不存在边. 只连接区域内部的超像素
   2. 区域层之间不考虑连接
   3. 这里只是设定了区域层与超像素层之间
2. 对于层内节点的关系:
   1. 基于区域的层, 存在共享边界的区域存在边连接, 对于基于超像素的层
   2. 每个节点连接到了它相邻的和与其邻居存在共享边界的节点(两圈)
3. 对于边界上的超像素节点(谈到超像素, 那就是只有那一层):
   1. 任意两个都认为是互相邻接的

三个阶段

下面的三个阶段主要基于公式:

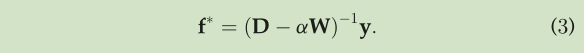
第一阶段: 使用背景查询排序

W, D	y
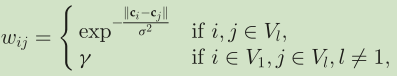	yi=1: 对应的节点i是背景查询; yi=0: 对应的节点i是未标记数据
c: 对应的超像素/区域节点对应于CIELab色彩空间的平局颜色 σ: 控制层内权重的关联尺度 γ: 是一个决定层间权重的约束	指示向量的长度应该是所有的四层节点的数量.

从上面的权重项的表达式可以看出来:

1. 相较于13CVPR的那篇论文, 这里多了一个层次的设定, 这里的权重也就要考虑层次之间的问题, 要注意, 这里层间的权重有些特别, 只包含区域层与超像素层之间的关系, 没有区域层之间的关系, 可以看出来, 前面的连接设定没有区域层之间的.
2. 这里整体来看, 实际上认为有效的连接, 是指的被重新分组的超像素和对应得到的包含其的区域之间, 以及相邻的聚类, 相邻的超像素以及与邻居相邻的超像素之间, 以及边界节点之间的连接. 不过这里最终计算是使用四个图一起计算得到超像素图上的权重分布. 所以后面的计算, 是直接看超像素图的权重就可以了.
3. 这里的wij的理解:
   1. 两个不同层之间的节点的连接, 最终在得到的W矩阵上, 如何反映? W矩阵应该是m(第一层的节点数所有的节点数)xn(所有图层的节点数), 从所有图层的节点映射到第一层(那些无关的节点直接权重不用管, 实际计算的时候, 还会使用邻接矩阵与w相乘, 来计算对应的有效的权重, 这个矩阵有很多不是邻接(不是有效的连接)的节点的权重是要被置为零的).

具体的流程与之前的论文相同, 使用分离组合的策略计算四个边界对应的显著性图集成的最终结果.

使用这一侧的超像素节点作为背景查询，其他节点作为未标记的数据.

最终集成四个显著性图的时候,

这里最终使用的是相乘运算. 这里考虑了四种集成的运算, 测试中, 乘法效果更好一些. 要是在深度网络中, 还可以使用拼接的方式. 除了这些, 就没有方法了么?

第二阶段: 使用前景查询排序

W, D	y
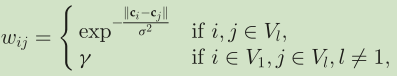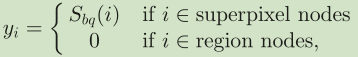c: 对应的超像素/区域节点对应于CIELab色彩空间的平局颜色 σ: 控制层内权重的关联尺度 γ: 是一个决定层间权重的约束	指示向量的长度应该是所有的四层节点的数量.
	注意: 这里的指示向量不再是0, 1值, 变成了第一阶段预测的显著性结果, 不再进行二值化. 而且这里只计算超像素节点, 不再考虑区域节点.

使用下式获得最终的第二阶段的结果.

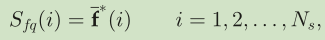
第三阶段: 使用中级特征重排序

第三阶段使用第二阶段的输出作为中级特征来构建新的图. 这里节点连接关系, 仍然和前两个阶段的设定一致.

W, D	y
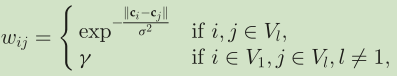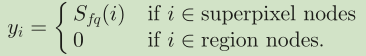c: 对应的超像素/区域节点在第二阶段输出显著性图Sfq值, 而不再是CIELab色彩空间值了. σ: 控制层内权重的关联尺度 γ: 是一个决定层间权重的约束	指示向量的长度应该是所有的四层节点的数量.
	注意: 这里的指示向量不再是0, 1值, 变成了第二阶段预测的显著性结果, 不再进行二值化. 而且这里只计算超像素节点, 不再考虑区域节点.

在排序中使用中级特性可以更好地描述图节点的关联，并进一步扩大 目标与目标节点之间的平均相关性 与 目标与背景/背景与背景之间的平均相关性 的距离.

最终得到了最后的显著性结果.

实验分析

参数设定

中级特征的效果

a: 可以看出，对象内部的关联值远大于对象与背景/背景内部的关联值 c: 中级特征得到的相关性更强, 汇聚能力更强. 所以一定程度上可以认为使用中级特征对于显著性的高亮是有益的. d: 为了验证能够均匀高亮显著性区域, 这里比较了中级低级特征对应的方差情况, 中级特征计算的结果是更小的. 这里应该是和真值计算比较.

结构自身的一个细致评估

a: 使用为标准化拉普拉斯矩阵效果更优 b: 使用k-正则图的闭环约束效果最优 c: 使用SC流程效果好于整体边界计算 d: 对A设置对角线元素为0效果更好 e: γ参数值的测试, 可见并不敏感

测试结构的各个阶段造成的性能提升

测试各种特征的效果

我们使用LBP、HOG和DRFI特征来表示图节点。

DRFI特征由区域对比度和背景线索组成，用于学习显著目标检测的回归量(regressor)[68]

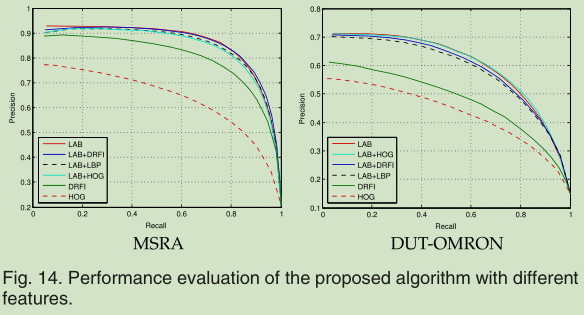
如图14:

1. 在我们的算法上, 采用LAB+DRFI或LAB+ HOG, 与使用LAB特征, 性能相当(在MSRA&DUT-OMRON).
2. 另一方面，当我们的算法使用DRFI或HOG特征时表现不佳.
3. 这些结果表明，颜色线索在两个数据集的显著性检测中发挥着更重要的作用.

一些知识

1. 人脸对于自下而上的方法来说, 可能并不突出, 相较于复杂环境中的其他显著性目标而言. 但是人累的观察却可能会注意存在人脸的区域. M. Cerf, J. Harel, W. Einhauser, and C. Koch, “Predicting human gaze using low-level saliency combined with face detection,”in Proc. Adv. Neural Inf. Process. Syst., 2007, pp. 241–248.
2. 由于突出的对象通常是紧凑的”东西”(如人或车)，而不是”物质”(如草或天空)，因此它们很少占据图像的三个或所有的边，因此所提出的SC方法确保至少两个显著性地图是有效的.
3. 基于图的流形排序是学习最优关联矩阵的关键[T. Kim, K. Lee, and S. Lee, “Learning full pairwise affinities for spectral segmentation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., 2010, pp. 2101–2108.]，充分捕捉了图的内在结构信息，描述了图标记任务的局部和全局分组线索.
4. 对于图标记的方法, 主要的一个问题是, 对于选择的种子/查询很敏感.
5. 图结构可以使用关联测度和潜在的几何结构来表达图像元素之间的关系.

参考资料

The ranking algorithm [50] is derived from the work on semi-supervised learning for classification [54]. Essentially, manifold ranking can be viewed as an one-class classification problem [55], where only positive examples or negative examples are required. We obtain a ranking function using the unnormalized Laplacian matrix [51] in (2)…

• 50: D. Zhou, J. Weston, A. Gretton, O. Bousquet, and B. Scholkopf, “Ranking on data manifolds,” in Proc. Adv. Neural Inf. Process. Syst., 2004, pp. 1–8.
• 54: Learning with Local and Global Consistency PPT: https://pdfs.semanticscholar.org/1a55/01b537d94178c723ee475a59e3345e9e89c8.pdf
• 51: F.-R. Chung, Spectral Graph Theory. Providence, RI, USA: Amer. Math. Soc., 1997.
• 55: B. Scholkopf, J. Platt, J. Shawe-Taylor, A. Smola, and R. Williamson, “Estimating the support of a high-dimensional distribution,” Neural Comput., vol. 13, pp. 1443–1471, 2001.