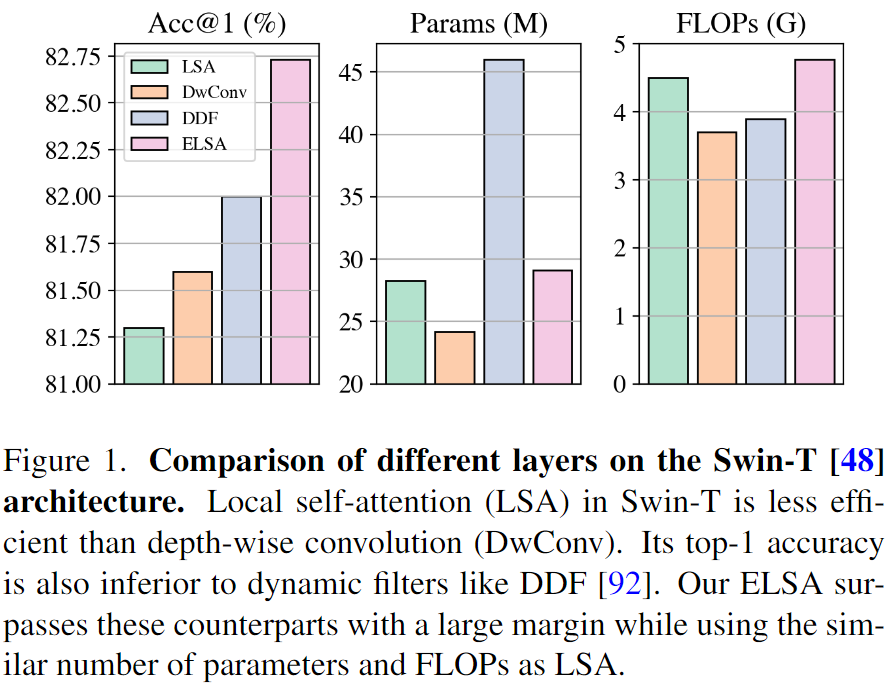
image.png
image.pngimage.png
这篇论文的思路非常有意思，主要探究了局部自注意力相对于深度分离卷积和动态卷积在性能上存在差异的主要原因。为了探究主要的差异，这篇文章两大方面入手分析。

通道设定

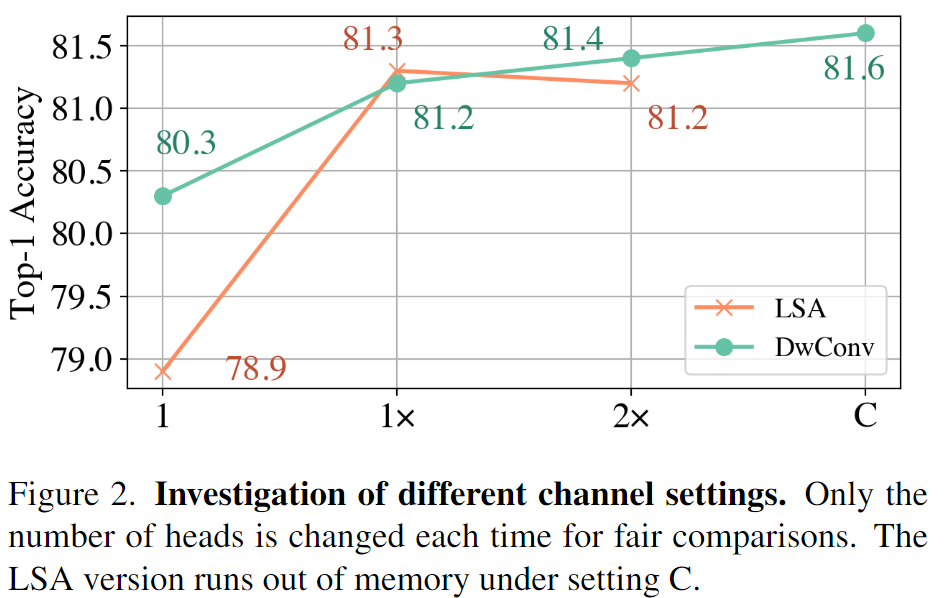
image.png

  • 这部分主要和深度分离卷积比较，因为有些文章中也展示出了，深度分离卷积可以实现和局部自注意力相当的效果。而自注意力和深度分离卷积的一个明显的差别就在于通道的设置上。
    • LSA adopts the multi-head strategy, which shares filters (a.k.a attention maps) within each group of channels.
    • In this work, we consider the channel setting of DwConv as a special case of the multi-head strategy, where the number of heads is set to the number of channels.

  • 实验结果显示，即使使用相同数量的头，深度分离卷积仍然可以实现相似或者更好的效果。所以可见通道不设置是主要的影响因素。

    空间设定

    How to obtain and apply filters (or at-tention maps) to gather spatial information is another dif-ference between DwConv, dynamic filters, and LSA.

  • DwConv shares static filters across all feature pixels in a sliding window way.

  • Dynamic filters [39, 42, 66, 83, 92] employ a bypath network, normally a 1x1 convolution, to generate spatial-specific filters, and apply these filters to the neighboring area of each pixel. (这里主要讨论空间不共享的滤波器，而非CondConv这种仅是最终核形式与输入相关的普通卷积)
  • LSA generates attention maps, which are also a kind of spatial-specific filters, via the dot product of the query and key matrices. LSA applies these attention maps to local windows.

针对空间设定部分，作者们为了便于分析，首先将三种空间操作的形式进行了统一。

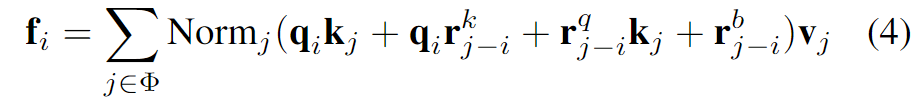
| image.png
统一形式
- Normj can be either the identity mapping, the filter normalization, or softmax.
- rkj-i and rqj-i are relative position embeddings.
- rbj-i denotes the relative position bias.


The spatial processing of LSA and its counterparts are essentially different in three factors:
- parameterization,
- normalization,
- filter application.

这一形式类似于https://spaces.ac.cn/archives/8130#DeBERTa%E5%BC%8F中所提到的DeBERTa式的编码结构。 | 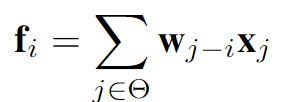image.png
标准卷积、深度分离卷积
这里的权重w可以看做是统一形式中的相对位置偏置
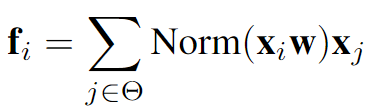
relative position bias | | —- | —- | | | image.png
动态卷积
这里的权重计算过程可以看做是统一形式中的相对位置嵌入
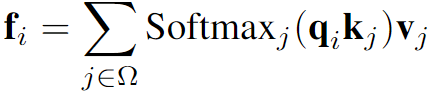
relative position embedding | | | image.png
（局部）自注意力 |

从而进一步从以下三个角度进行了分析。

参数化策略

image.png

  • A variant of dynamic filters (Net6) is on par with the LSA in Swin-T.

  • Moreover, Net7 indicates that combining the parameterization of LSA with dynamic filters can further boost the performance, when applying filters to local windows.

    归一化策略

    image.png
    Normalization is another factor that influences spatial processing.

  • DwConv and Involution adopt identity mapping as normalization.

  • DDF introduces the filter normalization.
  • LSA and Outlooker employ the softmax function as normalization.

This indicates that the normalization part should not be blamed for the mediocre performance of LSA.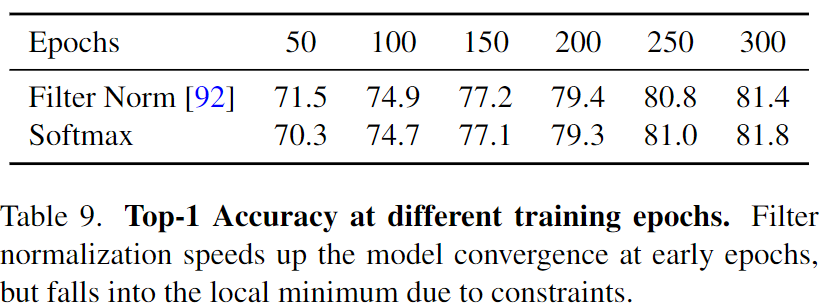
image.png
As can be seen, the Filter Normalization can speed up model convergence at early epochs. However, due to the constraint of 0 mean and 1 variance in Filter Normalization, the flexibility of filters are limited. Therefore, in the last 100 epochs, Net7 with Filter Normalization lags behind the softmax version.

滤波器应用形式

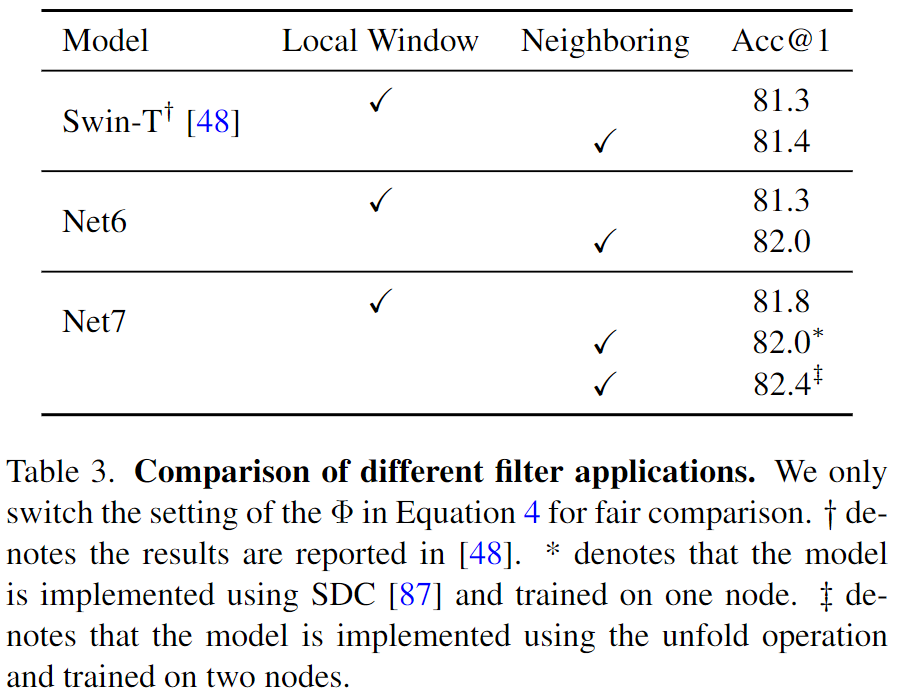
image.png

  • LSA in Swin Transformer applies attention maps to non-overlapping local windows.
  • In contrast, DwConv and dynamic filters apply filters to sliding neighboring areas.

When applying filters to neighboring areas, both Net6 and Net7 get significantly improved, indicating that the neighboring application is critical for spatial processing.

核心结论

The reason why DwConv can match the performance of LSA is because of the neighboring filter application. Without that, DwConv degenerates to a variant of Net4, which is inferior to LSA.
Similarly, the reason why dynamic filters perform better than LSA is because of the relative position em-bedding and the neighboring filter application. Integrating these factors into LSA (Net7-N) achieves the best perfor-mance among all these variants.
The peak performance of the local window version is worse than the neighboring one. Another disadvantage of the local window is that it requires strategies like window shifting to exchange information between windows, which limits the model design to have pairs of layers at each stage. 如果使用了滑动窗口，其实就减弱了需要引入额外的窗口交互的必要性。

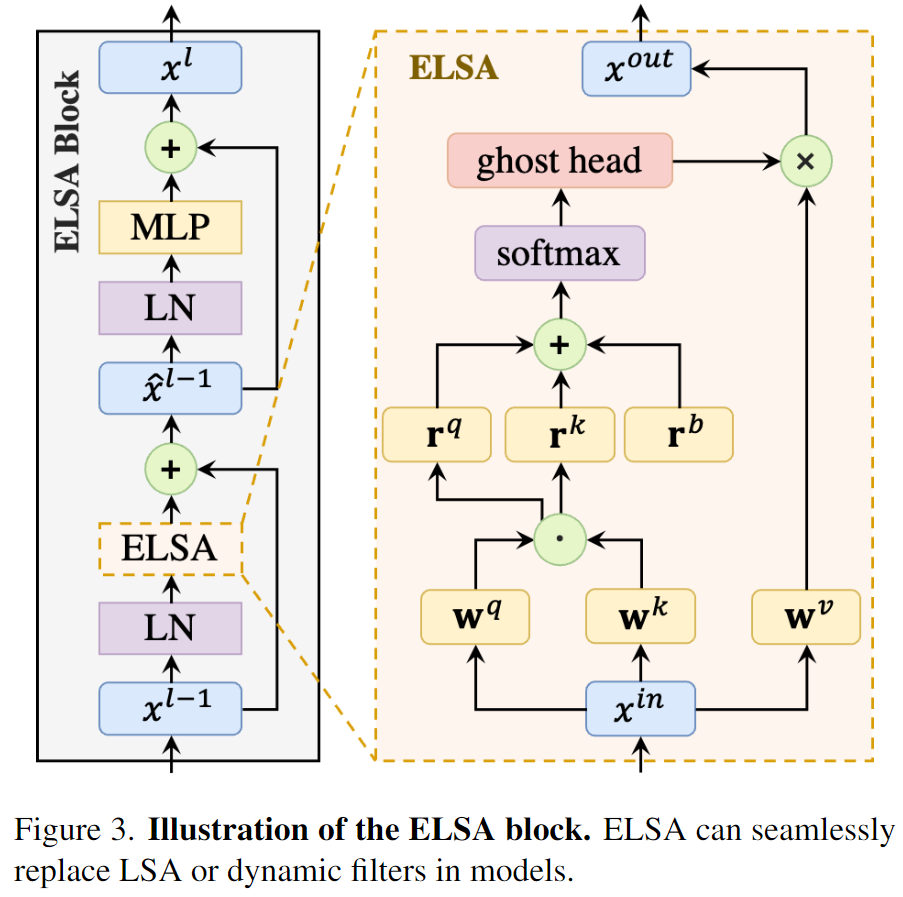
对局部自注意力机制的改进——Enhanced Local Self-Attention

考虑到以上的分析，作者们设计了一种改进版本的局部自注意力机制：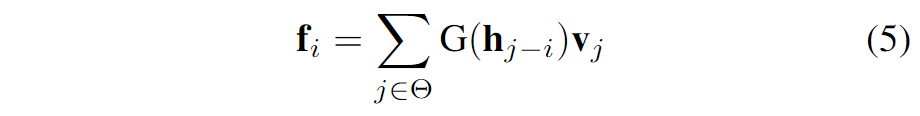
image.png
核心在于局部划窗形式的增强和多头扩展的容量提升的设计。这里的h是the Hadamard attention value，而G是the ghost head mapping。

Hadamard attention

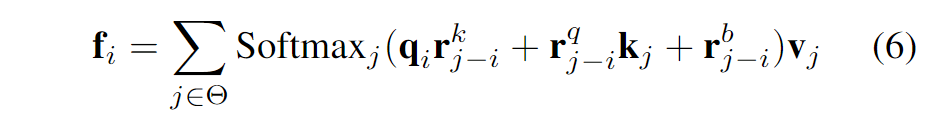
image.png
由于原始的形式4中涉及到矩阵的乘法操作，会引入大量的计算成本，这里就将其进行删除，也就变成了表3中的Net6。作者分析，其性能弱于Net7可能是因为其注意力计算过程中包含着qk这样一个二阶的项，从而整体Net7是一个三次映射，而Net6仅是一个二次映射。One common hypothesis in deep learning is that the mappings with the higher order have stronger fitting ability [A Non-convex One-Pass Framework for Generalized Factorization Machine and Rank-One Matrix Sensing]. 为此，作者希望设计一个模块可以维持三阶映射，但是又不希望由此引入矩阵乘法带来的太多的计算成本。为此，作者们设计了Hadamard attention，通过使用q和k之间的Hadamard product来作为一个二阶项，同时又不会带来计算负担。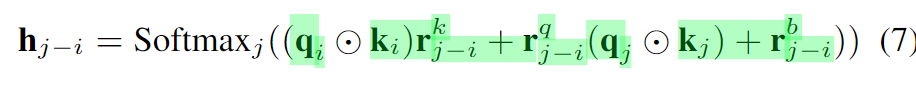
image.png

Ghost Head

在前面的实验中，更多的头会带来更好的通道容量，也会促使DeConv版本的模型获得更好的表现。而直接增大LSA的头数量却并不会带来增益。为此设计了Ghost Head结构来提升容量的同时也获得更好的性能。这里的设计思路受到GhostNet的启发，引入了两个静态矩阵：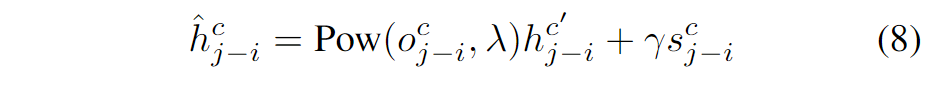
image.png
这里直接解释的话并不直观，可以看伪代码：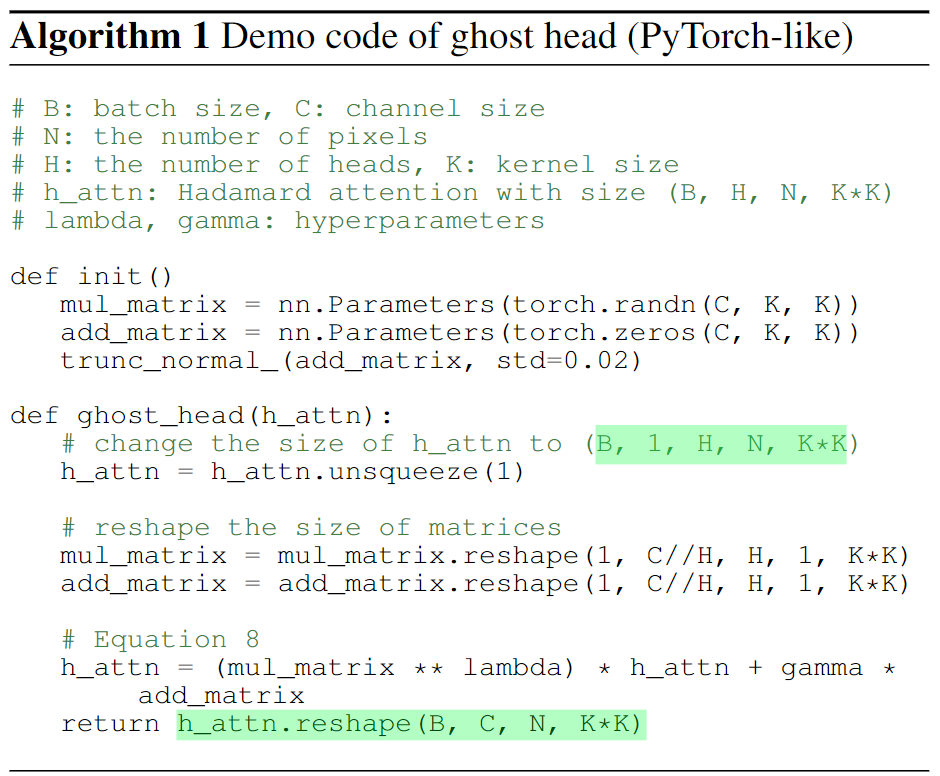
image.png
通过这一模块实现了多个头的扩展。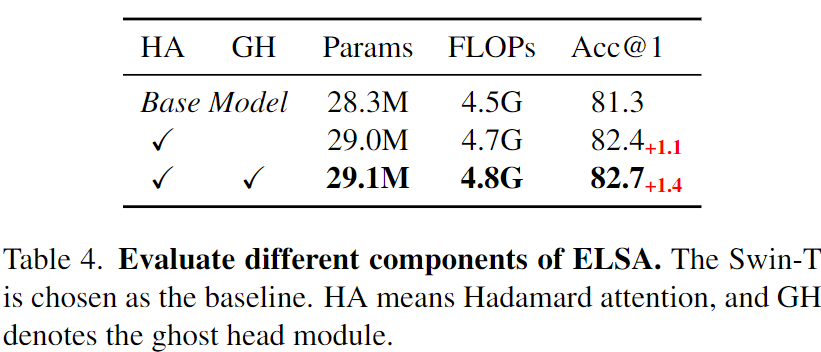
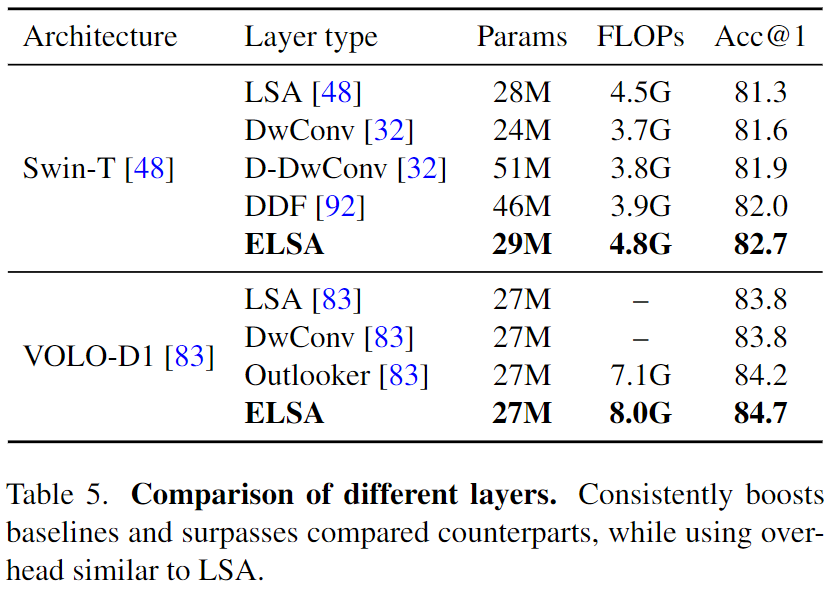
image.pngimage.png
Ghost也可以用到全局注意力上。
We apply the ghost head module to global self-attention maps after softmax. Instead of expanding the number of heads to the number of channels, in the global self-attention case, the ghost head module only doubles the number of heads.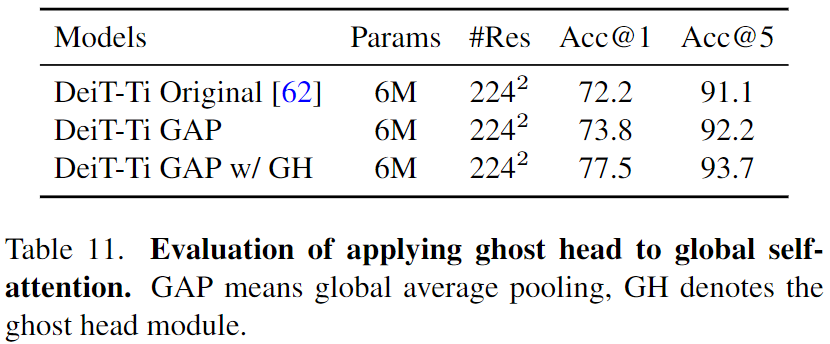
image.png

实现上的关键

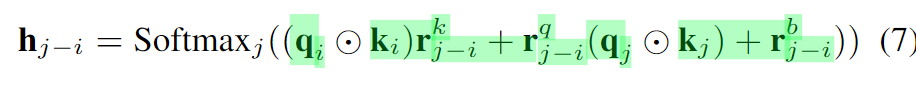
image.png
考虑到这里仍然设计到局部划窗的计算，实现起来其实并不容易。作者给出了三种渐进式的改写：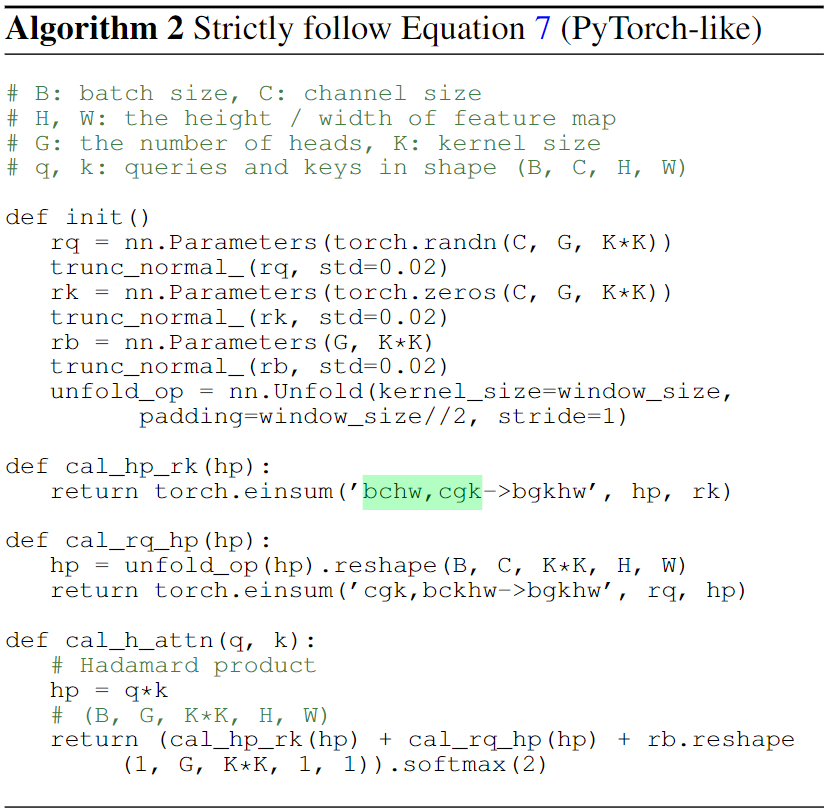
image.pngimage.png
二者结果其实是一样的：

  1. import torch
  2. import torch.nn as nn
  3. import torch.nn.functional as F
  5. C = 2
  6. K = 3
  7. H = 4
  8. W = 4
  9. G = 3
  10. B = 1
  12. tensor = torch.randn(B, C, H, W)
  13. rq = torch.randn(G, K * K, C)
  15. # unfold
  16. # 这里c为输入通道，k组卷积核，每一组内包含g个，但是每一组仅仅作用于K*K内的一点。
  17. # 这样对应的卷积操作相当于是将输入和输出分成k组来进行分组卷积，而这组内的输入来自局部邻域的各个位置。
  18. # 整体是相当于对这K*K内各个点使用独立的gxcx1x1计算了，而这一计算对于bxhxw这些点都是一样的。
  19. # 不同于标准的卷积操作，其核心是整个局部邻域内的聚合计算，而无法实现针对局部邻域的非共享的单一变换。
  20. # 从整体来看，这一操作就是全局共享，局部非共享的点操作。也可以看做是空间局部独立的1x1卷积
  21. unfold_ops = nn.Unfold(kernel_size=K, padding=1, stride=1)
  22. hp = unfold_ops(tensor).reshape(B, C, K * K, H, W)
  23. unfold_rq_hp = torch.einsum("gkc, bckhw -> bgkhw", rq, hp)
  25. # dwconv
  26. # 前面操作的目的就是全局共享，局部非共享。
  27. # 考虑到1x1卷积具有全局共享，通道独立，以及点操作的特性，接下来就是该思考，如何为其引入额外的局部非共享的设计。
  28. # 这里的设计就是借助于通道维度来间接实现空间局部的权重独立。
  29. # 由于每个卷积核对应的输入都是一样的，所以对于独立的点空间的计算，可以转化为独立的1x1卷积核针对整个空间的共享计算。
  30. # 也就是将这些空间局部独立的卷积核堆叠到通道维度上。从而构成了（G * K * K, C, 1, 1）大小的卷积核。
  31. # 但是直接堆叠卷积核计算后，这些空间上的变换被整体堆叠到了通道维度上，成了(B,GKK,H,W)。
  32. # 为了获得与局部空间映射等价的结果，这里需要对通道进行空间偏移。
  33. # 也就是说，只有偏移后，这些堆叠在同一位置的通道上的特征才是来自局部空间各个位置上的特征，这样才能通过形变恢复合理的(G,K*K,H,W)的形状
  34. # 即每个空间（H,W）上的一点实际上对应着一个以其为中心的局部邻域的特征（K*K,H,W）。
  35. rq_hp = F.conv2d(input=tensor, weight=rq.reshape(G * K * K, C, 1, 1), padding=0, stride=1)
  36. kernel = torch.zeros(G * K * K, 1, K, K)
  37. for i in range(G * K * K):
  38.     _id = i % (K * K)
  39.     # 对于每个输出的卷积核通道内部的元素而言，对应的c个输入权重是一致的（因为是1x1卷积）
  40.     # 所以通过空间偏移来计算的时候，得到的结果和先偏移再计算加权聚合的结果也是一致的。
  41.     # 通过这样的偏移实现了对于输入特征局部区域位置上区域到区域的映射，而非聚合为1点（当然，这些结果加起来的时候就类似于区域卷积了）。
  42.     _x = _id % K
  43.     _y = _id // K
  44.     kernel[i, 0, _y, _x] = 1
  45. dwconv_rq_hp = F.conv2d(input=rq_hp, weight=kernel, padding=K // 2, groups=G * K * K).reshape(B, G, K * K, H, W)
  46. print(torch.all(torch.isclose(unfold_rq_hp, dwconv_rq_hp)))

另外作者还提供了一种对算法3的简化版
image.png
即将两个独立的卷积合并到了一起。
具体实现中，作者使用的是CUDA版本的自定义算子。这个应该仔细学习下。

链接