图片.png

使用贝叶斯公式来计算了最终的显著性图(实际上就是后验概率).

首先利用Harris Point生成一个粗定位目标的凸包, 有效的利用角点所构建出来的凸包区域来计算大致的显著性区域。
其次，基于超像素将凸包区域聚类为两个内聚类; 然后根据颜色的不同从内部聚类中选择显著性聚类，建立先验图，并计算凸包的观测似然。最后利用贝叶斯框架对像素p的先验映射和观测似然进行整合.

  • 先验概率, 先对凸包内外超像素进行聚类, 进而利用簇之间的色彩距离, 确定显著性簇, 对于所有的超像素, 利用超像素间的色彩和空间距离的倒数来计算显著性值, 对其归一化, 作为这里的先验概率.
  • 条件概率, 使用的是像素的CIELab色彩空间的三个色彩特征统计直方图中的三个对应于原像素所在块(bin)的像素占整体区域像素比例的累乘获得.

论文解析

转自参考链接所指文章.

文章主要利用贝叶斯推导模型来得到显著性检测映射图。贝叶斯推导模型的计算公式如下图：

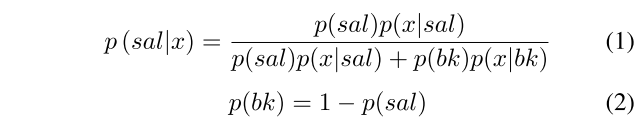
图片.png

后验概率的意义是，在已知当前像素点的条件下，当前像素点为显著性目标的概率。

为了构建贝叶斯概率模型，需要提前计算出显著性值以及得到显著性区域。

文中利用color boost方法来计算角点检测，有效的利用角点所构建出来的凸包区域来计算大致的显著性区域。由于凸包能够很好的将图像区域分割为两个部分，也就大致得到了显著性区域以及背景区域。在得到大致的显著性范围以及背景范围之后可以很有效的利用统计直方图来计算每一个像素的条件概率。计算公式如下图所示：

image.png

其中N表示在显著性区域(凸包内区域, 更可能是显著性区域)S或者背景区域(凸包外区域, 更可能是背景)B中存在的像素的个数，而S()以及B()则表示对应的区域(S or B)内色彩统计直方图中和该像素特征相对的条形(指的是直方图上的条形)的值(也就是对应的相同特征像素数量)。

也即是说, S(f(x))表示的是显著性区域内, 颜色特征相同的像素数量, 这个比值计算的是已知显著性的像素的前提下, 对应的色彩空间相同的像素比例. 实际上:

  • S()与B()就类似与一个将像素点的特征映射到直方图上的一个函数, 对应的值就是直方图上的取值(相同特征的像素数量).
  • S(f(x))表示从前景像素中, 查找对应于f(x)这个特征值的像素数量.
  • /Ns, 则是计算这部分像素在前景像素中占的比例
  • 也就是说, 7式是在表示研究的像素x和前景区域的相似程度, 同理, 8表示, 研究的像素和背景区域的相似程度. 因为越相似, 对应的分子的值越大(表示这个特征在这个区域里占主要地位).
  • 三个颜色通道的结果的乘积(认为是独立的), 就得到了似然函数.

经过上面的处理，就得到了每个像素点的观察概率。

为了更进一步计算每一个像素点的显著性，需要得到一个更为精细的显著性目标区域，为了在这个现有的显著性目标凸包范围内进一步提纯，利用已有的信息进行对比度计算。

首先，利用聚类算法将凸包内的显著性区域和凸包外面的背景区域进行聚类处理，以防止区域内的显著性噪声。聚类之后，以每一个聚类为单位进行凸包内和凸包外的超像素之间的距离计算。

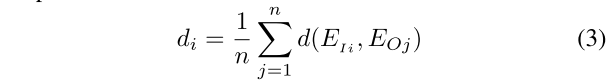
图片.png

文中选择距离最大的凸包内的超像素块作为显著性目标，并利用得到的这一信息进一步得到每一个超像素块的显著性数值。利用其它超像素块到显著性目标聚类内的超像素块之间的对比度就可以有效的计算每一个超像素块k的显著性数值。

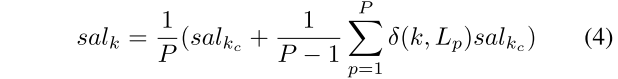
图片.png

关于其中的第二项, 由于位于显著性聚类内部的超像素块中，当k等于Lp的时候，不被计算，所以累加的次数等于P-1次。为了弥补这样的不平衡，当超像素位于显著性聚类内部时，利用显著性聚类内部的显著性平均值作为其自身的显著性值。

因此，计算每一个超像素的显著性数值公式如下：

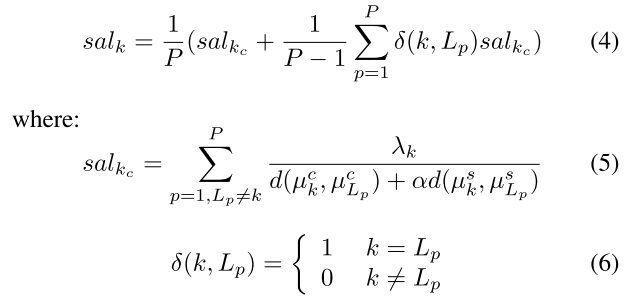
图片.png

K个超像素, 聚类后, 每个聚类内部有P个超像素. 显著性目标聚类中第p个超像素表示为Lp.

这里计算的是所有超像素的显著性值. 只不过Lp指代的是显著性目标聚类中的超像素.

选择距离最大的凸包内的超像素块作为显著性目标，并利用得到的这一信息进一步得到每一个超像素块的显著性数值。

利用 所有的其它超像素块到显著性目标聚类内的超像素块之间 的对比度就可以有效的计算每一个超像素块k的显著性数值.

由于位于显著性聚类内部的超像素块中，当k等于Lp的时候，不被计算，所以累加的次数等于P-1次。 为了弥补这样的不平衡，当超像素块位于显著性聚类内部时，利用显著性聚类内部的显著性平均值作为其自身的显著性值, 也就是第二项. 式子中与p已经无关, 本身就是P-1项的加和, 并没有计算k=Lp处的值, 所以取了其他位置的结果的平均作为自己的显著性值. 总体算了一个平均(也就是1/P).

对于外部的超像素, 第二项也就不存在了.

利用该公式就可以得到每一个超像素的显著性数值，将其放入到贝叶斯推导模型中就能够有效的计算出最终的显著性检测结果。

参考链接