- 169. 多数元素(众数与投票算法)">169. 多数元素(众数与投票算法)
- 公倍数与共因数
- 204. 计数质数">204. 计数质数
- 762. 二进制表示中质数个计算置位">762. 二进制表示中质数个计算置位
- 504. 七进制数(标准进制转换)">504. 七进制数(标准进制转换)
- 168. Excel表列名称(进制转换变种)">168. Excel表列名称(进制转换变种)
- 171. Excel 表列序号(上面一题的逆推)">171. Excel 表列序号(上面一题的逆推)
- 415. 字符串相加">415. 字符串相加
- 67. 二进制求和(字符串加法的变形题)">67. 二进制求和(字符串加法的变形题)
- 326. 3 的幂(求n是否为3的幂次方)">326. 3 的幂(求n是否为3的幂次方)
- 1109.航班预定统计(差分数组)
- 165.比较版本号(简单的进位处理)
- 随机与取样
- 384. 打乱数组(关键在于如何保存原数组)">384. 打乱数组(关键在于如何保存原数组)
- 528. 按权重随机选择(前缀和来写)">528. 按权重随机选择(前缀和来写)
- 382. 链表随机节点(水库算法)">382. 链表随机节点(水库算法)
- 470. 用 Rand7() 实现 Rand10()(随机生成随机)">470. 用 Rand7() 实现 Rand10()(随机生成随机)
- 398. 随机数索引(水塘抽样)">398. 随机数索引(水塘抽样)
- 478. 在圆内随机生成点">478. 在圆内随机生成点
- 剑指 Offer II 071. 按权重生成随机数(二分法+前缀和)">剑指 Offer II 071. 按权重生成随机数(二分法+前缀和)
- 循环
- 238. 除自身以外数组的乘积(可以看)">238. 除自身以外数组的乘积(可以看)
- 462. 最少移动次数使数组元素相等 II(数学的魅力)">462. 最少移动次数使数组元素相等 II(数学的魅力)
- 492. 构造矩形(简单)">492. 构造矩形(简单)
- 202. 快乐数(快慢指针)">202. 快乐数(快慢指针)
- 31. 下一个排列">31. 下一个排列
- 算法
- 780. 到达终点(倒序)">780. 到达终点(倒序)
- 357. 统计各位数字都不同的数字个数(排列组合)">357. 统计各位数字都不同的数字个数(排列组合)
- 479. 最大回文数乘积">479. 最大回文数乘积
- 1037. 有效的回旋镖(判断三点是否共线)">1037. 有效的回旋镖(判断三点是否共线)
- 数组
169. 多数元素(众数与投票算法)
众数
因为多数元素大于n/2,所以排序之后数组中间的数一定是众数
class Solution {public int majorityElement(int[] nums) {Arrays.sort(nums);return nums[nums.length / 2];}}
投票算法
class Solution {public:int majorityElement(vector<int>& nums) {int candidate = -1;int count = 0;for (int num : nums) {if (num == candidate)++count;else if (--count < 0) {candidate = num;count = 1;}}return candidate;}};
公倍数与共因数
利用辗转相除法,我们可以很方便的求得两个数的最大共因数;将两个数相乘再除以最大共因数即可得到最小公倍数。
//计算最大公因数int gcd(int a, int b){return b == 0? gcd(b, a%b);}//计算最小公倍数int lcm(int a, int b){return a*b/gcd(a, b);}
204. 计数质数
实现方法就是最外层遍历所有数,遍历当当前数时,将所有小于n并且是当前数倍数的数都置为false;记录所有为true的情况。
class Solution {public:int countPrimes(int n) {int res = 0;//返回值vector<bool> arry(n, true);//记录后面的元素是否为质数for(int i = 2; i < n; i++){//从2开始是因为0和1的倍数存在影像,且都不为质数。if(arry[i]){res++;for(int j = i*2; j < n; j = j+i){arry[j] = false;}}}return res;}};
762. 二进制表示中质数个计算置位
判断数是不是质数,可以枚举,从2开始枚举相除,如果余数为0就不是指数
- 这里为什么不使用上面的计数指数的方法呢,是因为这里的是没有规律的,使用暴力解法更加简洁
- 这里使用__builtin_popcount,或者使用x&x-1,能够消除最后一位的1,然后使用while循环判断什么时候为0即可。
```cpp
class Solution {
bool isPrime(int x) {
}if (x < 2) {return false;}for (int i = 2; i * i <= x; ++i) {if (x % i == 0) {return false;}}return true;
public: int countPrimeSetBits(int left, int right) { int ans = 0; for (int x = left; x <= right; ++x) { if (isPrime(__builtin_popcount(x))) { ++ans; } } return ans; } };
<a name="Tof2w"></a>
## 数字处理
<a name="KO91O"></a>
### [172. 阶乘后的零](https://leetcode-cn.com/problems/factorial-trailing-zeroes/)(递归写法)
这题想要知道后面有多少个零,只需要知道有多少个10,也就是5和2相乘即可,又因为2因子的数量远远大于5,因此只需要知道有多少个因子为5的数即可。<br />这题的难点在于要求时间复杂度为对数,必须使用递归来写。
- 这里的n/5D代表着所有的阶乘里面都分出一个5
- 新的n为n = n/5,代表着所有的阶层除去一个5之后的结果
- 递归调用。
```cpp
class Solution {
public:
// int trailingZeroes(int n) {
// return n == 0? 0:n/5+trailingZeroes(n/5);
// }
int trailingZeroes(int n){
if(n == 0) return 0;
return n/5+trailingZeroes(n);
}
};
504. 七进制数(标准进制转换)
- 如果返回值不是字符串类型,就应该思考超出范围的问题。因为10进制数转换为7进制数会使位数变多。
进制转换类的题,通常是通过触发和取模来写的。
class Solution { public: string convertToBase7(int num) { if(num == 0) return "0"; bool is_negative = num < 0;//代表是不是负数 if(is_negative) num = -num; string ans; while(num){ int a = num/7, b = num%7; ans = to_string(b) + ans; num = a; } return is_negative ? "-"+ ans: ans; } };168. Excel表列名称(进制转换变种)
这里注意,赋值等式不能同时有整型和string
和正常的0~25的26进制相比,本质上就是每一位多了1。假设 A == 0,B == 1,那么 AB = 26 0 + 1 1,而现在 AB = 26 (0 + 1) + 1 (1 + 1),所以只要在处理每一位的时候减 1,就可以按照正常的 26 进制来处理。
这里为什么是-1,是因为columnNumber本身就是 1~26转换之后的结果,换回去的话要-1;class Solution { public: string convertToTitle(int columnNumber) { string ans; while(columnNumber--){ ans += columnNumber % 26 + 'A'; columnNumber /= 26; } reverse(begin(ans), end(ans)); return ans; } };171. Excel 表列序号(上面一题的逆推)
和正常的0~25的26进制相比,就是每一位都多了1,因此每次转换都+1就行了。
class Solution { public: int titleToNumber(string columnTitle) { int n = columnTitle.size(); int ret = 0; for(int i = 0; i < n; i++){ ret += (columnTitle[i] - 'A' + 1)*pow(26 ,n-i -1); } return ret; } };415. 字符串相加
之所以将字符串reverse是因为,加法进位的形式是从后往前的。
- 设置一个位来表示进位
- 先计算对应的位,多出来的直接加上进位符号。
字符串表示数字加减法,还是通过减去’0’最为方便
class Solution { public: string addStrings(string num1, string num2) { string output(""); reverse(num1.begin(), num1.end()); reverse(num2.begin(), num2.end()); int onelen = num1.length(), twolen = num2.length(); if (onelen <= twolen){ swap(num1, num2); swap(onelen, twolen); }//始终保持第一个字符串最长。 int addbit = 0;//进位符 for (int i = 0; i < twolen; ++i){ int cur_sum = (num1[i]-'0') + (num2[i]-'0') + addbit; output += to_string((cur_sum) % 10); addbit = cur_sum < 10? 0: 1; } for (int i = twolen; i < onelen; ++i){ int cur_sum = (num1[i]-'0') + addbit; output += to_string((cur_sum) % 10); addbit = cur_sum < 10? 0: 1; } if (addbit) { output += "1"; } reverse(output.begin(), output.end());//最后反转回来。 return output; } };67. 二进制求和(字符串加法的变形题)
关键点还是在于设置addbit进位
- 果然还是使用-‘0’最为方便。
区别只是在这一题是二进制加法。
class Solution { public: string addBinary(string a, string b) { reverse(a.begin(), a.end()); reverse(b.begin(), b.end()); int addbit = 0, l1 = a.length(), l2 = b.length(); if(a.length() < b.length()){ swap(a, b); swap(l1, l2); } string res(""); for(int i = 0; i < l2; i++){ int sum = (a[i] - '0') + (b[i] - '0') + addbit; addbit = sum>=2; res += to_string(sum%2); } for(int i = l2; i < l1; i++){ int sum = (a[i]-'0') + addbit; addbit = sum>=2; res += to_string(sum%2); } if(addbit){ res += '1'; } reverse(res.begin(), res.end()); return res; } };326. 3 的幂(求n是否为3的幂次方)
class Solution { public: bool isPowerOfThree(int n) { return fmod(log10(n)/log10(3),1) == 0; //fmod就是取余的意思,但是返回值是double型的 //关于log函数的用法 //1.以e为底:log(n) //2.以10为底:log10(n) //3.以m为底:log(n)/log(m) } };1109.航班预定统计(差分数组)
差分数组里面存储的是每个值比前面一个值的差值。差分数组的作用在于,如果在一个区间添加增值的话,只需要改变两个值就可以完成这种改变
/* 原始数组 10 55 45 25 25 差分数组 10 45 -10 -20 0 在数组的 0-2号位置添加 10 原始数组 20 65 55 25 25 差分数组 20 45 -10 -30 0 只需要在 第0位置增加增值,在区间的后一位置减少增值 */ class Solution { public: vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) { vector<int> nums(n); for (auto& booking : bookings) { nums[booking[0] - 1] += booking[2]; if (booking[1] < n) { nums[booking[1]] -= booking[2]; }//想要改变一个区间的值的变化,差分数组仅仅只需要改变两个值。 } for (int i = 1; i < n; i++) { nums[i] += nums[i - 1]; } return nums; } };165.比较版本号(简单的进位处理)
这一题说实话想得复杂了,将一段纯数字字符串转换为正确的数字类型,只需要采取进位相加的方式就行了。
class Solution { public: int compareVersion(string version1, string version2) { int n = version1.size(), m = version2.size(); int i = 0, j = 0; while(i < n || j < m){ int num1 = 0; for(; i < n &&version1[i] != '.'; i++){ num1 = num1*10 + version1[i] - '0'; } i++; int num2 = 0; for(; j < m&&version2[j] != '.'; j++){ num2 = num2*10 + version2[j] - '0'; } j++; if(num1 != num2){ return num1 > num2 ? 1 : -1; } } return 0; } };随机与取样
384. 打乱数组(关键在于如何保存原数组)
为什么加上srand就会报错,至今仍然搞不懂
class Solution { vector<int> origin; public: Solution(vector<int> nums) { origin = std::move(nums);//能够减少内存占用,释放之前的内存。 } /** Resets the array to its original configuration and return it. */ vector<int> reset() { return origin; } /** Returns a random shuffling of the array. */ vector<int> shuffle() { //srand(time(0))随机数种子随时间变化,加上这个会报错 if(origin.empty()) return {}; vector<int> shuffled(origin); int n = shuffled.size(); for(int i = 0; i < n; i++){ swap(shuffled[i], shuffled[rand()%n]); } return shuffled; } };528. 按权重随机选择(前缀和来写)
我们可以先使用partial_sum求前缀和,这个结果对于正整数数组是单调递增的。每当需要采样时,我们可以先随机产生一个数字,然后使用二分法查找其在前缀和中的位置,以模拟加权采样的过程。
例如权重数组为[1,3]前缀和为[1,4]则只有为1时才选择1,为2,3,4,时位置为2; ```cpp class Solution { vectorsums; int sum; public: Solution(vector & w) { sums = w; partial_sum(sums.begin(), sums.end(), sums.begin());}
int pickIndex() {
int pos = (rand()%sums.back())+1;//随机取一个pos,pos范围是1-sums.back() vector<int>::iterator i = lower_bound(sums.begin(),sums.end(),pos) ; return i-sums.begin();} };
/**
- Your Solution object will be instantiated and called as such:
- Solution* obj = new Solution(w);
- int param_1 = obj->pickIndex();
*/
```
382. 链表随机节点(水库算法)
使用数组存储元素
```cpp class Solution { vectorarr;
public: Solution(ListNode *head) { while (head) { arr.emplace_back(head->val); head = head->next; } }
int getRandom() {
return arr[rand() % arr.size()];
}
};
<a name="R8Kw4"></a>
#### 水库算法
从链表头开始,遍历整个链表,对遍历到的第 ii 个节点,随机选择区间 [0,i)[0,i) 内的一个整数,如果其等于 00,则将答案置为该节点值,否则答案不变。<br />**意思就是说i之前的值是否被选中都不用管,只需要在意最后被选中的值,并且这个值之后都没有被选中。这样就能保证概率为1/N;**<br />该算法会保证每个节点的值成为最后被返回的值的概率均为 1/n;证明如下:<br />
```cpp
class Solution {
ListNode *head;
public:
Solution(ListNode *head) {
this->head = head;
}
int getRandom() {
int i = 1, ans = 0;
for (auto node = head; node; node = node->next) {
if (rand() % i == 0) { // 1/i 的概率选中(替换为答案)
ans = node->val;
}
++i;
}
return ans;
}
};
470. 用 Rand7() 实现 Rand10()(随机生成随机)
直接生成10次rand7取余(错误,但是可以过)
因为总共有7个0,6个1,数目就不同。
class Solution {
public:
int rand10() {
int sum;
for(int i = 0 ; i < 10; i++){
cout << rand7() << endl;
sum += rand7();
}
return sum%10 + 1 ;
}
};
拒绝采样
我们可以用拒绝采样的方法实现 \textit{Rand10()}Rand10()。在拒绝采样中,如果生成的随机数满足要求,那么就返回该随机数,否则会不断生成,直到生成一个满足要求的随机数为止
可以使用公式
已知 rand_N() 可以等概率的生成[1, N]范围的随机数 那么: (rand_X() - 1) × Y + rand_Y() ==> 可以等概率的生成[1, X * Y]范围的随机数 即实现了 rand_XY()class Solution { public: int rand10() { int row, col, idx; do { row = rand7(); col = rand7(); idx = col + (row - 1) * 7; } while (idx > 40); return 1 + (idx - 1) % 10; } };398. 随机数索引(水塘抽样)
哈系表
class Solution { private: unordered_map<int, vector<int>> hash; public: Solution(vector<int>& nums) { srand(time(NULL)); for(int i = 0; i < nums.size(); i++) { hash[nums[i]].emplace_back(i); } } int pick(int target) { int n = hash[target].size(); int idx = rand()%n; return hash[target][idx]; } };水塘抽样
有一个关键点是当rand()%i==0的时候不能直接返回,需要继续遍历完整个数组。
class Solution { vector<int> &nums; public: Solution(vector<int> &nums) : nums(nums) {} int pick(int target) { int ans; for (int i = 0, cnt = 0; i < nums.size(); ++i) { if (nums[i] == target) {//可以用公式推的,上面遇到过一次 ++cnt; // 第 cnt 次遇到 target if (rand() % cnt == 0) { ans = i;//注意这里不是直接返回,需要遍历完整个数组!!! } } } return ans; } };478. 在圆内随机生成点
拒绝采样
拒绝采样的意思是说,我们在一个更大的范围内生成随机数,并拒绝掉那些不在题目给定范围内的随机数,此时保留下来的随机数都是在范围内的。
这里的mt 19937, random_device,以及uniform_init_distribute都在下一题有详细说明。 ```cpp class Solution { private: mt19937 gen{random_device{}()}; uniform_real_distributiondis; double xc, yc, r;
public: Solution(double radius, double x_center, double y_center): dis(-radius, radius), xc(x_center), yc(y_center), r(radius) {}
vector<double> randPoint() {
while (true) {
double x = dis(gen), y = dis(gen);
if (x * x + y * y <= r * r) {
return {xc + x, yc + y};
}
}
}
};
<a name="dAh0v"></a>
#### 概率论写法(数学)
不会,不想复习,看链接<br />[https://leetcode.cn/problems/generate-random-point-in-a-circle/solution/zai-yuan-nei-sui-ji-sheng-cheng-dian-by-qp342/](https://leetcode.cn/problems/generate-random-point-in-a-circle/solution/zai-yuan-nei-sui-ji-sheng-cheng-dian-by-qp342/)
```cpp
class Solution {
private:
mt19937 gen{random_device{}()};
uniform_real_distribution<double> dis;
double xc, yc, r;
public:
Solution(double radius, double x_center, double y_center): dis(0, 1), xc(x_center), yc(y_center), r(radius) {}
vector<double> randPoint() {
double u = dis(gen), theta = dis(gen) * 2 * acos(-1.0);
double r = sqrt(u);
return {xc + r * cos(theta) * this->r, yc + r * sin(theta) * this->r};
}
};
剑指 Offer II 071. 按权重生成随机数(二分法+前缀和)
- 使用前缀和来保存权重
- 用二分法来查找
-
C++ 11
mt19937: 是指2^19937 -1 ,是一种随机数生成算法算法
random_device{}():可以生成真随机数,但是只在Linux下有效,因为LInux内核熵池,内核维护了一个熵池用来收集来自设备驱动程序和其它来源的环境噪音。理论上,熵池中的数据是完全随机的,可以实现产生真随机数序列。为跟踪熵池中数据的随机性,内核在将数据加入池的时候将估算数据的随机性,这个过程称作熵估算。熵估算值描述池中包含的随机数位数,其值越大表示池中数据的随机性越好。
uniform_int_distribution:离散均匀分布类(整数),使用方法就是输入参数为范围即可
uniform_real_distribution:离散均匀分布类(浮点数),需要模板参数 float或者double,然后同上。mt19937 gen{random_device{}()};//生成真随机数。 uniform_int_distribution dis(x, y);//离散均匀分布,范围是x到y dis(gen);//取一个范围为x和y的随机数。class Solution { private: mt19937 gen;//mt19937是c++ 11的新特性,是一种随机数算法。 uniform_int_distribution<int> dis;//离散均匀分布 vector<int> pre;//前缀和 //真随机数,只在Linux下random_device{}() public: //下面是制定uniform_init_distribution边界 Solution(vector<int>& w): gen(random_device{}()), dis(1, accumulate(w.begin(), w.end(), 0)) { partial_sum(w.begin(), w.end(), back_inserter(pre));//前缀和 } int pickIndex() { int x = dis(gen); return lower_bound(pre.begin(), pre.end(), x) - pre.begin();//二分法查找 } };普通写法
```cpp
class Solution {
private:
vector
public:
Solution(vector
int pickIndex() {
int rnd = rand() % total; //生成最大值范围内的随机数
int left = 0, right = sums.size() - 1;
while (left < right) //二分法在前缀和数组中找到第一个大于随机数的元素下标
{
int mid = left + (right - left) / 2;
if (rnd < sums[mid])
{
right = mid;
}
else
{
left = mid + 1;
}
}
return left;
}
};
<a name="mxsvk"></a>
### [497. 非重叠矩形中的随机点](https://leetcode.cn/problems/random-point-in-non-overlapping-rectangles/)
这题和上题非常类似,按照相应的权重生成随机数,使用前缀和+二分法来写!!!<br />维护一个前缀和数组,然后生成一个最大值范围内的随机数,使用二分法在找出第一个大于随机数的元素下标,然后常规随机就可以。
```cpp
class Solution {
public:
Solution(vector<vector<int>>& rects) : rects{rects} {
this->arr.emplace_back(0);
for (auto & rect : rects) {
this->arr.emplace_back(arr.back() + (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1));
}
}
vector<int> pick() {
uniform_int_distribution<int> dis(0, arr.back() - 1);//离散化分布
int k = dis(gen);
int rectIndex = upper_bound(arr.begin(), arr.end(), k) - arr.begin() - 1;//二分法判断,返回值为迭代器!!!
uniform_int_distribution<int> disx(rects[rectIndex][0], rects[rectIndex][2]);
uniform_int_distribution<int> disy(rects[rectIndex][1], rects[rectIndex][3]);
return {disx(gen), disy(gen)};
}
private:
vector<int> arr;//前缀和数组
vector<vector<int>>& rects;
mt19937 gen{random_device{}()};
};
循环
238. 除自身以外数组的乘积(可以看)
关键在于怎么实现常数空间复杂度,注意边界的情况。不要考虑超出范围的问题!!!每个数组的意义就限制在自己的意义之内
class Solution {
public:
vector<int> productExceptSelf(vector<int>& nums) {
int length = nums.size();
vector<int> answer(length);
// answer[i] 表示索引 i 左侧所有元素的乘积
// 因为索引为 '0' 的元素左侧没有元素, 所以 answer[0] = 1
answer[0] = 1;
for (int i = 1; i < length; i++) {
answer[i] = nums[i - 1] * answer[i - 1];
}
// R 为右侧所有元素的乘积
// 刚开始右边没有元素,所以 R = 1
int R = 1;
for (int i = length - 1; i >= 0; i--) {
// 对于索引 i,左边的乘积为 answer[i],右边的乘积为 R
answer[i] = answer[i] * R;
// R 需要包含右边所有的乘积,所以计算下一个结果时需要将当前值乘到 R 上
R *= nums[i];
}
return answer;
}
};
462. 最少移动次数使数组元素相等 II(数学的魅力)
链接:https://leetcode-cn.com/problems/minimum-moves-to-equal-array-elements-ii/solution/czhong-wei-shu-jian-dan-zheng-ming-by-ke-a2v9/
根据证明可得这个元素x就是数组的中位数。
- 首先根据数组长度得出n/2
- 然后通过快排算法 将 n/2处的元素前面都小于它,后面都大于它
- 相减取绝对值即可。
class Solution { public: int minMoves2(vector<int> &nums) { int mid = static_cast<int>(nums.size()) / 2, ans = 0; nth_element(begin(nums), next(begin(nums), mid), end(nums)); for_each(begin(nums), end(nums), [&](int num) { ans += abs(num - nums[mid]); }); return ans; } };
492. 构造矩形(简单)
笨比写法
class Solution {
public:
vector<int> constructRectangle(int area) {
int l, w, mins = 10000000, num = area;
for(int i = 1; i <= sqrt(area); i++){
if(area%i == 0){
w = i, l = (area/i);
if((l - w) < mins){
mins = (l - w);
num = i;
}
}
}
return {area/num, num};
}
};
优化写法
class Solution {
public:
vector<int> constructRectangle(int area) {
int w = sqrt(1.0 * area);
while (area % w) {
--w;
}
return {area / w, w};
}
};
//直接从中间开始遍历就行了
202. 快乐数(快慢指针)
判断循环就使用快慢指针,额外写一个函数用来计算平方数。还是要交经常想着额外写一个函数。
有三种情况
- 终点为1
- 陷入循环
- 无限大(不可能发生)
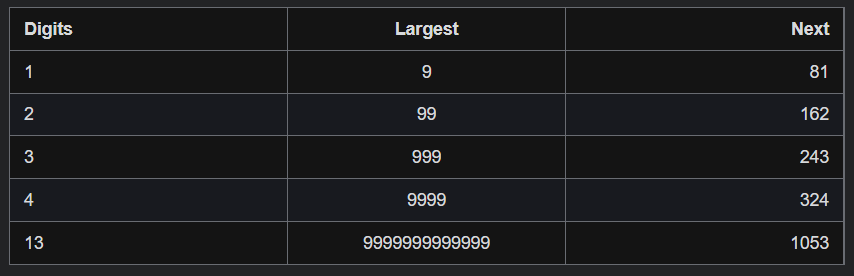
对于 33 位数的数字,它不可能大于 243243。这意味着它要么被困在 243243 以下的循环内,要么跌到 11。44 位或 44 位以上的数字在每一步都会丢失一位,直到降到 33 位为止。所以我们知道,最坏的情况下,算法可能会在 243243 以下的所有数字上循环,然后回到它已经到过的一个循环或者回到 11。但它不会无限期地进行下去,所以我们排除第三种选择。
class Solution {
public:
int bitSquareSum(int n) {
int sum = 0;
while(n > 0)
{
int bit = n % 10;
sum += bit * bit;
n = n / 10;
}
return sum;
}
bool isHappy(int n) {
int slow = n, fast = n;
do{
slow = bitSquareSum(slow);
fast = bitSquareSum(fast);
fast = bitSquareSum(fast);
}while(slow != fast);
return slow == 1;
}
};
31. 下一个排列
这一题的要求是给你一个数字,要求你输出比本数组大的最小的排列方式
- 想法就是将一大一小两个数字互换,小的数字是尽可能靠右的,大的数字是尽可能晓得。
- 因此得到规则,小的选择第一个比后面的数字小的,大的选择后面比小的大的倒数第一个数字。
- 结束之后,将小数字后面的部分反转,让后面的情况最小。
如果已经是最大的情况,那么此时小的数字的位置为-1,直接把整个数组进行reverse
class Solution { public: void nextPermutation(vector<int>& nums) { int i = nums.size() - 2; while (i >= 0 && nums[i] >= nums[i + 1]) { i--; } if (i >= 0) { int j = nums.size() - 1; while (j >= 0 && nums[i] >= nums[j]) { j--; } swap(nums[i], nums[j]); } reverse(nums.begin() + i + 1, nums.end()); } };算法
780. 到达终点(倒序)
这题使用正向计算情况非常多,可能会超出时间限制,因此这里使用反向计算,可能的情况如下
- 如果tx = ty,则不存在上一个状态,因为tx和ty都只能加对方,不能自己加。
- 如果tx > ty, 则一定是由tx = tx+ty 这样子过来的,所以反向推理,tx = tx%ty,因为可能多加多个ty
- 如果tx < ty,则一定是由ty = ty+tx 这样子过来的,所以反向推理,ty = ty%tx,因为可能加多个tx
当反向操作不成立时,又有以下几种情况
- 如果tx=sx 且 ty=sy,则已经到达起点状态,因此可以从起点转换到终点。
- 如果tx = sx 且ty!=sy,则tx不能继续减小,只能减小ty,因此只有当ty>sy且(ty-sy)mod tx = 0时是可达的。
- 如果tx!=sx且ty = sy,则ty不能继续减小,只能减小tx,因此只有当tx>sx且(tx - sx)lmod ty = 0时是可达的。
如果两个都不等,则不可以从起点转换到终点。
class Solution { public: bool reachingPoints(int sx, int sy, int tx, int ty) { while (tx > sx && ty > sy && tx != ty) { if (tx > ty) { tx %= ty; } else { ty %= tx; } } if (tx == sx && ty == sy) { return true; } else if (tx == sx) { return ty > sy && (ty - sy) % tx == 0; } else if (ty == sy) { return tx > sx && (tx - sx) % ty == 0; } else { return false; } } };357. 统计各位数字都不同的数字个数(排列组合)
不用返回所有情况的集合,所以直接排列组合就行了。
- 高中的排列组合题目,相当于把每个位的可能情况加起来
- 1时是10个,2是9×9,因为第一位不能为0,如果为0就是1位数了。
3是9×9×8,4是9×9×8×7
class Solution { public: int countNumbersWithUniqueDigits(int n) { if (n == 0) { return 1; } if (n == 1) { return 10; } int ans = 10, cur = 9; for (int i = 0; i < n - 1; ++i) { cur *= 9 - i; ans += cur; } return ans; } };479. 最大回文数乘积
先枚举左半部分,同时由于两个n位整数的乘积最多是个2n位数,我们可以从pow(10, n)-1来开始枚举回文数的左半部分
得到回文数p后,需要判断是否能分解成两个n位整数。可以从pow(10, n) - 1开始从大到小 枚举x,若x能整除p且x和p/x均为整数,则p就是我们要找的答案。注意枚举到根号p即可。
class Solution { public: int largestPalindrome(int n) { if (n == 1) {//特殊情况 return 9; } int upper = pow(10, n) - 1; for (int left = upper;; --left) { // 枚举回文数的左半部分 long p = left; for (int x = left; x > 0; x /= 10) {//左半部分回文串得到整个回文串。 p = p * 10 + x % 10; // 翻转左半部分到其自身末尾,构造回文数 p } for (long x = upper; x * x >= p; --x) {//这里的x取值最大为根号p,因此x一定是n位数 if (p % x == 0) { // x 是 p 的因子 return p % 1337; } } } } };1037. 有效的回旋镖(判断三点是否共线)
注意将求斜率是否相等用乘法来表示。
class Solution { public: bool isBoomerang(vector<vector<int>>& points) { int x1 = points[0][0] - points[1][0]; int y1 = points[0][1] - points[1][1]; int x2 = points[1][0] - points[2][0]; int y2 = points[1][1] - points[2][1]; if(x1*y2 == x2*y1) return false; else return true; } };数组
396. 旋转函数
找规律,相邻数组之间的关系
- sum = sum - vsum + n×pre
- 其中pre就是前一个数组的开头
class Solution { public: int maxRotateFunction(vector<int>& nums) { int n = nums.size(), sum = 0; int vsum = accumulate(nums.begin(), nums.end(), 0); int pre = nums[0]; for(int i = 0; i < n; i++) { sum += i*nums[i]; } int ret = sum; for(int i = 1; i < n; i++) { sum = sum - vsum + n*pre; pre = nums[i]; ret = max(sum, ret); } return ret; } };

