- 一维
- 198. 打家劫舍">198. 打家劫舍
- 213. 打家劫舍 II(首尾相连,值得看)">213. 打家劫舍 II(首尾相连,值得看)
- 70. 爬楼梯(经典一维)">70. 爬楼梯(经典一维)
- 53. 最大子数组和(可以看)">53. 最大子数组和(可以看)
- 413. 等差数列划分(特殊)">413. 等差数列划分(特殊)
- 338. 比特位计数(位运算,二进制)">338. 比特位计数(位运算,二进制)
- 467. 环绕字符串中唯一的子字符串(含金量太重了)">467. 环绕字符串中唯一的子字符串(含金量太重了)
- 二维
- 64. 最小路径和(经典二维)">64. 最小路径和(经典二维)
- 542. 01 矩阵(贪心+动规)">542. 01 矩阵(贪心+动规)
- 分割类问题
- 279. 完全平方数">279. 完全平方数
- 139. 单词拆分(与完全平方数类似)">139. 单词拆分(与完全平方数类似)
- 91. 解码方法(分清楚情况)">91. 解码方法(分清楚情况)
- 343. 整数拆分(巧妙)">343. 整数拆分(巧妙)
- 646. 最长数对链(标准分割问题)">646. 最长数对链(标准分割问题)
- 2312. 卖木头块(周赛题目)">2312. 卖木头块(周赛题目)
- 子序列问题
- 300. 最长递增子序列(二分优化,重点)">300. 最长递增子序列(二分优化,重点)
- 446等差数列划分Ⅱ 子序列:
- 1143公共子序列 :
- 583. 两个字符串的删除操作(公共子序列的变形题目)">583. 两个字符串的删除操作(公共子序列的变形题目)
- 516最长回文子序列
- 5.最长回文子串
- 647. 回文子串(求个数)">647. 回文子串(求个数)
- 背包问题
- 01背包问题
- 完全背包问题
- 416. 分割等和子集">416. 分割等和子集
- 474. 一和零(三维01背包问题)">474. 一和零(三维01背包问题)
- 494. 目标和(特殊模式的01背包问题)">494. 目标和(特殊模式的01背包问题)
- 322. 零钱兑换(完全背包问题)">322. 零钱兑换(完全背包问题)
- 871. 最低加油次数(另类背包问题)">871. 最低加油次数(另类背包问题)
- 字符串编辑问题
- 72. 编辑距离(多种情况)">72. 编辑距离(多种情况)
- 650. 只有两个键的键盘(和之前的分割问题很像)">650. 只有两个键的键盘(和之前的分割问题很像)
- 10. 正则表达式匹配">10. 正则表达式匹配
- 股票交易
- 状态压缩
- 1494. 并行课程 II(华为机式)">1494. 并行课程 II(华为机式)
- 特殊情况
- 552学生出勤记录Ⅱ
- 1218. 最长定差子序列(dp+哈希)">1218. 最长定差子序列(dp+哈希)
- 375. 猜数字大小 II(重点)">375. 猜数字大小 II(重点)
- 6109. 知道秘密的人数(周赛题目)">6109. 知道秘密的人数(周赛题目)
一维
198. 打家劫舍
class Solution {public:int rob(vector<int>& nums) {int n = nums.size();vector<int> dp(n+1);dp[1] = nums[0];for(int i = 2; i <= n; i++){dp[i] = max(dp[i-1], dp[i-2]+nums[i-1]);}return dp[n];}};
213. 打家劫舍 II(首尾相连,值得看)
- 这一题与上一题不同的是首尾相连,如果同时选择了头和尾的情况也会触发报警
- 这一题思考的角度非常关键,将总情况分为两个互不干涉的子集。
分别是1~n以及0~n-1,然后分别进行动态规划
class Solution {public:int robRange(vector<int>& nums, int start, int end) {vector<int> dp(nums.size()+1);dp[start+1] = nums[start];for(int i = start + 2; i <= end; i++){dp[i] = max(dp[i-1], dp[i-2] + nums[i-1]);}return dp[end];}int rob(vector<int>& nums) {int length = nums.size();if (length == 1) {return nums[0];} else if (length == 2) {return max(nums[0], nums[1]);}return max(robRange(nums, 0, length - 1), robRange(nums, 1, length));}};
空间压缩
class Solution {public:int robRange(vector<int>& nums, int start, int end) {int first = nums[start], second = max(nums[start], nums[start + 1]);for (int i = start + 2; i <= end; i++) {int temp = second;second = max(first + nums[i], second);first = temp;}return second;}int rob(vector<int>& nums) {int length = nums.size();if (length == 1) {return nums[0];} else if (length == 2) {return max(nums[0], nums[1]);}return max(robRange(nums, 0, length - 2), robRange(nums, 1, length - 1));}};
70. 爬楼梯(经典一维)
class Solution { public: int climbStairs(int n) { vector<int> dp(n+1,1); for(int i=2 ;i<=n ;i++){ dp[i] = dp[i-1] + dp[i-2];//只要最后一步不一样就是两种不同的方法 } return dp[n]; } };53. 最大子数组和(可以看)
注意这里的转移方程,dp[i]只能代表以i为结尾的子串的最大值!!!并且num[i]必须要选,也就是说dp[i]表示的子串必须以num[i]为结尾!!!
- 因为如果dp[i]表示i之前的最大值,那么子集与父集之间的关系将会非常难找。
先明确dp代表什么,然后在明确状态转移方程。!!!!
class Solution { public: int maxSubArray(vector<int>& nums) { int n = nums.size(), res = INT_MIN/2; vector<int> dp(n+1); for(int i = 1; i <= n; i++){ dp[i] = max(dp[i-1] + nums[i-1], nums[i-1]); res = max(res, dp[i]); } return res; } };413. 等差数列划分(特殊)
class Solution { public: int numberOfArithmeticSlices(vector<int>& nums) { int n = nums.size(); vector<int> dp(n); for(int i = 2 ; i < n ; i++){ dp[i] = (nums[i - 1] - nums[i - 2] == nums[i] - nums[i - 1])? dp[i-1] + 1 : 0; } return accumulate(dp.begin(), dp.end(), 0); } };338. 比特位计数(位运算,二进制)
巧妙,只能说巧妙
分为两种情况,最低位为1和最低位为0。最低位为1的话就代表i-1的最低位为零,直接dp[i-1]即可
- 最低位为0的话,经过移位1的数量不变,因此直接dp[i>>1]即可
```cpp
class Solution {
public:
vector
countBits(int num) {
}vector<int> dp(num+1, 0); for(int i = 1; i <= num; ++i) dp[i] = i & 1? dp[i-1] + 1: dp[i>>1];//往左移动一位相当于变小,因为最后一位是0所以1的个数并没有发生改变 return dp;
};
<a name="EFTOs"></a>
### [313. 超级丑数](https://leetcode-cn.com/problems/super-ugly-number/)(太细节拉)
- 这里的想法是,每一个后面的数都是由前面的数 × primes里面的元素来得到的
- 因此维护m个指针,分别用这个m个指针乘235来然后其中最小的数就是结果
- **这些指针代表,还没有乘对应的primes的最小位置**
- **注意这里的优化方法,将下一次乘之后的值存进nums,这样可以减少复杂度,减少一次乘运算**
```cpp
class Solution {
public:
int nthSuperUglyNumber(int n, vector<int>& primes) {
vector<long> dp(n + 1);
int m = primes.size();
vector<int> pointers(m, 0);
vector<long> nums(m, 1);
for (int i = 1; i <= n; i++) {
long minNum = INT_MAX;
for (int j = 0; j < m; j++) {
minNum = min(minNum, nums[j]);//直接使用下一次位置之后的最小值。
}
dp[i] = minNum;//赋值给dp
for (int j = 0; j < m; j++) {
if (nums[j] == minNum) {//只有选择过的对应的位置才会进行指针加1,以及维护nums数组。
pointers[j]++;
nums[j] = dp[pointers[j]] * primes[j];//将后面的数都存进nums,只有选取过之后才会更新nums对应的位置
}
}
}
return dp[n];
}
};
467. 环绕字符串中唯一的子字符串(含金量太重了)
- 对于两个以同一个字符结尾的子串,长的那个必定包含短的那个
- dp[i]表示以’a’+i为结尾的最长长度
- abcd的子串为 abcd,bcd,cd,d。都包含结尾,因此按照结尾来区分dp元素不会重复
字符之差为 1 或 -25,就是相邻的意思,这是因为s为无线环绕字符串,首位相连。
class Solution { public: int findSubstringInWraproundString(string p) { //按照不同的结尾来区分!!! //abcd的子串为 abcd,bcd,cd,d。都包含结尾,因此按照结尾来区分dp元素不会重复 vector<int> dp(26);//dp[i]表示以'a'+i为结尾的最长长度。 int k = 0;//k应该代表前一个字符串的长度 for (int i = 0; i < p.length(); ++i) { if (i && (p[i] - p[i - 1] + 26) % 26 == 1) { // 字符之差为 1 或 -25,就是相邻的意思 ++k; } else { k = 1; } dp[p[i] - 'a'] = max(dp[p[i] - 'a'], k);//每个dp[i]中保存的都是以该字母结尾的最长长度。因为长的肯定包括短的 } return accumulate(dp.begin(), dp.end(), 0); } };二维
64. 最小路径和(经典二维)
class Solution { public: int minPathSum(vector<vector<int>>& grid) { int n = grid.size(), m = grid[0].size(); vector<vector<int>> dp(n+1, vector<int>(m+1)); for(int i = 1; i <= n ; i++){ for(int j = 1; j <= m; j++){ int num = grid[i-1][j-1]; if(i == 1){ dp[i][j] = dp[i][j-1] + num; } else if(j == 1){ dp[i][j] = dp[i-1][j] + num; } else { dp[i][j] = min(dp[i][j-1], dp[i-1][j]) + num; } } } return dp[n][m]; } };542. 01 矩阵(贪心+动规)
与135非常像。就是135的动规版本。
先从左上到右下
- 在从右下到左上
- 可以这样理解,从最近的0走到1,肯定只能从1周围上下左右4个点走到1,第一次从左上角到右下角遍历整个表,到表中任意位置i的时候,i上方和左方的位置已经遍历过了,所以可以判断从上方进入这个1和左方进入这个1的状况哪个最近,并在dp数组保存。同理,第二次从右下角到左上角遍历整个表到i位置时,i右方和下方的位置状态已经更新过了,所以能判断从右边进入合算还是从下边进入合算,再加上第一次遍历保存的左方和上方的最优解就能判断出上下左右四个方向的最优解了
第一个元素没有左边也没有上边,或者说左上方没有0,所以第一次遍历的时候,计算从它左上角最近的0到它的距离是无穷大,这个没有问题
class Solution { public: vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) { if(matrix.empty()) return {}; int n= matrix.size(),m=matrix[0].size(); vector<vector<int>> dp(n,vector<int>(m, INT_MAX-1)); for(int i=0;i<n;i++){ for(int j=0;j<m;j++){ if(matrix[i][j]==0){ dp[i][j] =0; } else { if(j>0){ dp[i][j]=min(dp[i][j],dp[i][j-1]+1); } if(i>0){ dp[i][j]=min(dp[i][j],dp[i-1][j]+1); } } } } for(int i=n-1;i>=0;--i){ for(int j=m-1;j>=0;--j){ if(matrix[i][j]!=0){ if(j<m-1){ dp[i][j]=min(dp[i][j],dp[i][j+1]+1); } if(i<n-1){ dp[i][j]=min(dp[i][j],dp[i+1][j]+1); } } } } return dp; } };分割类问题
对于分割类问题,动态规划的状态转移方程通常并不依赖相邻的位置,而是依赖于满足分割条件的位置。
279. 完全平方数
class Solution { public: int numSquares(int n) { vector<int> dp(n+1,INT_MAX); dp[0]=0; for(int i =1;i<=n;i++){ for(int j = 1;j*j<=i;j++){ dp[i] = min(dp[i],dp[i-j*j]+1); } } return dp[n]; } };139. 单词拆分(与完全平方数类似)
dp[n]代表从1到n能否使用字典中出现的单词拼接。
策略类似完全平方数,for里面嵌套一个循环来查找字典中的单词。class Solution { public: bool wordBreak(string s, vector<string>& wordDict) { int n = s.length(); vector<bool> dp(n+1,false); dp[0] = true; for(int i =1;i<=n;++i){ for(auto word : wordDict){ int len = word.length(); if(i>=len&&s.substr(i-len,len) == word){ dp[i] = dp[i] || dp[i - len]; } } } return dp[n]; } };91. 解码方法(分清楚情况)
这是一道很经典的动态规划题,难度不大但是非常考验耐心。
- 这是因为只有1-26可以表示字母,因此对于一些特殊情况,比如数字0,或者相邻两数字大于26时,需要有不同的状态转移方程。
可以使用一个pre和cur来存储相邻两个元素。
class Solution { public: int numDecodings(string s) { int n = s.size(); if(n == 0) return 0; int prev = s[0] - '0'; if(!prev) return 0;//这是因为'0'开头不可能符合任何情况。 if(n == 1) return 1; vector<int> dp(n+1,1); for(int i = 2;i<=n;++i){ int cur = s[i-1] - '0'; if((prev== 0||prev >2)&&cur == 0){//不可能的特殊情况,予以排除。 return 0; } if((prev<2&& prev>0)||prev == 2&&cur < 7){ if(cur){ dp[i] = dp[i-2] +dp[i-1]; } else { dp[i] = dp[i-2]; } } else { dp[i] = dp[i-1]; } prev = cur ; } return dp[n]; } };343. 整数拆分(巧妙)
分割的第二次循环的选取非常重要
一定要注意突出子集与父集之间对应的关系
思路:
对于正整数n,当n>=2时,可以拆分成至少两个正整数的和。令k是拆分出的第一个正整数,则剩下的部分是n-k,n-k可以不继续拆分,或者继续拆分成至少两个正整数的和。由于每个正整数对应的最大乘积取决于比他小的正整数对应的最大乘积,因此使用动态规划。class Solution { public: int integerBreak(int n) { vector <int> dp(n + 1); for (int i = 2; i <= n; i++) { int curMax = 0; for (int j = 1; j < i; j++) { curMax = max(curMax, max(j * (i - j), j * dp[i - j])); } dp[i] = curMax; } return dp[n]; } };646. 最长数对链(标准分割问题)
每个子集的结果取决于前面所有子集的结果。
class Solution { public: int findLongestChain(vector<vector<int>>& pairs) { sort(pairs.begin(), pairs.end(), [](vector<int> &a, vector<int>b) { if (a[0] == b[0]) return a[1] < b[1]; return a[0] < b[0]; }); int n = pairs.size(), ans = 1; vector<int> dp(n, 1); for (int i = 1; i < n; i++) { dp[i] = 1; for (int j = 0; j < i; j++) { if (pairs[i][0] > pairs[j][1]) dp[i] = max(dp[i], dp[j] + 1); } ans = max(ans, dp[i]); } return ans; } };2312. 卖木头块(周赛题目)
千万要注意父集从子集考虑,而不要子集往父集推。先考虑dp[i][j]是从什么得来的。
这里的dp[i][j]可以从两个维度进行分割成子集,求最大值即可。class Solution { public: long long sellingWood(int n, int m, vector<vector<int>>& prices) { // 记录直接卖的收益 vector<vector<int>> A; A.resize(n + 1, vector<int>(m + 1)); for (auto &vec : prices) A[vec[0]][vec[1]] = vec[2]; vector<vector<long long>> f;//第一位x轴,第二位y轴 f.resize(n + 1, vector<long long>(m + 1)); for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) { // 直接卖 f[i][j] = A[i][j]; // 沿水平方向分割 for (int k = 1; k < i; k++) f[i][j] = max(f[i][j], f[k][j] + f[i - k][j]); // 沿垂直方向分割 for (int k = 1; k < j; k++) f[i][j] = max(f[i][j], f[i][k] + f[i][j - k]); } return f[n][m]; } };子序列问题
300. 最长递增子序列(二分优化,重点)
O(n2)时间复杂度
class Solution { public: int lengthOfLIS(vector<int>& nums) { int n = nums.size(), res = 0; vector<int> dp(n+1, 1); for(int i = 1; i <= n; i++){ for(int j = 1; j < i; j++){ if(nums[i-1] > nums[j-1]){ dp[i] = max(dp[j]+1, dp[i]); } } res = max(dp[i], res); } return res; } };O(nlogn)时间复杂度
可以使用二分查找将时间复杂度降低为O(nlogn)。
- 定义一个dp数组,其中dp[k]存储长度为k+1的最长递增子序列的最后一个数字。我们遍历每一个位置i,如果其对应的数字大于dp数组中的所有数字的值,那么我们把它放到dp数组的尾部,表示最长递增子序列长度加1;
如果我们发现这个数字在dp数组中比数字a大、比数字b小,则我们将b更新为此数字,使得之后哦古城底层序列的可能性增大。这种方式维护的dp数组永远是递增的,因此可以用二分加速搜索。
class Solution { public: int lengthOfLIS(vector<int>& nums) { int n = nums.size(); if(n <= 1) return n; vector<int> dp; dp.push_back(nums[0]); for(int i = 1; i < n; i++){ if(dp.back() < nums[i]){ dp.push_back(nums[i]); } else { auto itr = lower_bound(dp.begin(), dp.end(), nums[i]); *itr = nums[i];//这个部分非常关键,这是拥有普适性的关键。 } } return dp.size(); } };446等差数列划分Ⅱ 子序列:
想法非常重要,因为题目要求的
-231 <= nums[i] <= 231 - 1,超出了int所以使用long long类型- 将f[i][d]表示为尾项为nums[i]公差为d的若等差子序列的个数
如果后面出现了公差为d的则加上之前的若等差子序列,就成为了标准等差数列。
class Solution { public: int numberOfArithmeticSlices(vector<int> &nums) { int ans = 0; int n = nums.size(); vector<unordered_map<long long, int>> f(n);//动规的第二位用hash表来代替 for (int i = 0; i < n; ++i) { for (int j = 0; j < i; ++j) { long long d = 1LL * nums[i] - nums[j]; auto it = f[j].find(d); int cnt = it == f[j].end() ? 0 : it->second; ans += cnt;//有多少个若等差数列,就能与当前的这个元素组成多少个标准等差数列 f[i][d] += cnt + 1 ;//这里面存的是弱等差数列的个数。 } } return ans; } };1143公共子序列 :
找到两个最长公共子序列使用二维动态规划
对于子序列问题,第二种动态规划方法是,定义一个dp数组,其中dp[i]表示到位置为止的子序列的性质。
- 本题中,我们建立一个二维数组,其中dp[i][j]表示到第一个字符串位置i为止、到第二个字符串位置j为止、最长子序列长度。
class Solution { public: int longestCommonSubsequence(string text1, string text2) { int n = text1.size(); int m = text2.size(); vector<vector<int>> dp(n+1,vector<int>(m+1,0)); for(int i = 1;i <= n ; i++){ for(int j = 1; j <= m; j++ ){ if(text1[i-1] == text2[j-1]) dp[i][j] = dp[i-1][j-1] + 1;//这里隐含着dp[i-1][j]与dp[i][j-1]不可能大于dp[i][j],所以不用判断。 else dp[i][j] = max(dp[i-1][j],dp[i][j-1]);//严格按照逻辑来,这里dp[i-1][j-1]不可能大于dp[i-1][j]与dp[i][j-1]; } } return dp[n][m]; } };583. 两个字符串的删除操作(公共子序列的变形题目)
转移方程为 ```cppif(word1[i-1] == word2[j-1]){ dp[i][j] = dp[i-1][j-1] + 1; } else { dp[i][j] = max(dp[i-1][j-1], max(dp[i-1][j], dp[i][j-1])); }
代码
```cpp
class Solution {
public:
int minDistance(string word1, string word2) {
int n = word1.size(), m = word2.size(), maxs = 0;
vector<vector<int>> dp(n + 1, vector<int>(m + 1));
for(int i = 1; i <= n; i++){
for(int j = 1; j <=m; j++){
if(word1[i-1] == word2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
} else {
dp[i][j] = max(dp[i-1][j-1], max(dp[i-1][j], dp[i][j-1]));
}
maxs = max(dp[i][j], maxs);
}
}
return n+m-2*maxs;
}
};
516最长回文子序列
在一个数组中找到一个最长的回文字串,这里子串可以不是连续的。使用动态规划的一个大的特点是,一定可以把大的问题分解成小的问题。并且,可以得出状态转移方程。
class Solution {
public:
int longestPalindromeSubseq(string s) {
int n = s.length();
vector<vector<int>> dp(n, vector<int>(n));
for (int i = n - 1; i >= 0; i--) {
dp[i][i] = 1;
char c1 = s[i];
for (int j = i + 1; j < n; j++) {
char c2 = s[j];
if (c1 == c2) {
dp[i][j] = dp[i + 1][j - 1] + 2;
} else {
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
}
return dp[0][n - 1];
}
};
//类似数组的想法,一般用到dp[i][j],i < j,然后慢慢扩散,注意看回文串的特点。
5.最长回文子串
本题与上一题最大的区别在于,上一题的子序列可以不是连续的,并且返回的是int类型的最大长度,而本题返回的是字符串。毫无疑问,这一题难度更大。
动态规划写法(特别)
- 这一题的动态规划写法非常的特别,使用回文串的长度L作为最外层的循环,第二层的循环为左边界i,j通过i与L的关系来计算,以此来遍历所有情况。
- 里面的条件判断存在一些小技巧,当s[i]==s[j]时,当该长度大于3时,与小于3时情况不一样。
- 定义dp[i][j]为true或者false代表以i-j的范围是否是回文串。返回字符串的解决方式,每次为回文串时都做一次记录,保留最长的情况。 ```cpp
class Solution { public: string longestPalindrome(string s) { int n = s.size(); if (n < 2) { return s; }
int maxLen = 1;
int begin = 0;
// dp[i][j] 表示 s[i..j] 是否是回文串
vector<vector<int>> dp(n, vector<int>(n));
// 初始化:所有长度为 1 的子串都是回文串
for (int i = 0; i < n; i++) {
dp[i][i] = true;
}
// 递推开始
// 先枚举子串长度
for (int L = 2; L <= n; L++) {
// 枚举左边界,左边界的上限设置可以宽松一些
for (int i = 0; i < n; i++) {
// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得,此处的L为回文串长度
int j = L + i - 1;
// 如果右边界越界,就可以退出当前循环
if (j >= n) {
break;
}
if (s[i] != s[j]) {
dp[i][j] = false;
} else {
if (j - i < 3) {
dp[i][j] = true;
} else {
dp[i][j] = dp[i + 1][j - 1];
}
}
// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置
if (dp[i][j] && j - i + 1 > maxLen) {
maxLen = j - i + 1;
begin = i;
}
}
}
return s.substr(begin, maxLen);
}
};
<a name="Kb9Xw"></a>
#### 中心扩散算法
这种算法在这一题的情况来说,毫无疑问是最优解。
- 先确定回文串的中心在进行两边扩散,中心就是i=j,或者i = j-1这两种情况。
- 写一个扩散函数来进行扩散,找到以当前为中心的最大字串
- 中心有两种情况,分别为相等和相邻
```cpp
class Solution {
public:
pair<int, int> expandAroundCenter(const string& s, int left, int right) {
while (left >= 0 && right < s.size() && s[left] == s[right]) {
--left;
++right;
}
return {left + 1, right - 1};
}
string longestPalindrome(string s) {
int start = 0, end = 0;
for (int i = 0; i < s.size(); ++i) {
auto [left1, right1] = expandAroundCenter(s, i, i);
auto [left2, right2] = expandAroundCenter(s, i, i + 1);
if (right1 - left1 > end - start) {//选出最长的情况
start = left1;
end = right1;
}
if (right2 - left2 > end - start) {
start = left2;
end = right2;
}
}
return s.substr(start, end - start + 1);
}
};
647. 回文子串(求个数)
这题和最长回文串唯一不同的地方就是这题求得是个数,而最长回文串求的是长度。
- 先把每个位置都遍历一遍,i,j如果是true则加1即可
class Solution { public: int countSubstrings(string s) { int n = s.size(),res = 0; if(n < 2){ return n; } vector<vector<int>> dp(n, vector<int>(n)); for(int i = 0; i < n; i++){ dp[i][i] = true; res++; } for(int i = n-1; i >= 0; i--){ for(int j = i+1; j < n ; j++){ if(s[i] == s[j]){ if((j-i)<=2){ dp[i][j] = true; } else { dp[i][j] = dp[i+1][j-1]; } } else { dp[i][j] = false; } if(dp[i][j]){ res++; } } } return res; } };中心扩散
class Solution { public: int countSubstrings(string s) { int count = 0; for(int i = 0; i < s.size(); i++){ count += ext(s, i, i);//有一个中心,也就是说长度为奇数 count += ext(s, i, i + 1);//有两个中心,也就是说长度为偶数 } return count; } int ext(string s, int l , int r){ int count = 0; while(l >= 0&& r < s.size()&&s[l] == s[r]){ --l; ++r; ++count; } return count; } }; //有一说一想法还挺奇特,确实中点定了之后,每个子集并不相交 //与之前的dp法相比,没有浪费额外的空间,也没有遍历多余的子集
背包问题
01背包问题
int knapsack(vector<int> weights, vector<int> values, int N, int W){
vector<vector<int>> dp(N+1, vector<int>(W+1, 0));
for(int i = 0; i < N; i++){
int w = weights[i-1], v = values[i-1];
for(int j = 0; j < M; j++){
if(j >= w){
dp[i][j] = max(dp[i-1][j], dp[i-1][j-v]+w);
} else {
dp[i][j] = dp[i-1][j];
}
}
}
return dp[N][M];
}
完全背包问题
相对0-1背包问题,完全背包问题的不同就是同一个物品可以重复选。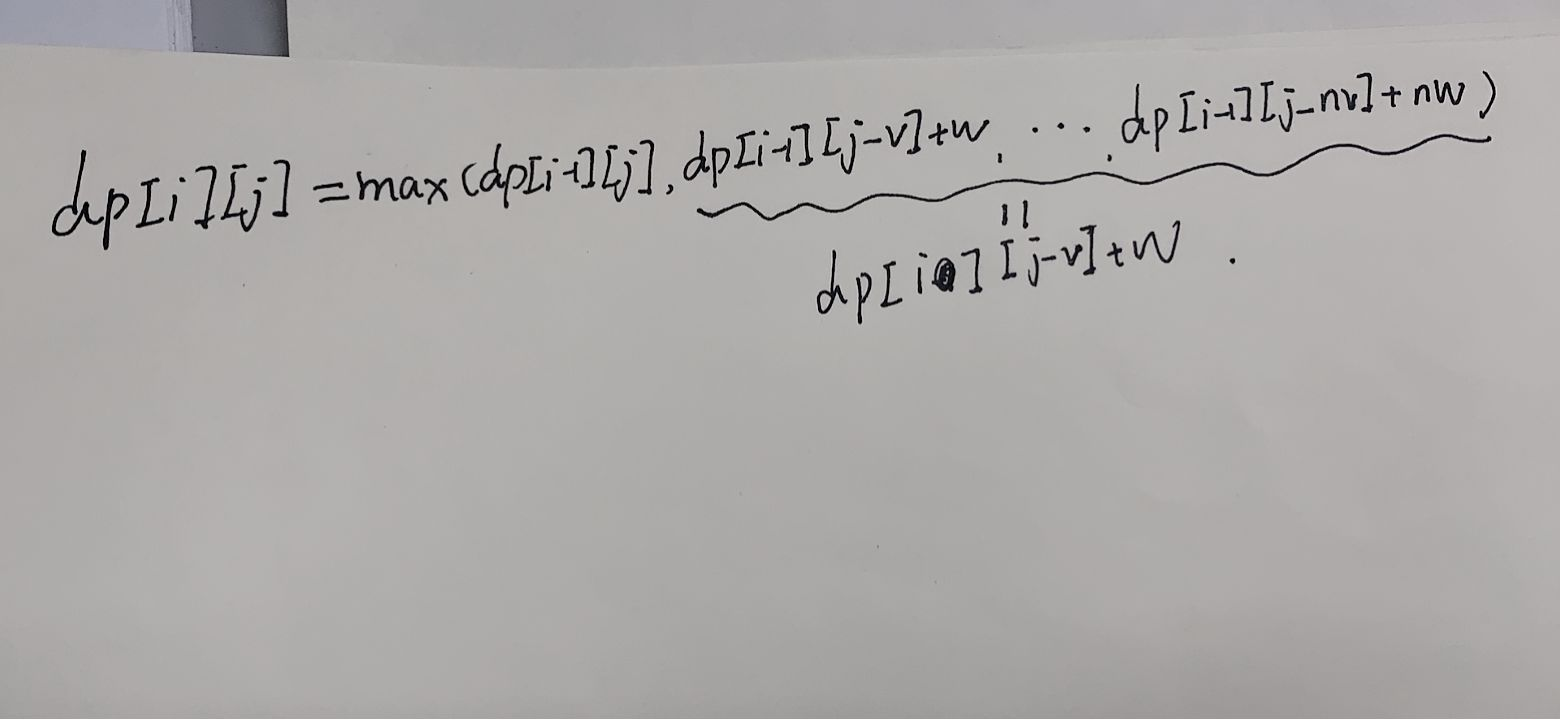
经过上面的公式,所以完全背包问题与0-1背包问题不同的地方就是第二个i-1变成了i
int knapsack(vector<int> weights, vector<int> values, int N, int W){
vector<vector<int>> dp(N+1, vector<int>(W+1, 0));
for(int i = 0; i < N; i++){
int w = weights[i-1], v = values[i-1];
for(int j = 0; j < M; j++){
if(j >= w){
dp[i][j] = max(dp[i-1][j], dp[i][j-v]+w);//只有这个地方不同
} else {
dp[i][j] = dp[i-1][j];
}
}
}
return dp[N][M];
}
空间压缩
这里的第二层循环选择正向的原因是dp[i][j] = max(dp[i-1][j], dp[i][j-v]+w),后面的部分需要取到当前层的dp[j-v],必须从小到大遍历。
int knapsack(vector<int> weights, vector<int> values, int N, int W){
vector<int> dp(W+1, 0);
for(int i = 0; i < N; i++){
int w = weights[i-1], v = values[i-1];
for(int j = w; j < M; j++){
dp[j] = max(dp[j], dp[j-w] + v);
}
}
return dp[N][M];
}
416. 分割等和子集
- 本题等价于0-1背包问题,设所有数字和为sum,如果sum为奇数则必定不可能存在两个子集和相等。
- 想要满足条件只需要满足能够从nums中找出一个子集和为sum/2即可,转化为0-1背包问题。
- 这题不需要考虑价值,因此我们只需要通过一个布尔值矩阵表示状态转移矩阵即可。
注意边界条件处理
class Solution { public: bool canPartition(vector<int>& nums) { int sum = accumulate(nums.begin(), nums.end(), 0), n = nums.size(); int target = sum/2; if(sum%2 != 0) return false; vector<vector<int>> dp(n+1, vector<int>(target+1)); dp[0][0] = true;//不要忘记边界条件处理 for(int i = 1; i <= n; i++){ for(int j = 0; j <= target; j++){ if(j < nums[i-1]){ dp[i][j] = dp[i-1][j]; } else { dp[i][j] = dp[i-1][j]||dp[i-1][j-nums[i-1]]; } } } return dp[n][target]; } };空间压缩
这里的第二层逆向的原因是dp[i][j] = dp[i-1][j]||dp[i-1][j-nums[i-1]]需要取到上一层的dp[j-nums[i-1]],为了避免破坏数据,必须要从大到小遍历。先遍历大的,这样就会自动使用上一层的dp数据。
class Solution { public: bool canPartition(vector<int>& nums) { int sum = accumulate(nums.begin(), nums.end(), 0), n = nums.size(); int target = sum/2; if(sum%2 != 0) return false; vector<bool> dp(target+1); dp[0] = true; for(int i = 1; i <= n; i++){ for(int j = target; j >= nums[i-1]; j--){ dp[j] = dp[j]||dp[j-nums[i-1]]; } } return dp[target]; } };474. 一和零(三维01背包问题)
看到这种选元素,有代价的问题,最大价值的问题就直接用01背包来写。
这是一个多维费用的0-1背包问题,有两个背包大小,0的数量和1的数量。
这里直接采用了压缩的写法class Solution { public: vector<int> getZerosOnes(string& str) {//得到0和1的数量 vector<int> zerosOnes(2); int length = str.length(); for (int i = 0; i < length; i++) { zerosOnes[str[i] - '0']++; } return zerosOnes; } int findMaxForm(vector<string>& strs, int m, int n) { int length = strs.size(); vector<vector<int>> dp(m + 1, vector<int>(n + 1)); for (int i = 0; i < length; i++) { vector<int>&& zerosOnes = getZerosOnes(strs[i]); int zeros = zerosOnes[0], ones = zerosOnes[1]; for (int j = m; j >= zeros; j--) { for (int k = n; k >= ones; k--) { dp[j][k] = max(dp[j][k], dp[j - zeros][k - ones] + 1);//与经典背包问题写法差不多 } } } return dp[m][n]; } }; //是用的01背包问题的思想494. 目标和(特殊模式的01背包问题)
这个很难一眼看出是不是背包问题,需要进行转化。

若上式成立,问题转化成在数组 \textit{nums}nums 中选取若干元素,使得这些元素之和等于 \textit{neg}neg,计算选取元素的方案数。我们可以使用动态规划的方法求解。
dp[i][j]表示在数组的前i个数中选取元素,是的这些元素之和等于j的方案数。假设数组的最终长度为n,则最终答案为dp[n][neg]
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for (int& num : nums) {
sum += num;
}
int diff = sum - target;
if (diff < 0 || diff % 2 != 0) {
return 0;
}
int n = nums.size(), neg = diff / 2;
vector<vector<int>> dp(n + 1, vector<int>(neg + 1));
dp[0][0] = 1;
for (int i = 1; i <= n; i++) {
int num = nums[i - 1];
for (int j = 0; j <= neg; j++) {
dp[i][j] = dp[i - 1][j];
if (j >= num) {
dp[i][j] += dp[i - 1][j - num];
}
}
}
return dp[n][neg];
}
};
优化之后
因为等式左边的始终是i的上一层循环,因此,可以优化掉i;又因为dp[i-1][j-num]是上一层循环较小的,因此,本次循环应该从大到小开始,避免影响dp的结果。
class Solution {
public:
int findTargetSumWays(vector<int>& nums, int target) {
int sum = 0;
for (int& num : nums) {
sum += num;
}
int diff = sum - target;
if (diff < 0 || diff % 2 != 0) {
return 0;
}
int neg = diff / 2;
vector<int> dp(neg + 1);
dp[0] = 1;
for (int& num : nums) {
for (int j = neg; j >= num; j--) {
dp[j] += dp[j - num];
}
}
return dp[neg];
}
};
322. 零钱兑换(完全背包问题)
注意边界,其他的与完全背包问题差不多。
class Solution { public: int coinChange(vector<int>& coins, int amount) { int n = coins.size(); vector<vector<int>> dp(n+1, vector<int>(amount+1, INT_MAX-1)); for(int i = 0; i <= n; i++){ dp[i][0] = 0; } for(int i = 1; i <= n; i++){ for(int j = 0; j <= amount; j++){ if(j >= coins[i-1]){ dp[i][j] = min(dp[i-1][j], dp[i][j-coins[i-1]] + 1); } else { dp[i][j] = dp[i-1][j]; } } } return dp[n][amount]==(INT_MAX-1) ? -1:dp[n][amount]; } };空间压缩
注意这里空间压缩,因为 dp[i][j-coins[i-1]],需要知道本层的dp[j-coins[i-1]]所以,从小到大遍历即可。
class Solution { public: int coinChange(vector<int>& coins, int amount) { int n = coins.size(); vector<int> dp(amount+1, INT_MAX-1); dp[0] = 0; for(int i = 1; i <= n; i++){ for(int j = coins[i-1]; j <= amount; j++){ dp[j] = min(dp[j], dp[j-coins[i-1]] + 1); } } return dp[amount]==(INT_MAX-1) ? -1:dp[amount]; } };871. 最低加油次数(另类背包问题)
加油站就相当于物品,加油的次数相当于容量,能行驶多远相当于价值。
dp[i][j]就相当于前i个加油站任你选,加油次数为j的情况下,能行驶的最大距离。
返回值就是看 这个行驶的最大距离是否大于target,如果大于则返回当前的j就是最少加油次数。
状态转移表达式:对于当前加油站i
- 加油 dp[i][j] = dp[i-1][j-1] + 当前加油站的油量,必要条件是dp[i-1][j-1]大于当前加油站的距离
- 不加油 dp[i][j] = dp[i-1][j]
以上两种情况的最大值就是dp[i][j]
class Solution { public: int minRefuelStops(int target, int startFuel, vector<vector<int>>& stations) { int n = stations.size(); vector<vector<long long>> dp(n+1, vector<long long>(n+1)); for(int i = 0; i <= n; i++) { dp[i][0] = startFuel; } for(int i = 1; i <= n; i++) { for(int j = 1; j <= n; j++) { if(dp[i-1][j-1] >= stations[i-1][0]){ dp[i][j] = max(dp[i-1][j-1] + stations[i-1][1], dp[i-1][j]); } else { dp[i][j] = dp[i-1][j]; } } } for(int j = 0; j <= n; j++) { if(dp[n][j] >= target) return j; } return -1; } };
字符串编辑问题
72. 编辑距离(多种情况)
- 这里的dp[i][j]的意思是,word1的前i个字符转换到word2的前j个字符所需要的最小次数。
- 分成三种情况,
- i=0时,直接就是j次
- j=0时,直接就是i次
- word1[i-1]==word2[j-1]时, dp[i][j] = min(dp[i-1][j-1], min(dp[i][j-1]+1, dp[i-1][j]+1))
word1[i-1]!=word2[j-1]时, dp[i][j] = min(dp[i-1][j-1]+1, min(dp[i][j-1]+1, dp[i-1][j]+1))
class Solution { public: int minDistance(string word1, string word2) { int m = word1.length(), n = word2.length(); vector<vector<int>> dp(m + 1, vector<int>(n + 1, INT_MAX)); for (int i = 0; i <= m; ++i) { for (int j = 0; j <= n; ++j) { if(i == 0){ dp[i][j] = j; } else if(j == 0){ dp[i][j] = i; } else{ dp[i][j] = min(dp[i-1][j-1] + ((word1[i-1] == word2[j-1])? 0: 1),min(dp[i-1][j] + 1, dp[i][j-1] + 1)); } } } return dp[m][n]; } };650. 只有两个键的键盘(和之前的分割问题很像)
dp[i]代表,到i个a最少需要多少次操作。
- 状态转移方程是
- 当i是由j粘贴a次的来的情况。dp[i] = min(dp[i], dp[j] + a);
- 返回来说i也可能是由a粘贴j次得来的,因此dp[i] = min(dp[i], dp[a] + j);
注意不可能出现jj>i的情况都是重复的情况,比如i为10,j为5,已经在前面j为2的情况出现了。因为jj>i的情况在j*j
普通操作
class Solution { public: int minSteps(int n) { vector<int> f(n + 1); for (int i = 2; i <= n; ++i) { f[i] = i; for (int j = 1; j <= i; ++j) { if (i % j == 0) { f[i] = min(f[i], f[j] + i / j); } } } return f[n]; } };降低复杂的操作
class Solution { public: int minSteps(int n) { vector<int> f(n + 1); for (int i = 2; i <= n; ++i) { f[i] = i; for (int j = 1; j * j <= i; ++j) { if (i % j == 0) { f[i] = min(f[i], f[j] + i / j); f[i] = min(f[i], f[i / j] + j); } } } return f[n]; } };10. 正则表达式匹配
区分好多种情况,分别是
当p[j-1] == ‘.’
- 当p[j-1] == 字符
- 当p[j-1] == ‘*’&&p[j-2] != s[i-1]&&p[j-2] != ‘.’
- 当p[j-1] == ‘*’&&能够匹配的情况
class Solution { public: bool isMatch(string s, string p) { int m = s.size(), n = p.size(); vector<vector<bool>> dp(m+1, vector<bool>(n+1, false)); dp[0][0] = true; for(int i = 1; i < n+1; i++){ if(p[i-1] == '*') dp[0][i] = dp[0][i-2]; } for(int i = 1; i < m+1; i++){ for(int j = 1; j < n+1; j++){ if(p[j-1] == '.'){ dp[i][j] = dp[i-1][j-1]; } else if(p[j-1] != '*'){ dp[i][j] = dp[i-1][j-1]&&p[j-1] == s[i-1]; } else if(p[j-2] != s[i-1]&&p[j-2] != '.'){ dp[i][j] = dp[i][j-2]; } else { dp[i][j] = dp[i][j-1] || dp[i-1][j] || dp[i][j-2]; } } } return dp[m][n]; } };股票交易
121. 买卖股票的最佳时机(仅限一次买卖)
动归写法
class Solution { public: int maxProfit(vector<int>& prices) { int n = prices.size(); if(n == 1) return 0; int a = prices[1] - prices[0]; int maxs = a; for(int i = 3; i <= n; i++){ a = max(prices[i-1] - prices[i-2],a + prices[i-1] - prices[i-2]); maxs = max (a, maxs); } return maxs > 0 ? maxs : 0; } };一次遍历
我们可以遍历一次数组,在每一个位置i时,记录i之前所有价格中的最低价格,然后将当前价格作为售出价格,查看当前是不是最大收益即可。class Solution { public: int maxProfit(vector<int>& prices) { int minprice = INT_MAX, maxprofit = 0; for (int price: prices) { minprice = min(price, minprice); maxprofit = max(maxprofit, price - minprice); } return maxprofit; } };最佳买卖股票时机不限次数
非dp写法
int maxpro(vector<int> prices){ int maxs = 0; for(int i = 1; i < prices.size(); ++i){ if(prices[i] > prices[i-1]){ maxs += prices[i] - prices[i-1]; } } return maxs; }dp写法
class Solution { public: int maxProfit(vector<int>& prices) { int n = prices.size(); vector<vector<int>> dp(n+1, vector<int>(2)); dp[1][1] = -prices[0]; for(int i = 2; i <= n; i++){ dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i-1]); dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i-1]); } return dp[n][0]; } };714. 买卖股票的最佳时机含手续费
相比上一题,多了个手续费
可以进行优化,因为i只与i-1有关class Solution { public: int maxProfit(vector<int>& prices, int fee) { int n = prices.size(); vector<vector<int>> dp(n+1, vector<int>(2)); dp[1][1] = -prices[0]; for(int i = 2; i <= n; i++){ dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i-1] - fee); dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i-1]); } return max(dp[n][0], dp[n][1]); } };309. 最佳买卖股票时机含冷冻期
增加一种冷冻期的状态。分为三种状态。持有股票、为冷冻期、不为冷冻期。 ```cpp class Solution { public: int maxProfit(vector& prices) {
} };if (prices.empty()) { return 0; } int n = prices.size(); // f[i][0]: 手上持有股票的最大收益 // f[i][1]: 手上不持有股票,并且处于冷冻期中的累计最大收益 // f[i][2]: 手上不持有股票,并且不在冷冻期中的累计最大收益 vector<vector<int>> f(n, vector<int>(3)); f[0][0] = -prices[0]; for (int i = 1; i < n; ++i) { f[i][0] = max(f[i - 1][0], f[i - 1][2] - prices[i]); f[i][1] = f[i - 1][0] + prices[i]; f[i][2] = max(f[i - 1][1], f[i - 1][2]); } return max(f[n - 1][1], f[n - 1][2]);
<a name="uTLiq"></a>
### [188. 买卖股票的最佳时机 IV](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-iv/)(指定次数)
<a name="Liw4B"></a>
#### 状态转移方程
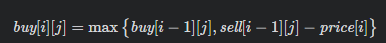<br />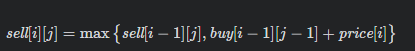
<a name="UVkc7"></a>
#### 边界条件
考虑将buy[0][i]以及sell[0][j]设置为边界<br /><br />使用sell和buy分别储存手上没有股票和有股票的情况<br /><br />
<a name="aawGH"></a>
#### 使用三维vector
```cpp
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
if (prices.empty()) {
return 0;
}
int n = prices.size(), res = 0;
k = min(k, n / 2);
vector<vector<vector<int>>> dp(n, vector<vector<int>>(k + 1, vector<int> (2)));
dp[0][0][1] = -prices[0];
dp[0][0][0] = 0;
for (int i = 1; i <= k; ++i) {
dp[0][i][0] = dp[0][i][1] = INT_MIN / 2;
}
for (int i = 1; i < n; ++i) {
dp[i][0][1] = max(dp[i - 1][0][1], - prices[i]);
for (int j = 1; j <= k; ++j) {
dp[i][j][1] = max(dp[i - 1][j][1], dp[i - 1][j][0] - prices[i]);
dp[i][j][0] = max(dp[i - 1][j][0], dp[i - 1][j - 1][1] + prices[i]);
res = max(dp[i][j][0], res);
}
}
return res;
}
};
使用sell以及buy
class Solution {
public:
int maxProfit(int k, vector<int>& prices) {
if (prices.empty()) {
return 0;
}
int n = prices.size();
k = min(k, n / 2);
vector<vector<int>> buy(n, vector<int>(k + 1));
vector<vector<int>> sell(n, vector<int>(k + 1));
buy[0][0] = -prices[0];
sell[0][0] = 0;
for (int i = 1; i <= k; ++i) {
buy[0][i] = sell[0][i] = INT_MIN / 2;
}
for (int i = 1; i < n; ++i) {
buy[i][0] = max(buy[i - 1][0], - prices[i]);
for (int j = 1; j <= k; ++j) {
buy[i][j] = max(buy[i - 1][j], sell[i - 1][j] - prices[i]);
sell[i][j] = max(sell[i - 1][j], buy[i - 1][j - 1] + prices[i]);
}
}
return *max_element(sell[n - 1].begin(), sell[n - 1].end());
}
};
复杂度
无论是时间复杂度还是空间复杂度,buy和sell都与vector一样。但是实际性能却远远超过。最好还是使用buy和sell
状态压缩
1494. 并行课程 II(华为机式)
这题使用拓扑排序是错误的,同样深度时无法判断优先级。
只能使用状态压缩
class Solution {
public:
int minNumberOfSemesters(int n, vector<vector<int>>& relations, int k) {
vector<int> prerequisite(n, 0);
for (const auto& pair : relations) {
int pre = pair[0] - 1;
int after = pair[1] - 1;
// 举例:prerequisite[1] = 0110 表示1的先修课为2和3
prerequisite[after] |= 1<<pre;
}
int totalState = 1 << n;
vector<int> dp(totalState, 16);
// 0为不需要上任何课的状态,因此不需要学期
dp[0] = 0;
vector<int> cnt(totalState);
cnt[0] = 0;
// 小技巧,计算每个数字的二进制数中,1的个数
for (int i = 1; i < totalState; ++i) {
cnt[i] = cnt[i>>1] + (i&1);
}
// taken表示已经上过的课,假设taken = 0111,表示课程1 2 3已经上过了
for (int taken = 0; taken < totalState; ++taken) {
if (dp[taken] > n) continue;
int cur = 0;
// 在上过taken的基础上,还有哪些课可以上,要满足两个条件
// 1. ((taken & (1 << j)) == 0) 表示这个课在taken中没上过
// 2. ((prerequisite[j] & taken) == prerequisite[j]) 表示这个课的先修课已经上完了
for (int j = 0; j < n; ++j) {
if (((taken & (1 << j)) == 0) && ((prerequisite[j] & taken) == prerequisite[j])) {
// 存这学期可以上的课,注意,可以上不代表一定要上,也不一定要上满,这题的本质是NPC问题,任何贪心的思想都是错的,选择cur中的课来上的这个操作,用下面枚举子集的方法实现
cur |= (1 << j);
}
}
// 枚举cur的子集,比如cur = 111,它的子mask集合就是{111, 110, 101 011, 100, 010, 001}
for (int subMask = cur; subMask != 0; subMask = subMask-1 & cur) {
// 这学期上的课的数量不能超过k
if (cnt[subMask] <= k) {
// 之前上完taken,这学期再上subMask,看看会不会更好
dp[taken|subMask] = min(dp[taken|subMask], dp[taken] + 1);
}
}
}
return dp[totalState - 1];
}
};
特殊情况
552学生出勤记录Ⅱ
这一题的动态规划非常特别值得深思,这一题的动态规划在每一个阶段都有几种情况,需要分别考虑这些情况。
class Solution {
int MOD = 1000000007;
public int checkRecord(int n) {
long[][] dp = new long[2][3];
// 初始值
dp[0][0] = 1;
dp[1][0] = 1;
dp[0][1] = 1;
for (int i = 1; i < n; i++) {
long[][] newDp = new long[2][3];
newDp[0][0] = (dp[0][0] + dp[0][1] + dp[0][2]) % MOD;
// 把方法三中间两个一样的状态合并为一行
newDp[1][0] = (dp[1][0] + dp[1][1] + dp[1][2] + dp[0][0] + dp[0][1] + dp[0][2]) % MOD;
newDp[0][1] = dp[0][0];
newDp[0][2] = dp[0][1];
newDp[1][1] = dp[1][0];
newDp[1][2] = dp[1][1];
dp = newDp;
}
long ans = 0;
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 3; j++) {
ans = (ans + dp[i][j]) % MOD;
}
}
return (int) ans;
}
}
1218. 最长定差子序列(dp+哈希)
dfs(超时)
使用dfs时间不复杂度不符合要求。
class Solution {
public:
int ret = 0;
int longestSubsequence(vector<int>& arr, int difference) {
int n = arr.size();
vector<bool> flags(n);
for(int i = 0; i < n; i++){
if(!flags[i])
dfs(arr, flags, difference, i, 1);
}
return ret;
}
void dfs(vector<int> &arr,vector<bool> &flags, int difference, int idx, int val){
ret = max(ret, val);
flags[idx] = true;
for(int i = idx+1; i < arr.size(); i++){
if((arr[i] - arr[idx]) == difference){
dfs(arr, flags, difference, i, val+1);
}
}
}
};
官解
雀食非常巧妙,直接用哈希表来构建dp数组,实现复杂度为1的数据查找。
- 这一题有一个思考点,在寻找子集之间的关系时,两个子集不一定时严格相邻的。
- 用值来作为索引,像这种不是以数组下标作为子集的索引的,可以考虑以哈希表的key作为索引。
class Solution { public: int longestSubsequence(vector<int> &arr, int difference) { int ans = 0; unordered_map<int, int> dp; for (int v: arr) { dp[v] = dp[v - difference] + 1; ans = max(ans, dp[v]); } return ans; } };总结
为什么dp复杂度为n,是因为dp将这个问题化为了只有一条路径
而dfs相当于多条路径的寻找,有多个分支,而dp只有一条分支。375. 猜数字大小 II(重点)
这一题的思想非常巧妙,我是真的没有想到用dp来写。
为了将支付的金额最小化,除了需要将每次支付的金额控制在较低值以外,还需要在猜数字的过程中缩小所选数字的范围。当猜了数字 xx 并且猜错时,会知道 x 比所选数字大还是小。如果 x 比所选数字大,则任何比 x 大的数字一定都比所选数字大,因此应该在比 x 小的数字中继续猜数字。如果 x 比所选数字小,同理可知应该在比 x 大的数字中继续猜数字。
用 f(i, j)表示在范围 [i, j]内确保胜利的最少金额,目标是计算f(1, n)。
假设第一次猜的数字是 x 并且猜错,则需要支付金额 x,当 x 大于所选数字时,为了确保胜利还需要支付的金额是 f(1, x - 1),当 x 小于所选数字时,为了确保胜利还需要支付的金额是 f(x + 1, n)。为了在任何情况下都能确保胜利,应考虑最坏情况,计算f(1,n) 时应取上述两者的最大值:f(1, n) = x + max(f(1, x - 1), f(x + 1, n))。
为了将确保胜利的金额最小化,需要遍历从 1 到 n 的所有可能的 x,使得f(1,n) 的值最小:
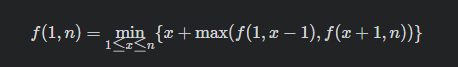
由于f(1,x−1) 和 f(x+1,n) 都是比原始问题f(1,n) 规模更小的问题,因此可以使用动态规划的方法求解。
动态规划的状态为f(i,j),表示在范围 [i, j][i,j] 内确保胜利的最少金额。
当i=j 时范围 [i, j]只包含 11 个数字,所选数字一定是范围内的唯一的数字,不存在猜错的情况,因此 f(i, j) = 0;当 i > j 时范围 [i,j] 不存在,因此 f(i, j) = 0。综合上述两种情况可知,动态规划的边界情况是:当 i≥j 时,f(i,j)=0。
当 i < j时,在范围 [i, j] 内第一次猜的数字可能是该范围内的任何一个数字。在第一次猜的数字是 k 的情况(i≤k≤j),在范围 [i, j][i,j] 内确保胜利的最少金额是 k + max(f(i, k - 1), f(k + 1, j))。需要遍历全部可能的 k 找到在范围 [i, j] 内确保胜利的最少金额,因此状态转移方程如下: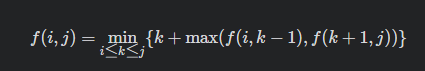
由于状态转移方程为根据规模小的子问题计算规模大的子问题,因此计算子问题的顺序为先计算规模小的子问题,后计算规模大的子问题,需要注意循环遍历的方向。
区间遍历从前往后的写法
class Solution {
public:
int getMoneyAmount(int n) {
vector<vector<int>> f(n+1,vector<int>(n+1));
for (int j = 2; j <= n; j++) {
for (int i = j - 1; i >= 1; i--) {
int minCost = INT_MAX;
for (int k = i; k < j; k++) {//循环所有可能
int cost = k + max(f[i][k - 1], f[k + 1][j]);
minCost = min(minCost, cost);
}
f[i][j] = minCost;
}
}
return f[1][n];
}
};
区间遍历从后往前的写法
class Solution {
public:
int getMoneyAmount(int n) {
vector<vector<int>> f(n+1,vector<int>(n+1));
for (int i = n - 1; i >= 1; i--) {
for (int j = i + 1; j <= n; j++) {
int minCost = INT_MAX;
for (int k = i; k < j; k++) {//循环所有可能
int cost = k + max(f[i][k - 1], f[k + 1][j]);
minCost = min(minCost, cost);
}
f[i][j] = minCost;
}
}
return f[1][n];
}
};
6109. 知道秘密的人数(周赛题目)

class Solution {
const int MOD = 1e9 + 7;
public:
int peopleAwareOfSecret(int n, int delay, int forget) {
int cnt_a = 0;//A类人,知道秘密,但是不能分享
int f[n]; //B类人,知道秘密,可以分享。表示第i天的B类人数。
memset(f, 0, sizeof(f));
f[0] = 1;
for (int i = 0; i < n; ++i) {//当前天数
if (i + delay >= n) cnt_a = (cnt_a + f[i]) % MOD;//都是A类人
for (int j = i + delay; j < min(i + forget, n); ++j)
f[j] = (f[j] + f[i]) % MOD;
}
return (cnt_a + f[n - 1]) % MOD;//最终结果就是A类人以及B类人之和。
}
};

