图论

二分图

785. 判断二分图

• 利用队列和广度优先搜索，对未染色的节点进行染色，并且检查是否有颜色相同的相邻节点存在。

• 用0代表未检查的节点，用1和2表示两种不同的颜色。

  class Solution {
  public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();//代表有多少点
        vector<int> color(n, 0);//每个点都有一个颜色，0代表没有遍历到，1和2代表两种颜色。
        queue<int> q;
        for(int i = 0; i < n ; i++){
            if(color[i] == 0){
                q.push(i);
                color[i] = 1;
            }
            while(!q.empty()){
                int node = q.front();//node是当前点
                q.pop();
                for(int a : graph[node]){//和当前节点相连的节点都入队
                    if(color[a] == 0){//如果a还没有遍历过
                        q.push(a);
                        color[a] = color[node]== 1 ? 2:1; 
                    } 
                    else if(color[a] == color[node]){
                        return false;
                    }
                }
            }
        }
        return true;
    }
  };

  拓扑排序

  给定一个包含n个节点的有向图G，我们给出它的节点编号的一种排列，如果满足：
  对于图G的任意一条有向边（u，v），u在排列中都出现在v的前面，那么称该排列是图G的拓扑排列。
  根据上述定义可以得出两个结论：

• 如果图G中存在环，那么图G不存在拓扑排序。这是因为假设途中存在环x1,x2,⋯,xn,x1，那么x1在排列中必须出现在xn的前面，但xn同时也必须出现在x1的前面，自相矛盾。

• 如果图G是有向无环图，那么它的拓扑排序可能不止一种。举一个极端例子，如果图G值包含n个节点却没有边，那么任意一种编号的排列都可以作为拓扑排序。

207. 课程表（经典拓扑排序）

• 通过拓扑排序来看是否能通过所有课程
• 我们将每一门课看成一个节点
• 如果想要学习A之前必须完成课程B，那么我们从B到A连接一条有向边。这样以来，在拓扑排序中，B一定要出现在A的前面。
• edges为出度的集合，代表这个课程是多少个课程的前置。indeg为入度，代表这个课程需要多少个前置。

class Solution {
private:
    vector<vector<int>> edges;
    vector<int> indeg;
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        edges.resize(numCourses);
        indeg.resize(numCourses);
        for (const auto& info: prerequisites) {
            edges[info[1]].push_back(info[0]);
            ++indeg[info[0]];
        }
        queue<int> q;
        for (int i = 0; i < numCourses; ++i) {
            if (indeg[i] == 0) {
                q.push(i);
            }
        }
        int visited = 0;
        while (!q.empty()) {
            ++visited;
            int u = q.front();
            q.pop();
            for (int v: edges[u]) {
                --indeg[v];
                if (indeg[v] == 0) {
                    q.push(v);
                }
            }
        }
        return visited == numCourses;
    }
};

210. 课程表 II

• 这一题与上一题不同的是，返回的是上课程的顺序。

  class Solution {
  public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph(numCourses,vector<int>());//建图
        vector<int> indegree(numCourses,0);//入度
        queue<int> q;
        vector<int> res;
        for(int i = 0; i < prerequisites.size(); i++){
            graph[prerequisites[i][1]].push_back(prerequisites[i][0]);
            ++indegree[prerequisites[i][0]];
        }
        for(int i = 0; i < indegree.size(); i++){
            if(!indegree[i])//入度为零的先入队
            q.push(i);
        }
        while(!q.empty()){
            int u = q.front();
            res.push_back(u);
            q.pop();
            for(auto v : graph[u]){
                indegree[v]--;
                if(!indegree[v]){//入度为零入队
                    q.push(v);
                }
            }
        }
        for(int i = 0; i < indegree.size(); i++){
            if(indegree[i])//如果存在课程入度不为0，则直接返回空vector
            return vector<int>();
        }
        return res;
    }
  };

  310. 最小高度树（拓扑排序变形）

• 本题其实就是拓扑排序的变式。就是不断缩小图，直至剩下1、2个点，return。

• 本题为无向图，所以删除的点是入度为1的点
• 本题不能一个个的删除入度为1的点，而应该在一个循环中，一次性删除入度为1的点，使得以同样的速度缩小图，直至剩下的点。

证明：其实这种方法只能正针对有树特征的图（无环结构），同时答案至多有两个解。 答案至多有两个解是应该可以证明的，下面是我不严谨的证法：这个图是可以进行等效剪枝的（去掉距离相同或者更短的枝干），最终可以将图化简为一条链，链长度为偶数则有两个解，链长度为奇数则有一个解。

class Solution {
private:
    // 找最小高度，最短路径想到BFS
    // 两端烧香求中点
public:
    vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
        if (n == 1) return {0};
        vector<int> res;        
        // 每个节点的度数
        vector<int> degree(n);
        // 建立无向邻接图
        vector<vector<int>> map(n);
        for (int i = 0; i < edges.size(); i++) {
            int v1 = edges[i][0];
            int v2 = edges[i][1];
            degree[v1]++;
            degree[v2]++;
            map[v1].push_back(v2);
            map[v2].push_back(v1);
        }
        // 把度为1的节点入队
        queue<int> q;
        for (int i = 0; i < n; i++) {
            if (degree[i] == 1) 
            q.push(i);
        }
        // BFS
        while (!q.empty()) {
            // 清理当前层的节点
            res.clear();
            int size = q.size();
            while (size--) {
                int cur = q.front();
                q.pop();
                res.push_back(cur);
                // 减小对应度数
                degree[cur]--;
                for (auto i : map[cur]) {
                    degree[i]--;
                    if (degree[i] == 1) {
                        q.push(i);
                    }
                }
            }
        }     
        return res;
    }
};

279. 完全平方数（bfs+建图）

建图：

• 根据bfs一层一层建图

• 记忆化来剪枝

  class Solution {
  public:
    int numSquares(int n) {
         //图论，从n到0，每个数字表示一个节点，如果两个数字之间此昂差一个完全平方数，则连接一条边，求最短路径(无权图))     
         assert(n>0);
         queue<int> q;//分别存储n和需要走几步到达该数
         q.push(n);
         int res = 0;
         vector<bool> visited(n+1,false);//排除冗余的节点
         visited[n]=true;
         while(!q.empty()){
            int size = q.size();
             while(size--){
                 int num = q.front();
                 q.pop();
                 if(num == 0) return res;
                 for(int i = 1;num-i*i>=0; i++){
                     if(!visited[num-i*i]){
                         visited[num-i*i]=true;
                         q.push(num-i*i);
                     }
                 }
             }
             res++;
         }
         throw invalid_argument("No Solution.");
    }
  };

  动规：

  根据子集与子集之间的关系来计算父集。
  状态转移方程：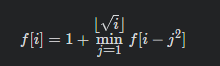
  

  class Solution {
  public:
    int numSquares(int n) {
        vector<int> dp(n+1,INT_MAX);
        dp[0]=0;
        for(int i =1;i<=n;i++){
            for(int j = 1;j*j<=i;j++){
                dp[i] = min(dp[i],dp[i-j*j]+1);
            }
        }
        return dp[n];
    }
  };

  剑指 Offer II 114. 外星文字典

  class Solution {
  public:
    string alienOrder(vector<string>& words) {
        unordered_map<char, unordered_set<char>> graph;//这里应该是每个字母的后面的字母。
        unordered_map<char, int> inDegress;
        // 建图
        for (auto& word : words) {
            for (auto& ch : word) {
                if (!graph.count(ch)) {
                    graph[ch] = {};
                } 
                if (!inDegress.count(ch)) {
                    inDegress[ch] = 0;
                }
            }
        }
        // 计算邻接表和入度
        for (int i = 1; i < words.size(); ++i) {//通过对比相邻的两个字符串来计算入度。
            int j = 0;
            int len = min(words[i - 1].size(), words[i].size());
            for (; j < len; ++j) {
                char ch1 = words[i - 1][j];
                char ch2 = words[i][j];
                if (ch1 != ch2) {//出现不等直接break，因为ch1排序在ch2之前。
                    if (!graph[ch1].count(ch2)) {
                        graph[ch1].insert(ch2);
                        inDegress[ch2]++;
                    }
                    break;
                }
            }
            // 特殊判断
            //如果后面的单词是前面单词的前缀，并且后面的单词小于前面的单词的长度。直接返回空即可
            if (j == len && words[i - 1].size() > words[i].size()) {//如果是无效字母顺序
                return {};
            }
        }
        string ret{""};
        queue<char> que;
        // 入度为 0 的点，先入队
        for (auto& d : inDegress) {
            if (d.second == 0) {
                que.push(d.first);
            }
        }
        // BFS，进行搜索
        while (!que.empty()) {
            char ch = que.front();
            que.pop();
            ret.push_back(ch);
            for (auto& c : graph[ch]) {
                inDegress[c]--;
                if (inDegress[c] == 0) {
                    que.push(c);
                }
            }
        }
        if (ret.size() != inDegress.size()) {//存在字符的入度无法为0，非法
            return "";
        }
        return ret;
    }
  };

  433. 最小基因变化（双向bfs+常看）

  
  

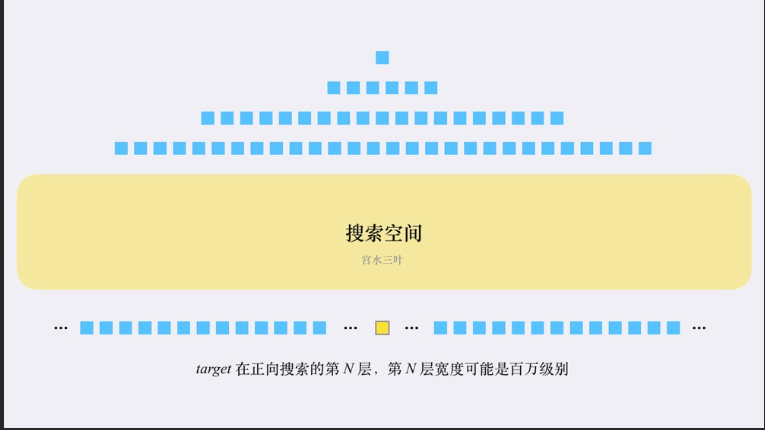
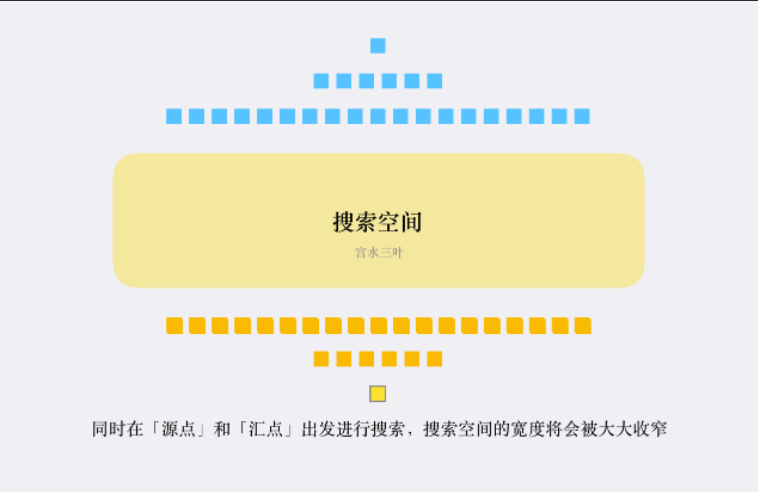
• 这里分别标记从前往后为1，从后往前为2，如果标记为3的话就代表前和后都遍历到了。就是我们要的答案。

  class Solution {
  public:
    // 解法2：双向bfs
    int minMutation(string start, string end, vector<string>& bank) {
        // 1：建立hashmap表，顺便去掉重复元素
        unordered_map<string,int> mp;
        for(const auto& b:bank)mp[b]=0;
        // 2：排除极端情况，end不在基因库中
        if(mp.count(end)==0)return -1;
        // 3：bfs的初始化工作
        queue<string> q1({start}),q2({end});// 前向队列，后向队列
        int step=0;
        const char table[4]={'A','C','G','T'};// 基因的字符
        // 或1表示前向队列由前往后遍历，或2表示后向队列由后向前遍历，每次我们选用较小的队列进行遍历
        for(mp[start]|=1,mp[end]|=2;q1.size()&&q2.size();++step)//每遍历完一次，步长+1
        {
            bool first=q1.size()<q2.size();
            //注意后面使用引用来写的，这很重要！
            queue<string> &q=first?q1:q2;// 选择较小的队列进行遍历节约时间，两个队列轮询。
            int flag=first?1:2;// 此次遍历的方式
            for(int n=q.size();n--;q.pop()){
                string& temp=q.front();
                if(mp[temp]==3)return step;// 两个队列碰头，返回步长，这里是即与1或了，也与2或了。就代表两个方向出现了公共点。
                for(int i=0;i<temp.size();++i){//对字符串中的每一个字符，都可以转换成table中的别的字符。
                    for(int j=0;j<4;++j){
                        string s=temp;
                        if(s[i]==table[j]) continue;// 重复字符，跳出循环，寻找下一个字符
                        s[i]=table[j];
                        if(mp.count(s)==0||mp[s]==flag) continue;// 该单词不在基因库中，或该单词已经被遍历过了，跳出循环，寻找下一个单词
                        mp[s]|=flag;// 标记该单词已经被遍历过了
                        q.push(s);
                    }
                }
            }
        }
        return -1;
    }
  };