排序算法总结

复杂度分析

线性时间排序

计数排序

基数排序

桶排序

将数据放在几个有序的桶内，将每个桶内的数据进行排序，最后有序地将每个桶中的数据从小到大依次取出。
我们举个例子来帮助理解，现在有一个数组：20，33，42，12，65，42，98，76，14，88，53，77。运用桶排序，假设我们划分5个桶，分别装0-19，20-39，40-59，60-79，80-99的数，再将每个桶中的数进行排序，可以运用快排，最后再将一个一个桶里的数依次取出，即完成排序。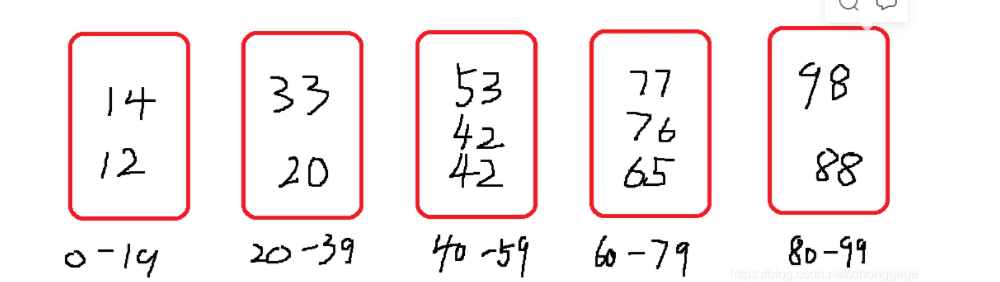

为什么桶排序的复杂度是n呢：

如果n与桶大小的平方中有一定的线性关系，也就是说m随着n的增长而增长，则n/m就是一个常数，则nlog(n/m)的增长速率可以看作是O(n)；

缺点

数组随机化的算法

我们知道快速排序的性能和「划分」出的子数组的长度密切相关。直观地理解如果每次规模为 n 的问题我们都划分成 1 和 n−1，每次递归的时候又向 n−1 的集合中递归，这种情况是最坏的，时间代价是 O(n ^ 2）
我们可以引入随机化来加速这个过程，它的时间代价的期望是 O(n)，证明过程可以参考「《算法导论》9.2：期望为线性的选择算法」。

srand(time(0));//随机数种子随时间变化。
void randomsort(vector<int>& nums){
        for(int i = 0; i < nums.size(); i++){
            int j = rand()%nums.size();
            swap(nums[i], nums[j]);
        }
}

快速排序（quick sort）

采用左闭右闭得二分写法

• 核心思想就是每次递归保证比他大得数都在后面，比他小得数都在前面。
• 必须保证先右后左，先q后p，先last后firtst

• 因为已知nums[l] = key，但是nums[r]就不敢保证了。

  void quick_sort(vector<int>& nums, int l ,int r, int target) {
        if(l >= r || flag) {
            return;
        }
        swap(nums[l], nums[rand()%(r-l)+l]);//随机化，随机取一个元素和头部元素交换。
        int tmp = nums[l], i = l, j = r-1;
        while(i < j) {
            while(i < j&&nums[j] >= tmp) {//这里顺序不能变，必须先遍历右边才行，因为
                j--;
            }
            while(i < j&&nums[i] <= tmp) {
                i++;
            }
            swap(nums[i], nums[j]);
        }
        swap(nums[l], nums[i]);
        quick_sort(nums, l,  i,  target);
        quick_sort(nums, i+1,  r,  target);
    }

  归并排序（merge sort）

  分治法的思想，先分后治

• 将一个大数组分成一个个小数对然后排序，然后合并

• 这里需要注意区间的选择

  void merge_sort(vector<int>& nums, int l, int r, vec<int> &temp){
    if(l + 1 >= r) return ;
    int m = l + (r-l)/2;
    merge_sort(nums, l, m, temp);
    merge_sort(nums, m, r, temp);
    int p = l, q = m, i = l;
    while(p < m || q < r){//只有两个都错才结束循环
        if(q >= r ||(p < m&&nums[p] <= nums[q])){
            temp[i++] = nums[p++];
        } else {
            temp[i++] = nums[q++];
        }
    }
    for(i = l; i < r; i++){
        nums[i] = temp[i];
    }
  }

  插入排序（Insertion sort）

  延申是希尔排序
  每一步将待排序的数据插入到前面已经排好序的序列中
  每一个二级循环都始终保持数组是从小到大。

  void insetion_sort(vector<int>& nums, int n){
    for(int i = 0; i < n; ++i){
        for(int j = i; j > 0&&nums[j] < nums[j-1]; j--){
            swap(nums[j], nums[j-1]);
        }
    }
  }

  冒泡排序（Bubble sort）

  每次都把最小的放到前面或者把最大的放到后面，通过两层循环来实现。

  void bubble_sort(vector<int>&nums, int n){
    bool swapped;
    for(int i = 1; i < n; i++){
        swapped = false;
        for(int j = 1; j < n-i+1; ++j){
            if(nums[j] < nums[j-1]){
                swap(nums[j],nums[j-1]);
                swapped = true;
            }
        }
        if(!swapped){
        break;
        }
    }
  }

  选择排序（Selection sort）

  与冒泡排序的区别是：交换的次数不同。冒泡排序每次比较就要立刻交换，而选择排序是被未排序最小的数的下标找出来与相应位置上的元素交换。选择排序交换次数较少。
  但是选择排序不稳定，会破坏相同元素相对位置的前后顺序。
  比如 58529，这个数组，第一次会将5和2调换位置，这样就破坏了两个5的相对顺序。

  void selection_sort(vector<int>& nums, int n){
    int mid;
    for(int i = 0; i < n-1; i++){
        mid = i;
        for(int j = i + 1; j < n; j++){
            if(nums[j] < nums[mid]){
                mid = j;
            }
        }
        swap(nums[mid], nums[i]);
    }
  }

  优先队列

  堆排序（heap sort）

• 堆是一个数组，可以被看作是一个完全二叉树

• 左右节为2i+1和2i+2，父节点为(i-1)/2
• 主要有三个操作，分别是max_heapify维护大根堆，每次将父节点设置为最大的一个，然后继续维护。
• adjust操作用来构建大顶堆。
• heapsort的后半部分操作就是每次都把堆顶的数字放到末尾，然后排除末尾进行adjust；

#include <iostream>
#include <vector>
using namespace std;
vector<int> heap = {8, 1, 14, 3, 21, 5, 7, 10};
// 上浮
void swim(int pos) {
    while (pos > 0 && heap[(pos-1)/2] < heap[pos]) {
        swap(heap[(pos-1)/2], heap[pos]);
        pos = (pos-1)/2;
    }
}
// 下沉
void sink(int pos) {
    while (2 * pos < heap.size()) {
        int i = 2 * pos + 1;
        if (i < heap.size() && heap[i] < heap[i+1]) ++i;//选子节点较大的一个
        if (heap[pos] >= heap[i]) break;//如果父节点大于较大的子节点则无事发生
        swap(heap[pos], heap[i]);//否则 交换值
        pos = i;//下次用的父节点，为交换的子节点
    }
}
void adjust(vector<int> &heap, int len, int index)
{
    int left = 2*index + 1; // index的左子节点
    int right = 2*index + 2;// index的右子节点，在算法导论的下标为2i和2i+1因为算法导论书中下标是从1开始的。
    int maxIdx = index;
    if(left<len && heap[left] > heap[maxIdx])     maxIdx = left;
    if(right<len && heap[right] > heap[maxIdx])     maxIdx = right;//这就是从根左右中选出最大的
    if(maxIdx != index)
    {
        swap(heap[maxIdx], heap[index]);
        adjust(heap, len, maxIdx);//递归的维护所有子堆
    }
}
// 获得最大值
int top() {
    return heap[0];
}
// 插入任意值：把新的数字放在最后一位，然后上浮
void push(int k) {
    heap.push_back(k);
    swim(heap.size() - 1);
}
// 删除最大值：把最后一个数字挪到开头，然后下沉
void pop() {
    heap[0] = heap.back();
    heap.pop_back();
    sink(0);
}
// 堆排序
void heapsort(vector<int> &heap, int size)
{
    // 构建大根堆（从最后一个非叶子节点向上）
    for(int i=size/2 - 1; i >= 0; i--)//n/2往后的节点都是叶子节点，先不管。
    {
        adjust(heap, size, i);
    }
    // 调整大根堆
    // for(int i = size - 1; i >= 1; i--)
    // {
    //     swap(heap[0], heap[i]);           // 将当前最大的放置到数组末尾
    //     adjust(heap, i, 0);              // 将未完成排序的部分继续进行堆排序
    //                                     //这一部分正常构建大根堆是没有的，因为不用保证左右子节点大小，堆排序加上这个部分。顺序是从小打到大
    // }
}
int main()
{
    heapsort(heap, heap.size());
    push(100);
    for(int i=0;i<heap.size();i++)
    {
        cout<<heap[i]<<endl;
    }
    return 0;
}

桶排序